Прямая на плоскости
Всякая прямая линия определяется в заданной прямоугольной декартовой системе координат Оху уравнением первой степени относительно переменных х и у.
Ах + Ву + С= 0 (1)
общее уравнение прямой, где А и В - координаты одного из нормальных векторов этой прямой.
|
(2)
каноническое уравнение прямой, где (х0,у0) - координаты точки, через которую проходит прямая, l и т- координаты направляющего вектора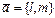 
.
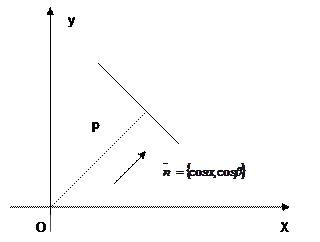
xCosa+yCosβ-p = 0 (3)
нормированное уравнение прямой, где Cosa,Cosβ - координаты единичного вектора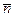 
нормали прямой (он направлен из начала координат к прямой), р - расстояние прямой от начала координат 
.
Из уравнений (1)-(3) могут быть получены удобные в геометрическом смысле уравнения:
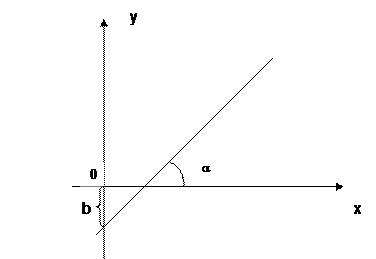
у = кх + b (4)
уравнение с угловым коэффициентом к = tga, α - угол наклона прямой к оси Ох, b - величина отрезка, отсекаемого на оси Оу.
(5)
уравнение прямой, проходящей через две данные точки (х1,у1) и (х2 ,у2).
(6)
параметрические уравнения прямой, проходящей через точку (хо ,уо) в направлении вектора 
= {1,т).
(7)
уравнение прямой «в отрезках», где а и b величины отрезков отсекаемых прямой на осях ох и оу соответственно.
Взаимное расположение двух прямых, заданных уравнениями (1),(2),(3), вполне определяется взаимным расположением векторов с ними связанных, поэтому условия параллельности, ортогональности и угол между прямыми получены из соответствующих условий для векторов. Для прямых, заданных уравнениями вида (4), выпишем эти условия. Если y=k1х + b1 и у = к2х + Ь2 уравнения этих прямых, то
k1 =k2 –условие параллельности, (8)
k1×k 2=-1 –условие перпендикулярности, (9)
-тангенс угла между прямыми (10)
Если дана прямая общим уравнением Aх + Ву + С=О, то его можно нормировать умножением на нормирующий множитель
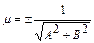, (11)
где знак выбирается противоположным знаку свободного члена С из общего уравнения
μАх + μBу + μC = 0
Нормированное уравнение позволяет получить отклонение δ и расстояние d для данной точки М0(х0,у0) от прямой по формуле δ = х0 cosα + у0 cosβ - ρ,
. (12)
Пример 1. Найти угол между прямыми
.
Решение.
,
тогда другой угол между прямыми 135°.
Пример 2. Найти проекцию точки Мо(4,9) на прямую, проходящую через точки М1(3,1) и М2(5,2).
Решение. Найдем уравнение прямой М1М2 по формуле (5)
,
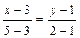откуда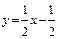 
. Ищем уравнение перпендикуляра к этой прямой, проходящего через точку Мо в виде (4). Пользуясь условием перпендикулярности кгк1 =-1, найдем 
. Так как координаты Мо должны удовлетворять искомому уравнению, то в уравнение у=-2x+b подставим координаты Мо: 9 =-2×4+b.
Получим b= 17. Точка пересечения заданной прямой и этого перпендикуляра даст проекцию Мо на данную прямую.
Решим систему:
.
Получим х = 7,у = 3.
Пример 3. Найти расстояние между параллельными прямыми
у=2х-З и у=2х + 5.
Решение. На первой прямой найдем какую-нибудь точку. Пусть х = 1, тогда у= -1. Получим точку Мо (1,-1).
Приведем уравнение второй прямой к нормированному виду:
2x-y+5=0,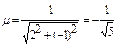 
,
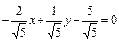
- нормированное уравнение. Тогда по формуле (12) получим
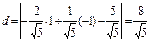(лин.ед.)
Плоскость
Уравнение плоскости с нормальным вектором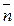 
= {А,В,С} и проходящей через точку M0(x0,y0,zo) имеет вид
А(х -х0) + В(у - у0) + C(z - z0) = 0. (13)
Из этого уравнения получается общее уравнение плоскости
Ax + By + Cz+D=0, (14)
представляющее собой уравнение первой степени относительно переменных x,y и z.
Геометрически удобное уравнение в отрезках
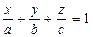, (15)
где а,b,с - величины отрезков, отсекаемых плоскостью на осях координат соответственно.
Нормированное уравнение плоскости
xcosα + ycosβ + zcosg-ρ = 0, (16)
где ρ - расстояние плоскости от начала координат; a,β,g - углы образованные единичным вектором нормали к плоскости (он направлен от начала координат к плоскости) с соответствующими осями координат. Если дана плоскость общим уравнением (14), то
μ Ах + μ Dy + μ Сz + μ D = О
будет нормированным уравнением той же плоскости, если
,
где знак выбирается противоположным знаку D - свободного члена в общем уравнении.
Нормированное уравнение (16) позволяет получить отклонение δ и
расстояние d от заданной точки Мо (х0, у0,z0) до плоскости
δ = x0cosα + y0cosβ + z0cosγ -ρ, (17)
d = \ δ \. (18)
Условия перпендикулярности, параллельности и угол между плоскостями совпадают с аналогичными условиями для векторов, нормальных к этим плоскостям.
Прямая в пространстве
Прямая в пространстве может быть задана как линия пересечения двух плоскостей
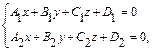(19)
причем должно нарушаться хотя бы одно из равенств
,
чтобы эти плоскости пересекались.
Другой способ задания прямой:
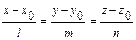(20)
каноническими уравнениями, где М0(x0, у0,z0) - точка, через которую проходит прямая в направлении вектора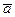 
= {1,т,п}. Тогда условия параллельности, перпендикулярности и угол между прямыми могут быть получены как соответствующие условия для направляющих векторов этих прямых.
Из (20) могут быть получены уравнения прямой, проходящей через две точки М1{x1, y1, z1) и M2(x2,y2,z2)
(21)
и параметрические уравнения прямой:
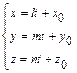. (22)
Если прямая задана уравнениями (19), то можно получить канонические уравнения этой прямой, если взять какую-нибудь точку, задавая, например, х0 и отыскивая соответствующие у0 и z0 из системы (19), и получить направляющий вектор прямой
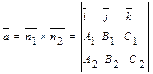
Если прямая задана уравнениями (20), а плоскость общим уравнением (14), то условие параллельности прямой и плоскости
Аl + Вт+Сп = 0, (23)
а условие перпендикулярности
.
Пример 4. Привести уравнение прямой
к каноническому виду.
Решение. Найдем какую-нибудь точку на этой прямой. Пусть х = 0, тогда система примет вид
.
Отсюда y=-2,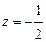 
. Получим точку Мо (0;- 2; 
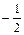)Найдем направляющий вектор
Канонические уравнения прямой
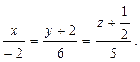
Пример 5. Составить уравнения движения точки M(x,y,z), которая имеет начальное положение Мо(1;-2;4), движется прямолинейно и равномерно в направлении вектора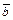 
= {2; 3; 6} со скоростью 
, 
.
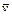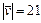Решение.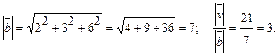 
Тогда 
. Искомые уравнения будут
Пример 6. Найти расстояние точки М0(1;2;0) от прямой
Решение. Проведем через точку Мо плоскость α, перпендикулярную данной прямой и найдем М1 - точку пересечения плоскости α с данной прямой. Тогда искомое расстояние будет расстоянием от Мо до М1. Для плоскости α воспользуемся уравнением вида (13), так как известна точка М0(1;2;0) на ней лежащая и нормальным вектором может служитьнаправляющий вектор прямой а= {2,5,1}. Получим
2(х -1) + 5(у - 2) + 1(z- 0) = 0,
или
2x + 5y + z-12 = 0.
Найдем точку пересечения плоскости α и данной прямой, решив систему из уравнений плоскости α и параметрических уравнений данной прямой:
Исключая x,y,z, найдем t=-0,5. Тогда х=1,y=1,5,z=2,5. Точка М1(1;1,5;2,5). Расстояние М0М1:
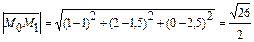(лин.ед.).
Пример 7. Найти угол между прямой
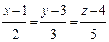
и плоскостью
х + 2у - 3z - 1 = 0.
Решение. Рассмотрим нормальный вектор плоскости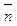 
= {1;2;-3} и направляющий вектор прямой 
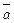= {2;3;5}. Косинус угла между этими векторами равен синусу угла между прямой и плоскостью:
,
.
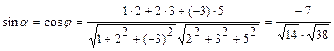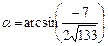Кривые второго порядка
Канонические уравнения:
эллипса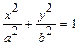 
,
гиперболы 
,
параболы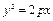 
; 
Эксцентриситеты
эллипса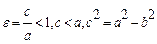 
,
гиперболы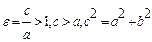 
параболы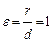 
,
где r и d - расстояния любой точки параболы до фокуса и директрисы соответственно. Уравнение директрисы параболы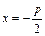 
; 
.
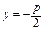Построение кривойв полярной системе координат
Полярная система координат задается точкой О (полюсом), выходящим из нее лучом и единицей масштаба. Полярные координаты точки М - два числа ρ и φ, первое из которых ρ (полярный радиус) равно расстоянию точки М от полюса О, а второе φ (полярный угол) - угол, на который нужно повернуть полярный луч против часовой стрелки до совмещения с лучом ОМ.
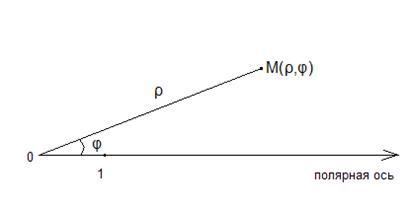
Обычно считают, что ρ и φ изменяются в пределах
,
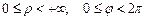чтобы соответствие между точками плоскости и полярными координатами было однозначным.
Замечание. В задачах, связанных с перемещением точки по плоскости (в механике), удобнее отказаться от этих ограничений, когда естественно считать, что при вращении точки угол может быть и больше 2π, а при движении точки по прямой, проходящей через полюс, считать, что при переходе через полюс полярный радиус точки меняет знак на отрицательный.
Пример. Построить график функции ρ = 2 + 3cos φ.
Построение выполняем поточечное. Выяснив область определения функции (
), задаемся для начала значениями φ в интервале [0,2π] и вычисляем соответствующие значения ρ:
| Номер точки | ||||||||||
| j |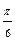 
| 
| 
| 
| 
| 
| 
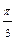
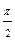
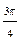
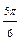
| π |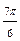 
| |
| r | 4,6 | 4,1 | 3,5 | 0,5 | -0,1 | -0,5 | -1 | -0,5 |
| Номер точки | |||||||
| j |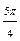 
| 
| 
| 
| 
| 
| 
|
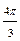
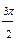
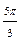
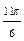
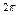
| r | -0,1 | 0,5 | -3,5 | 4,1 | 4,6 |
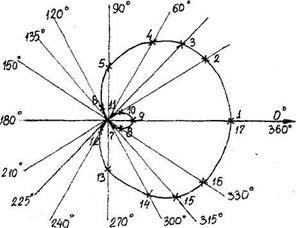Выполним построение с помощью транспортира.
Улитка Паскаля
При значениях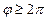 
полученные точки повторяются.
Замечание 1. Если форма кривой неясна, берем промежуточные точки.
Замечание 2. Наиболее часто встречающиеся кривые и их название приведены в справочнике [3].
