Полный математический анализ ферментативной реакции приводит к сложным уравнениям, не пригодным для практического применения. Наиболее удобной оказалась простая модель, разработанная в 1913 г Михаэлисом и его сотрудницей Ментен. Она объясняет характерную гиперболическую зависимость скорости реакции при постоянной концентрации фермента от концентрации субстрата и позволяет получать константы, которые количественно характеризуют эффективность фермента.
Модель Михаэлиса-Ментен исходит из того, что вначале субстрат (S) обратимо образует с ферментом (E) комплекс (ЕS), который,быстро превращается в продукт Р, что можно выразить следующей схемой:
Математическая обработка этой системы уравнений с использованием закона действующих масс и уравнения материального баланса позволяет вывести уравнение, названное в честь авторов уравнением Михаэлиса–Ментен, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:
Вывод уравнения Михаэлиса-Ментен:
Скорость прямой реакции образования ES - Vпр = K+1[E][S] 1
Скорость обратной реакции - Vобр = К-1[ES] 2
В стационарном состоянии, т.е. когда концентрация ES постоянна скорость прямого процесса равна скорости обратного - Vпр = Vобр или K+1[E][S] = К-1[ES]
Отсюда имеем: [E][S]/[ES] = K-1/K+1 = Кs 3
[E][S]/[ES] = K-1/K+1 = Кs – константа диссоциации фермент-субстратного комплекса
Из уравнения материального баланса имеем: аналитическая концентрация фермента ([Eобщее]) равна сумме концентраций свободного фермента ([E]) и фермент-субстратного комплекса ([ES]): - [Eобщее] = [E] + [ES] 4
Скорость образования продукта реакции Р равна - Vобр продукта = К+2 [ES] 5
Из уравнения (3) имеем: [ES] = [E][S]/Ks, а из уравнения (4) - [E] = [Eобщ ] – [ES], после
подстановки этого значения в предыдущее уравнение получаем:
[ES] = ([Eобщ ] – [ES])∙[S]/Ks 6
После преобразования уравнения (6) относительно [ES] имеем:
[ES] = [Eобщ][S]/(Ks + [S]) 7
Подставляя уравнение (7) в уравнение (5) получаем:
Vобр продукта = K+2 [Eобщ][S]/Ks + [S] 8
Очевидно, что скорость реакции образования продукта будет максимальной при данных условиях когда [ES] = [Eобщ ], т.е. - K+2 [Eобщ] = Vmax
Вводя это значение в уравнение (8) получаем уравнение в виде:
которое называется уравнением Михаэлиса-Ментен, где:
· v – наблюдаемая скорость реакции при данной концентрации субстрата [S];
· KS– константа диссоциации фермент-субстратного комплекса, моль/л;
· Vmax– максимальная скорость реакции при полном насыщении фермента субстратом.
KS и Vmax – это константы, которые не зависят от концентрации субстрата, а характеризуют свойства фермента.
Теоретический график зависимости скорости ферментативной реакции (V) от концентрации субстрата [S] при постоянной концентрации фермента представляет собой график гиперболы.
Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении KS скорость реакции является максимальной, (реакция нулевого порядка – участок (в) на графике). При низкой концентрации субстрата, напротив, скорость реакции оказывается пропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка v = Vmax∙[S] – участок (а) на графике). При средних значениях концентрации субстрата скорость реакции имеет смешанный порядок (участок (Б) на графике) и описывается уравнением Михаэлиса-Ментен.
Следует отметить, что уравнение Михаэлиса–Ментен в его классическом виде было выведено с использованием ряда допущений и, в частности, что образование продукта реакции идет быстро и необратимо. В реальной ферментативной кинетике как раз, как правило, образование продукта реакции процесс обратимый, т.е. более реальная схема ферментативного процесса должна учитывать как минимум 4 константы:
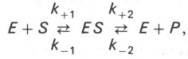
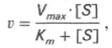Поэтому были предприняты попытки усовершенствовать уравнение Михаэлиса-Ментен. В том же 1913 году несколько позднее была опубликована работа Бриггса и Холдейна, в которой было предложено уравнение, выведенное в результате анализа рассматриваемой схемы. Однако это уравнение Бриггса-Холдейна:
по сути мало отличается от уравнения Михаэлиса-Ментен. Отличие заключается в том, что вместо константы диссоциации фермент-субстратного комплекса Кs = K-1/K+1 в уравнении используется более сложная константа названная позднее константой Михаэлиса Кm. Константа Михаэлиса (Кm) может быть представлена следующим уравнением:
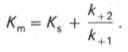
Ферментативная активность. Каталитическая константа - число оборотов фермента. Максимальная скорость ферментативной реакции (Vmax). Константа диссоциации фермент-субстратного комплекса (Ks). Константа Михаэлиса-Ментен (Km).
Особенностью ферментативной кинетики является также то, что экспериментально измеряется не скорость ферментативной реакции, а активность фермента (ферментативная активность). Ранее в лекции №2 уже давалось определение ферментативной активности
Поскольку ферментативная активность не зависит от объема раствора, в котором протекает реакция (она пропорциональна концентрации фермента) ее выражают в специальных единицах: Если размерность скорости реакции – моль/ л·с, то размерность ферментативной активности моль субстрата, превращаемого в единицу времени. Используются следующие единицы активности ферментов:
- Катал. 1 кат = количеству фермента, которое превращает 1 моль субстрата за 1 сек.
- Нкат – нонакатал; 1нкат = 109кат
- Международная единица ферментативой активности (Е) – количество фермента, превращающего 1 мкмоль субстрата в 1 мин.
1Е = 16,7 нкат.
Удельная активность выражается либо 1) количеством единиц (Е или кат, нкат) на 1 мг белка, либо 2) числом молей продукта образовавшегося за 1 минуту на 1 мг белка. Суммарная ферментативная активность определяется как произведение удельной активности на общее количество фермента.
Рассмотрим физический смысл констант уравнения Михаэлиса-Ментен: каталитической константы (К2), максимальной скорости ферментативной реакции (Vmax), константы диссоциации фермент-субстратного комплекса (Ks) и константы Михаэлиса-Ментен (Km).
1. Константа скорости k2 намного выше, чем константа той же, но некаталитической реакции. Константу k2называют каталитической константой скорости ферментативной реакции Ее физический смысл заключается в том, что она соответствует числу молекул субстрата, превращаемых в продукт одной молекулой фермента за 1 сек. В связи с этим каталитическая константа еще называется «числом оборотов фермента».
Число оборотов фермента позволяет характеризовать активность ферментов, молекулярная масса которых известна. Чем больше число оборотов фермента, тем он более активен. В настоящее время около 2000 ферментов выделено в чистом виде и молекулярная масса определена у около 150 ферментов. Самым активным ферментом оказалась карбоангидраза, которая катализирует реакцию гидратации углекислого газа. Для нее число оборотов составляет 600.000 сек-1. Амилаза, которая катализирует гидролиз крахмала, имеет число оборотов 18.300 сек-1, число оборотов большей части ферментов определяется трех- или четырехзначным числом. Это свидетельствует о высокой активности ферментов. Если фермент не получен в чистом виде, то его активность определяется количеством молей преобразованного субстрата в одну минуту в расчете на 1 мг белка. Эта величина называется удельной активностью фермента. Очевидно, что чем чище ферментный препарат, тем выше окажется его удельная активность.
2. Максимальная скорость реакции (Vmax) как видно из уравнения равна k+2[Eобщ]. Очевидно, что эта величина является константой для данной реакции, проводимой с данной концентрацией фермента, т.е. эта величина также характеризует активность фермента. Если молекулярная масса фермента известна, то экспериментальное значение максимальной скорости реакции при данной молярной концентрации фермента легко может быть пересчитано в число оборотов.
3. Константа диссоциации фермент-субстратного комплекса (Ks) характеризует устойчивость фермент-субстратного комплекса. Чем меньше значение константы тем стабильнее фермент-субстратный комплекс.
4. Константа Михаэлиса (Кm) характеризуетсродствофермента к субстрату. Высокое сродство фермента к субстрату характеризуется низкой величинойКm и наоборот. Величина Кm всегда численно больше чем величинаKs. Константа Михаэлиса численно равна той концентрации субстрата [S], при которой ν достигает половины максимальной величины Vmax (действительно, если v = Vmax/2, то [S] / (Кm + [S]) = 1/2, отсюда Кm = [S]).
