Практическая работа№1
Тема «Решение систем линейных уравнений»
Цель: сформировать умение исследовать и использовать различные методы для решения систем линейных алгебраических уравнений.
Теоретическая часть:
Метод Крамера.
Метод Крамера применяют при решении систем, в которых число уравнений и количество неизвестных совпадают (m = n).
Рассмотрим систему двух линейных уравнений с двумя неизвестными
 (1)
(1)
Если определитель Δ системы отличен от нуля, то система имеет единственное решение, которое находится по формулам Крамера:
x =  , y =
, y =  , где Δ =
, где Δ =  ,
,  =
=  ,
,  =
=  . (2)
. (2)
Если Δ = 0, а хотя бы один определитель 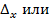
 не равен нулю, то система (1) не имеет решений (несовместна).
не равен нулю, то система (1) не имеет решений (несовместна).
Если Δ =  =
=  = 0, то система имеет бесконечное множество решений (неопределенна).
= 0, то система имеет бесконечное множество решений (неопределенна).
Теперь рассмотрим систему трех линейных уравнений с тремя неизвестными
 (3)
(3)
Системе (2) соответствует определитель, составленный из коэффициентов при неизвестных x,y и z.
Δ =  - определитель системы. По аналогии с (2) составим еще три определителя:
- определитель системы. По аналогии с (2) составим еще три определителя:
 ,
,  ,
,  = =
= =  , (4)
, (4)
каждый из которых получен из определителя системы заменой столбца коэффициентов при соответствующей неизвестной столбцом свободных членов системы.
Правило Крамера. Если определитель системы (3) отличен от нуля, то система имеет единственное решение:
 =
=  , y =
, y =  , z =
, z =  (5)
(5)
Если же определитель системы  а хотя бы один из определителей
а хотя бы один из определителей 
 отличен от нуля, то система (3) не имеет решений, т. е несовместна.
отличен от нуля, то система (3) не имеет решений, т. е несовместна.
Если Δ =  =
=  =
=  = 0, то система имеет бесконечное множество решений (неопределенна)
= 0, то система имеет бесконечное множество решений (неопределенна)
Образец выполнения задания:
Пример 1. Решить систему уравнений методом Крамера.

Для этого нам потребуется вычислить четыре определителя:  и
и 

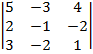 = 5
= 5  – (
– ( 3)
3)  + 4
+ 4  = 5∙(
= 5∙( 5) + 3∙(
5) + 3∙( ) + 4∙ (
) + 4∙ ( 1) =
1) =  25
25 
 4=
4=  5. Определитель не равен нулю, следовательно, система имеет единственное решение.
5. Определитель не равен нулю, следовательно, система имеет единственное решение.
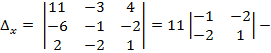 (
( 3)
3)  + 4
+ 4  =
=
= 11 ∙ ( 5) + 3
5) + 3  + 4
+ 4  =
=  ;
;
 = 5
= 5 
 + 4
+ 4  =
=
= 5 ∙ (
 = 5
= 5 
 + 11
+ 11  =
=
= 5  (
( + 3
+ 3 
Тогда по формулам (5) получаем:
 =
=  ; y =
; y =  = 2; z =
= 2; z = 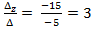 .
.
Ответ: (1;2;3).
Пример 2.
. 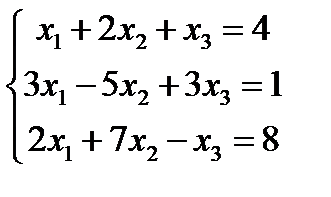
Составляем главный определитель, элементами которого являются коэффициенты при неизвестных:

и три вспомогательных определителя:
 ;
;  ;
;  .
.
Определитель  составлен из определителя
составлен из определителя  путем замены элементов первого столбца свободными членами системы уравнений. В определителях
путем замены элементов первого столбца свободными членами системы уравнений. В определителях  и
и  соответственно второй и третий столбцы заменены свободными членами. Вычислим все четыре определителя.
соответственно второй и третий столбцы заменены свободными членами. Вычислим все четыре определителя.
 ;
;
 ;
;
 ;
;
 .
.
Неизвестные  ,
,  ,
,  находим по формулам
находим по формулам
 ;
;  ;
;  ;
;
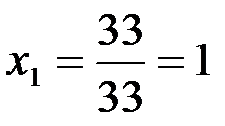 ;
;  ;
;  .
.
Ответ:  ;
;  ;
;  .
.
Пример3. Решить систему  методом Крамера.
методом Крамера.
Решение. Выписываем A - матрицу системы и B - столбец свободных членов:  ,
,  . Далее вычисляем определители:
. Далее вычисляем определители:
 ;
;
 ;
;
 ;
;
 .
.
По теореме Крамера 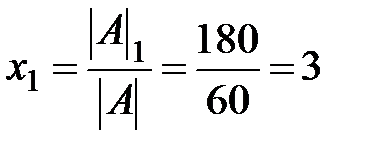 ;
;  ;
;  .
.
Ответ:  ;
;  ;
;  .
.
Для проверки результата подставим полученные значения неизвестных в каждое уравнение системы:  ,
,  ,
,  . Все уравнения обратились в тождества, значит, решение найдено верно.
. Все уравнения обратились в тождества, значит, решение найдено верно.
Метод Гаусса решения систем линейных уравнений.
Сведения из теории:
Метод Гаусса представляет собой специальный
алгоритм последовательного исключения неизвестных из уравнений
системы. В этом алгоритме обычно различают два этапа:
Первый этап называется прямой ход,
Второй этап – обратный ход.
Цель прямого хода метода Гаусса заключается в приведение матрицы системы к треугольному виду, когда в результате некоторых элементарных преобразований уравнений системы на главной диагонали матрицы системы будут располагаться ненулевые элементы, а все элементы ниже главной диагонали будут равны нулю. В результате наших преобразований должна получаться система, равносильная исходной системе линейных уравнений. Преобразования, которые позволяют свести исходную систему к треугольной, сохраняя равносильность, называются элементарными. Что будем понимать под элементарными преобразованиями? Или, говоря простым языком, что можно делать с уравнениями, входящими в систему, чтобы сохранить множество решений системы и не получить лишних корней?
Определение. Элементарными преобразованиями уравнений
системы называют следующие преобразования:
1) перестановка местами двух любых уравнений;
2) умножение обеих частей какого-либо уравнения на любое число, не равное нулю;
3) прибавление к обеим частям одного из уравнений соответствующих частей любого другого уравнения;
4) перестановка (перенумерация) неизвестных системы.
Примем без доказательства, что все перечисленные преобразования
приводят к системам, которые равносильны (эквивалентны) исходной системе линейных уравнений.
Удобно в методе Гаусса работать не с самой системой линейных уравнений, а с основой системы – расширенной матрицей. Эту матрицу обозначают символом
Ā= (A | B), и она содержит две части – матрицу A системы и столбец B свободных членов.
Элементарным преобразованиям системы соответствуют следующие элементарные преобразования расширенной матрицы:
1) умножение произвольной строки на любое число, отличное от нуля;
2) прибавление к произвольной строке матрицы любой другой строки матрицы;
3) перестановка местами любых двух строк;
4) перестановка местами любых двух столбцов матрицы A системы.
Образец выполнения
Пример 1. Решить систему уравнений:

.Расширенная матрица системы будет иметь вид:
Ā= (A | B) = 
Выполним прямой ход метода Гаусса.
Процесс приведения матрицы системы к треугольному виду состоит из нескольких шагов:
Первый шаг.
Надо элемент  сделать равным единице. Так как мы имеем право переставлять строки, умножать на число какую-либо строку и складывать ее с любой другой строкой, то вычтем из второй строки первую и поставим результат на место первой строки, соответственно первая строка станет второй, а третья останется на своем месте. Получим:
сделать равным единице. Так как мы имеем право переставлять строки, умножать на число какую-либо строку и складывать ее с любой другой строкой, то вычтем из второй строки первую и поставим результат на место первой строки, соответственно первая строка станет второй, а третья останется на своем месте. Получим:
Ā~ 
Важно то, что между двумя матрицами нет знака равенства, – его заменяет следующий символ ~ эквивалентности двух систем (матрицы разные, а соответствующие им системы уравнений имеют одинаковые решения).
Второй шаг.
Необходимо сделать, чтобы равнялись нулю все элементы 1-го столбца, матрицы A, расположенные ниже элемента  .
.
Для этого надо ко второй строке прибавить первую строку, умноженную на (-2). Аналогично, прибавить к третьей строке первую, умноженную на (-4).
Получим: Ā~ 
Третий шаг.
На третьем шаге получим нулевой элемент во втором столбце ниже элемента 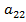 .
.
Для этого вторую строку последней матрицы умножим на (-7), а третью строку на 5 и прибавим вторую
строку к третьей:
Ā~  (*)
(*)
Прямой ход выполнен, в результате мы получили треугольную матрицу (*)
Теперь выполним обратный ход, для чего перейдем от матричной записи к соответствующей системе уравнений:

Из названия хода (обратный), понятно, что надо начинать с последнего уравнения, т.к. в нем содержится одна неизвестная z. Находим:
z = -2, теперь подставим значение z во второе уравнение, получим:
y =  = 1,
= 1,
Далее подставим значения y = 1 в первое уравнение:
x = 2y = 2 
Система имеет единственное решение (2;1;-2).
Ответ: (2;1;-2).
Метод Гаусса – творческий метод. В этом его большое преимущество перед другими методами, т.к. указанное решение не является единственно возможным. И чем гибче мыслит человек, тем короче получается у него решение.
Пример 2. Решить систему уравнений:

Ā = 
Получили несовместную систему, так как из последней строки расширенной матрицы получаем уравнение:
0  x + 0
x + 0  + 0
+ 0  , которое не имеет решения.
, которое не имеет решения.
Матричный метод
Систему можно решить и матричным способом.
Рассмотрим систему вида

(4)
Составим матрицу системы из коэффициентов при неизвестных:
 .
.
Из неизвестных  ,
,  ,
,  и свободных членов составим матрицы – столбцы
и свободных членов составим матрицы – столбцы
 ;
;  .
.
Тогда система (4) в матричной форме примет вид
 . (5)
. (5)
Чтобы найти матрицу  , умножим (7) на
, умножим (7) на  слева.
слева.
A 

Пример 4.
 .
. 
Найти обратную матрицу  .
.
РЕШЕНИЕ.
1) Составляем и вычисляем определитель
 .
.
Определитель вычислен по правилу треугольника.
2) Транспонируем матрицу. Получаем
 .
.
3) Вычисляем алгебраические дополнения
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
 ;
; 
Вычисляем  . Вычеркиваем первую строку и второй столбец. Составляем определитель второго порядка из оставшихся элементов.
. Вычеркиваем первую строку и второй столбец. Составляем определитель второго порядка из оставшихся элементов.
 ;
;  .
.
Вычисляем  .
.
Аналогично вычисляем все остальные алгебраические дополнения:
 ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 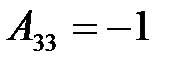 .
.
Составим обратную матрицу
A 
A 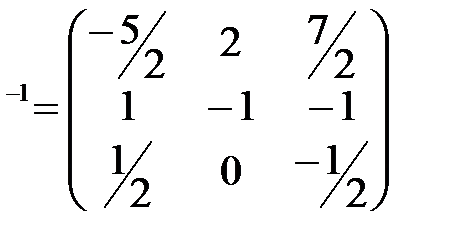
Сделаем проверку

Пример 2.
Решить систему матричным способом
 .
.
Из коэффициентов при неизвестных составим матрицу  :
:
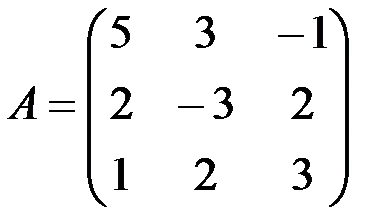 .
.
Из неизвестных составим матрицу – столбец:
 .
.
Из свободных членов составим матрицу – столбец:
 .
.
Тогда система запишется в виде
 .
.
Получили матричное уравнение. Умножаем обе части этого уравнения на 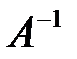 слева. Получаем:
слева. Получаем:
 .
.
Находим обратную матрицу:
 ;
;  ;
;
 (матрица, составленная из алгебраических дополнений элементов;
(матрица, составленная из алгебраических дополнений элементов;  (обратная матрица).
(обратная матрица).
Умножая обратную матрицу на  , получаем матрицу
, получаем матрицу  .
.
 .
.
Отсюда получаем ответ:
 ;
;  ;
;  .
.
ЛИТЕРАТУРА
1. Дадаян А.А. Математика М.: ФОРУМ – ИНФРА-М,2011.552 с.
2. Высшая математика в упражнениях и задачах. В 2ч.: учеб. пособие / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 7-е изд., испр. – М.: Оникс: Мир и образование, 2009.
3. Богомолов Н.В. Практические занятия по математике: Учеб. пособие для средних спец. учеб. заведений – 6-е изд. стер.- М.: Высш. шк., 2003. – 495 с.
4. Апанасов П.Т. Орлов М.И. Сборник задач по математике: Учеб. пособие для техникумов – М: Высш. шк., 1987.- 303 с.






