Деление окружности на равные части

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

Контуры изображаемых деталей образуют прямые линии, коробовые и лекальные кривые. При вычерчивании изображений применяют следующие построения:

– деление отрезков и углов;

– деление окружности на равные части;

– сопряжение линий;

– построение уклона и конусности.

Деление отрезка на части

Отрезок прямой линии можно поделить пополам и на равные или пропорциональные части.

Деление отрезка пополам выполняют следующим образом (рисунок 2.2а):

– из точек A и B радиусом R > 0,5AB проводят дуги до пересечения в точках C и D;

– через точки C и D проводят прямую линию, которая делит отрезок пополам (точка E).

Деление отрезка на несколько равных частей выполняют следующим образом (рисунок 2.2б):

– из точки A отрезка AB под произвольным углом проводят прямую линию и делят ее на заданное число равных отрезков (точки 1, 2, 3, C);

– точку C соединяют с точкой B;

– из точек 1, 2, и 3 параллельно отрезку BC, проводят прямые линии, до пересечения с отрезком AB в точках 1', 2' и 3'.

Деление отрезка на пропорциональные части, например, в соотношении 1:2 выполняют в следующей последовательности (рисунок 2.2в):

– из точки A отрезка AB под произвольным углом проводят прямую линию и делят ее на три равные части. Отношение отрезков AD:DC = 1:2;

– точку C соединяют с точкой B;

– из точки D проводят прямую параллельно отрезку BC.

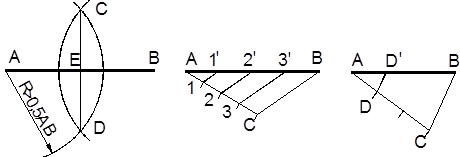
а) б) в)

Рисунок 2.2

Деление угла на две равные части

Деление угла на равные части выполняют в следующей последовательности (рисунок 2.3):

– из вершины угла B произвольным радиусом R проводят дугу до пересечения со сторонами угла в точках D и C;

– из точек D и C произвольным радиусом R₁ проводят дуги до пересечения в точке K;

– соединяют точки B и K (отрезок BK делит угол пополам).

Деление окружности на равные части

Пример деления окружности на равные части приведен на рисунке 2.4.

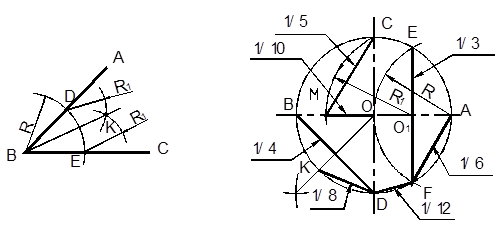
Рисунок 2.3 Рисунок 2.4

Справа от оси CD показано деление окружности на три, шесть и двенадцать частей, для чего:

– из точки A радиусом R окружности проводят дугу до пересечения с окружностью в точках F и E. Отрезок FE отсекает треть окружности, AF – шестую, а DF – двенадцатую часть окружности.

Слева над осью АВ показано деление окружности на пять и десять частей (выше оси AB), для чего:

– из точки A радиусом R окружности проводят дугу до пересечения с окружностью в точках F и E;

– из точки E строят перпендикуляр до пересечения с осью AB (точка O₁);

– из точки O₁ радиусом R₁ = O₁C проводят дугу до пересечения с осью AB (точка М). Отрезок CM делит окружность на пять, а отрезок OM на десять равных частей.

Слева ниже оси AB показано деление окружности на четыре и восемь равных частей, для чего:

– соединяют точки B и D;

– делят отрезок BD пополам (см. пункт 2.3.1);

– из центра О проводят прямую перпендикулярную BD до пересечения с окружностью (точка К). Отрезок BD делит окружность на четыре, а отрезок KD – на восемь равных частей.

Построение треугольника

Пример построения треугольника по трем заданным сторонам приведен на рисунке 2.5.

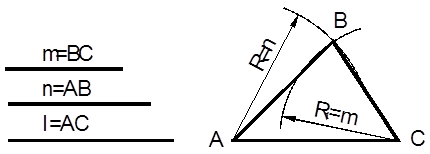
Рисунок 2.5

Из концов стороны АС треугольника радиусами R=n и R₁=m проводят дуги до пересечения в точке В и соединяют точку В с точками А и С.

 

Построение уклона

Уклоном i прямой АС относительно прямой АВ называется тангенс угла между этими прямыми, т.е. i = (h/l) = tga, где h – разность аппликат концов отрезка АС; l – разность абсцисс отрезка АВ (рисунок 2.6).

На рисунке 2.7 показано построение и обозначение различных уклонов.

 

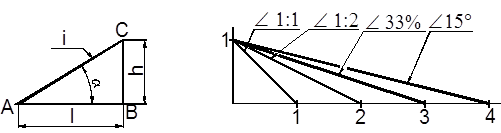
Рисунок 2.6 Рисунок 2.7

Уклон на чертеже указывают с помощью линии-выноски, на полке которой наносят знак и значение уклона (ГОСТ 2.307 - 68).

Уклон обозначается знаком «Ð», а величина его выражается дробью, в процентах и градусах, например, Ð 1:5; Ð 20 %; Ð 15⁰. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть параллельна основанию уклона (АВ), а другая – наклонена под углом 30⁰ к ней, при этом острие знака всегда направлено в сторону уклона.

Построение конусности

Конусность C (рисунок 2.8) определяется отношением разности диаметров двух поперечных сечений конуса к расстоянию между сечениями: C = (D – d)/H = 2tga.

Конусность на чертеже указывают с помощью линии-выноски, на полке которой наносят знак и значение конусности (ГОСТ 2.307 - 68).

Конусность обозначается знаком «>», острие которого направлено в сторону вершины конуса, а величина её выражается дробью или в градусах, например, > 1:5; >30⁰. На рисунке 2.9 показано построение и обозначение конусности.

 

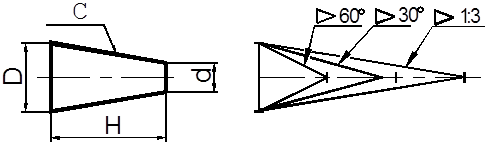
Рисунок 2.8 Рисунок 2.9

Построение усеченного конуса с заданным диаметром большего основания D, высотой H и конусностью равной 1:4 (рисунок 2.10) выполняется в следующей последовательности:

– откладываем высоту конуса H=ОО₁ на оси симметрии;

– через точку O проводим перпендикуляр, на котором симметрично от оси откладываем диаметр большого основания D=ОC+ОB=BC;

– из точки O по оси

Рисунок 2.10 OO₁откладываем четыре равных отрезка произвольной длины OA=4a;

– от точки O симметрично от оси откладываем отрезок a=OE+OF=FE;

– соединив точки F и E с точкой A, получим вспомогательный конус с конусностью 1:4;

– через точки B и C проводим прямые линии параллельные образующим вспомогательного конуса до пересечения с перпендикуляром, проведенным через точку O₁. Полученные точки K и L ограничивают величину малого основания усеченного конуса.

СОПРЯЖЕНИЕ ЛИНИЙ

Очертание многих деталей и узлов состоит из линий, плавно переходящих одна в другую, называемых сопряжением. Из многообразия сопряжений линий можно выделить следующие:

– сопряжение двух прямых линий дугой окружности;

– сопряжение прямой линии с дугой окружности при помощи другой дуги окружности;

– сопряжение двух дуг окружности при помощи третьей дуги.

Сопряжение двух сторон угла дугой окружности (рисунок 2.11) выполняется следующим образом:

– параллельно сторонам угла AB и BC на расстоянии равном радиусу дуги R проводят прямые линии n и m до пересечения в точке О;

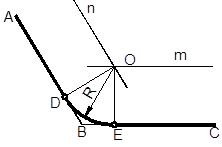– из точки O опускают перпендикуляры на сопрягаемые стороны. Точки D и E являются точками сопряжения;

– из точки O радиусом R = OD проводят дугу плавно переходящую в прямые линии.

При выполнении сопряжения прямой линии с дугой окружности возможны два случая сопряжения:

Рисунок 2.11 внешнее и внутреннее.

Внешнее сопряжение прямой линии с дугой окружности (рисунок 2.12а) выполняется следующим образом:

– из центра О строят дугу радиусом R₂= R+R₁, где R₁ – радиус сопряжения;

– на расстоянии R₁ от заданной прямой n проводят параллельную прямую m;

– определяют центр О₁ сопряжения как результат пересечения дуги окружности радиусом R₂= R+R1 с прямой m;

– из точки O₁ опускают перпендикуляры на сопрягаемые прямую m и дугу (точки сопряжения A и B);

– из центра О₁ строят дугу AB сопряжения радиусом R₁.

Внутреннее сопряжение прямой с дугой окружности (рисунок 2.12б) выполняется так:

– из заданного центра заданной дуги окружности строят дугу радиусом R₂ = R-R₁, где R₁ – радиус сопряжения;

– на расстоянии R₁ от заданной прямой n проводят прямую m параллельно n до пересечения в точке О₁ (центр сопряжения);

– определяют точки сопряжения, для чего из полученного центра О₁ опускают перпендикуляр на прямую n, а через точки О и О₁ проводят линию до пересечения с заданной дугой (точки сопряжения А и В);

– из полученного центра О₁ проводят дугу AB сопряжения радиусом R₁.

При выполнении сопряжения двух дуг окружности третьей дугой различают внешнее, внутреннее и смешанное сопряжение. Во всех трех случаях необходимо определить положение центра дуги сопряжения О₂ и точек сопряжения A и B.

а) б)

Рисунок 2.12

Внешнее сопряжение (рисунок 2.13а) выполняется следующим образом:

– из центров дуг окружностей О и О₁ радиусами R₃=R+R₂ и R₄=R₁+R₂, соответственно, проводим дуги до их пересечения в точке О₂;

– соединяем центр сопряжения О₂ с центрами дуг окружностей О и О₁ прямыми линиями О₂О и О₂ О₁ до пересечения с дугами окружностей в точках А и В (точки сопряжения);

– из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

Пример выполнения внутреннего сопряжения приведен на рисунке 2.13б:

– из центров дуг окружностей О и О₁ радиусами R₃=R₂–R и R₄=R₂–R₁ проводим дуги до их пересечения в точке О₂;

– соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁ (точки сопряжения А и В);

– из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

Выполнение смешанного сопряжения приведено на рисунке 2.13в:

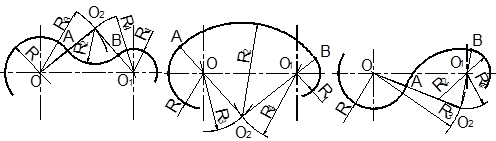
а) б) в)

Рисунок 2.13

– из центров дуг окружностей О и О₁ радиусами R₃=R+R₂ и R₄=R–R₂, соответственно, проводим дуги до их пересечения в точке О₂;

– соединяем центр сопряжения О₂ с центрами дуг окружностей прямыми линиями О₂О и О₂ О₁;

– из центра сопряжения О₂ радиусом R₂ проводим дугу между точками сопряжения A и B.

Построение кривых линий

Различают коробовые и лекальные кривые линии. Данные для построения кривых линий выбирают по таблице 2.2.

Коробовая линия – выпуклая кривая замкнутая линия, состоящая из сопряженных дуг окружностей различных радиусов. Наиболее распространенными из них являются овалы.

Лекальные линии – кривые линии, построение которых выполняется по предварительно определенным точкам с помощью лекал. Лекальными кривыми являются, например, эллипс, парабола, гипербола.

Построение овала

Овал представляет собой сопряжение двух дуг одного радиуса с двумя дугами другого радиуса.

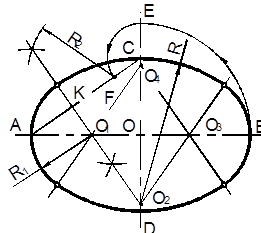Существует несколько способов построения овала. Построение овала по двум осям (рисунок 2.14) выполняется следующим образом:

– проводят осевые линии, на которых симметрично от точки пересечения O откладывают отрезки AB и CD, равные большой и малой осям овала. На малой оси откладывают расстояние OE=OA и сое- Рисунок 2.14 диняют точки A и C;

– на отрезке AC откладывают отрезок CF=CE;

– делят отрезок AF пополам (см. п. 2.2), и через точку K проводят прямую перпендикулярную AF до пересечения с большой и малой осями овала в точках O₁ и O₂;

– строят зеркальное отображение точек O₁ и O₂ (точки O₃ и O₄);

– из точек O₂ и O₄ радиусом R= O₂C, а из точек O₁ и O₃ радиусом R₁=O₁A проводят дуги до их пересечения с прямыми, проведенными через центры дуг (точки сопряжения).

Построение эллипса

Эллипс – замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек, называемых фокусами, лежащих на большой оси является постоянной величиной, равной длине большой оси.

Таблица 2.2 – Исходные данные для построения кривых линий

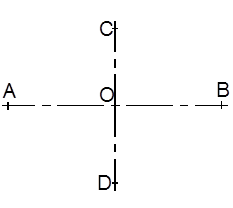AB=a; CD=b   Овал	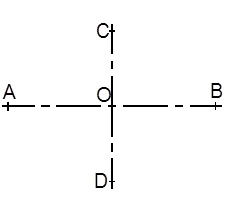AB=a; CD=b   Эллипс
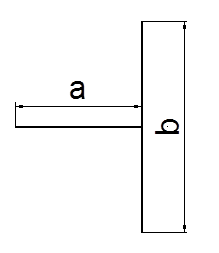Парабола	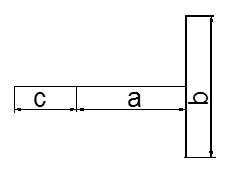Гипербола

 

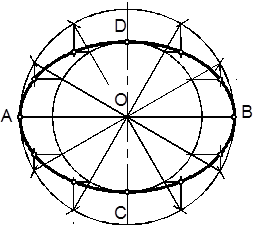Существует несколько способов построения эллипса. Один из способов – построение эллипса по двум осям (рисунок 2.15) выполняется следующим образом:

– проводят осевые линии, на которых симметрично от точки пересечения O откладывают отрезки AB и CD, равные большой и малой осям эллипса;

– строят две окружности радиусами равными половине осей эллипса с центром в точке пересечения осей;

– делят окружность на

Рисунок 2.15 двенадцать равных частей. Деление окружности выполняют, как показано в п.2.3.3;

– через полученные точки проводят лучи-диаметры;

– из точек пересечения лучей с соответствующими окружностями проводят прямые линии параллельно осям эллипса до их взаимного пересечения;

– полученные точки соединяют плавной кривой линией при помощи лекал. При построении лекальной кривой линии необходимо выбирать и располагать лекало так, чтобы соединялось как минимум четыре-пять точек.

Построение параболы

Парабола – плоская кривая линия, каждая точка которой равноудалена от прямой перпендикулярной к оси симметрии параболы (директрисы) и от точки F, называемой фокусом, расположенной на оси симметрии. Расстояние KF между директрисой и фокусом называется параметром p параболы.

На рисунке 2.16 показан пример вычерчивания параболы по вершине O, оси OK и хорде CD. Последовательность построения:

– проводят горизонтальную прямую линию, на которой отмечают вершину O и откладывают ось OK;

– через точку K проводят перпендикуляр, на котором симметрично вверх и вниз откладывают длину хорды параболы DC;

– строят прямоугольник ABCD, в котором одна сторона равна оси, а другая – хорде параболы;

– делят на несколько равных частей сторону BC и отрезок KC настолько же равных частей;

– из вершины параболы O проводят лучи через точки 1, 2…С, а через точки 1₁, 2₁…С проводят прямые параллельные оси;

– определяют точки принадлежащие параболе. Например, при пересечении луча О2 с параллельной прямой 2₁ получаем точку принадлежащую параболе;

– полученные точки соединяют плавной кривой линией под лекало. Вторая ветвь параболы строится аналогично.

Существуют и другие способы построения параболы.

Построение гиперболы

Гиперболой называется плоская кривая линия, состоящая из двух разомкнутых симметрично расположенных ветвей, в которых разность расстояний от каждой точки до фокусов F и F₁ является величиной постоянной и равной расстоянию между вершинами гиперболы A и B.

На рисунке 2.17 приведен пример построения гиперболы по заданному расстоянию c между вершинами A и B, хорде b гиперболы и отстоянию a хорды от вершины.

 

 

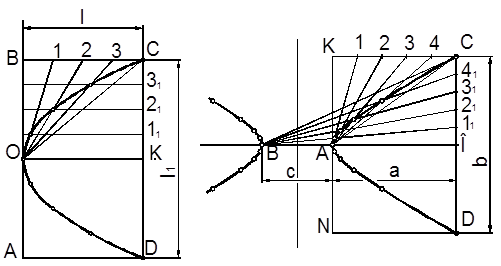
Рисунок 2.16 Рисунок 2.17

 

Построение выполняют следующим образом:

– проводят горизонтальную прямую линию, на которой откладывают расстояние с между вершинами – точки A и B;

– от точки А откладывают отстояние a хордыот вершины гиперболы (точка О), от которой вверх и вниз симметрично откладывают длину хорды b (отрезки ОC и ОD);

– строят прямоугольник KNCD. Сторону прямоугольника KC делят на пять равных частей, а OC на такое же число равных частей;

 

 

– соединяют вершину A с точками 1, 2, …, C, а вершину B с точками 1¹, 2¹,…, C.;

– определяют точки пересечения луча А1 с лучом А1¹, луча А2 с лучом А2¹ и т. д.;

– полученные точки пересечения соединяют плавной кривой линией под лекало.

Остальные ветви гиперболы строят как зеркальное отображение построенной ветви.

 

ПОСТРОЕНИЕ ПРОФИЛЕЙ

Данные для построения профилей выбирают по таблице 2.3 и 2.4.

Построение швеллера

Порядок построения швеллера приведен на рисунке 2.18:

– вычерчивают в тонких линиях стенки и наружные линии полок швеллера (рисунок 2.18а);

– на расстоянии (b – s)/2 откладывают толщину полки t (точки A и B);

– на свободном поле чертежа строят уклон 1:10 (прямые m и n) согласно пункту 2.6;

– через точку A проводят прямую k || m, а через точку B – прямую l || n (рисунок 2.18б);

 

 

а) б) в) г)

Рисунок 2.18

 

 

Таблица 2.3 – Исходные данные для профилей и крюков

Швеллер	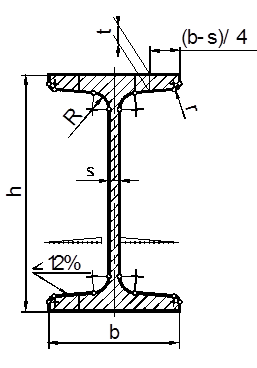Двутавр
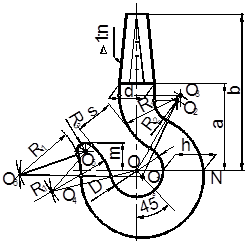Крюк 1	Крюк 2

 

Таблица 2.4 – Параметры профилей и кривых линий в мм

№ варианта	Наименование изображения
Швеллер, двутавр	Коробовые и лекальные кривые
№ про- филя	h	b	s	t	R	r	a	b	c
				4,5	7,6	3,0	3,5			-
				4,5	7,2	7,0	2,5			-
				4,8	7,8	7,5	3,0
				4,8	7,3	7,5	3,0			-
				4,9	8,1	8,0	4,5			-
				4,9	7,5	8,0	3,0
				5,0	8,4	8,5	3,5			-
				5,0	7,8	8,5	3,5			-
				5,1	8,7	9,0	3,5
				5,1	8,1	9,0	3,5			-
				5,2	9,0	9,5	4,0			-
				5,2	8,4	9,5	4,0
				5,4	9,5	10,0	4,0			-
				5,4	8,7	10,0	4,0			-
				5,6	10,0	10,5	4,0
				5,6	9,5	10,5	4,0			-
				6,0	10,5	11,0	4,5			-
				6,0	9,8	11,0	4,5
				6,5	11,0	12,0	5,0			-
				6,5	10,2	12,0	5,0			-
				7,0	11,7	13,o	5,0
				7,0	11,2	13,0	5,0			-
				7,5	12,6	14,0	6,0			-
				7,5	12,3	14,0	6,0
				8.0	13,5	15,0	6,0			-
				8,3	13,0	15,0	6,0			-
				5,4	9,5	10,0	4,0
				9,0	14,2	16,0	7,0			-
				5,6	10,0	10,5	4,0			-
				10,0	15,2	17,0	7,0

– выполняют сопряжение сторон углов в соответствии с пунктом 2.4 (рисунок 2.18в);

– обводят полученный контур профиля сплошной толстой линией;

– проставляют размеры в соответствии с ГОСТ 2.307 - 68;

– выполняют штриховку контура.

Образец выполненного чертежа швеллера приведен на рисунке 2.18г.

 

Построение двутавра

Построение двутавра выполняется в следующем порядке:

– вычерчивают в тонких линиях стенки и наружные линии полок двутавра и на расстоянии (b-s)/4 откладывают толщину полки t (точки A, B, C и D) (рисунок 2.19а);

– на свободном поле чертежа согласно пункту 2.6 строят уклон 3:25, что соответствует 12%, (прямые m и n);

– через точки A и C проводят прямые параллельно прямой m, а через точки B и D – прямые параллельно прямой n (рисунок 2.19б);

– выполняют сопряжение сторон углов в соответствии с пунктом 2.4 (рисунок 2.19в);

– обводят полученный контур профиля сплошной толстой основной линией;

– проставляют размеры в соответствии с ГОСТ 2.307-68;

– выполняют штриховку контура.

Образец выполненного чертежа двутавра приведен на рисунке 2.19г.

 

 

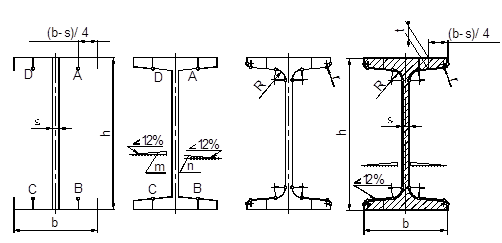
а) б) в) г)

Рисунок 2.19

 

Построение крюка

Данные для построения крюка выбирают из таблиц 2.3 и 2.5.

Таблица 2.5 – Исходные параметры крюка в мм

№ вар.	Наименование изображения
Крюк
а	b	h	m	s	D	d	R1	R2	R3	n

 

 

Построение выполняется в следующем порядке (таблица 2.6):

Таблица 2.6 – Последовательность построения крюка

 

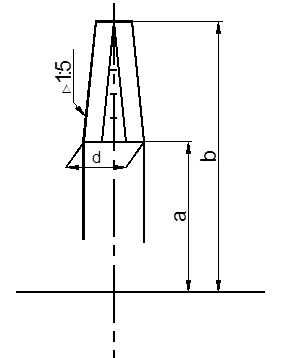
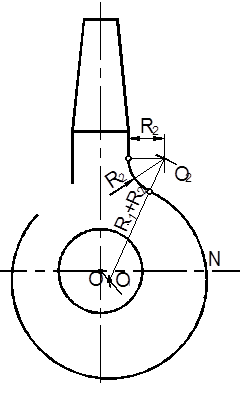
Продолжение таблицы 2.6

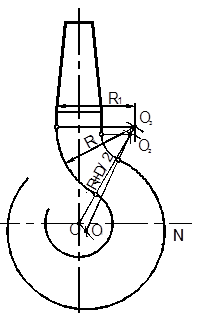
	6.1
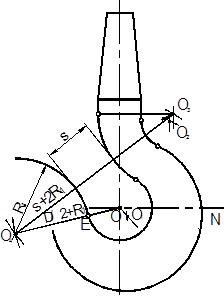
6.2	6.3

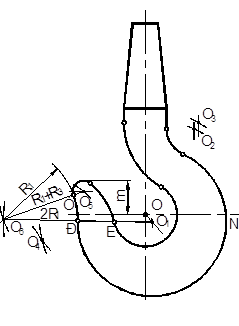
1. Проводим оси и вычерчиваем шейку по размерам, приведенным в таблице 2.5.

2. Проводим из центра О основную окружность внутреннего очертания радиусом R=D/2.

3. Для построения центра окружности внешнего очертания О₁ из центра О проводим прямую п под углом 45⁰ к осям и от точки О на горизонтальной оси делаем засечку радиусом R= D/2+h (точка N). Из точки N радиусом R₁ на прямой п делаем засечку (точка О₁).

4. Строим сопряжение внешней окружности с правым прямолинейным контуром верхней части крюка. Сопрягаемая дуга имеет радиус R₂. Центр сопряжения О₂ и точки сопряжения определяются согласно пункту 2.4.

5. Строим сопряжение внутренней окружности диаметром D с левым прямолинейным контуром верхней части крюка. Сопрягаемая дуга имеет радиус R₁. Центр сопряжения О₃ определяется аналогично центру О₂.

6. Строим очертание носка крюка. Находим центры О₄, О₅, О₆. Носок крюка должен касаться прямой t, которая проведена на расстоянии m от горизонтальной оси крюка. Кроме того зев крюка должен быть равен размеру S. Расстояние S измеряется по линии центров О₃, О₄, ограничивающих контур зева.

6.1. Определяем центр О₄ дуги R₁. Для этого делаем две засечки: первую из центра О₃ радиусом R = 2R₁ + S, вторую из центра O радиусом D/2 + R ₁. Точка сопряжения Е лежит на линии центров O O₄. Из центра О₄ проводим дугу R₁, начиная от точки Е.

6.2. Находим центр О₅ дуги R₃. Для этого сопрягаем прямую, ограничивающую носок сверху, с дугой радиуса R₁ построенную в п. 6.1 На расстоянии R₃ от прямой t проводим прямую e || t. Из О₄ на прямой t делаем засечку дугой R₁ – R₃. Точка сопряжения С лежит на линии центров О₄, О₅. Проводим из центра О₅ дугу радиуса R₃.

6.3. Определяем центр О₆ дуги радиуса R₁, сопрягающей носок крюка с внешним контуром крюка. Для этого делаем две засечки: первую из центра О₅ радиусом R₃ + R₁ и вторую из центра О₁ радиусом R₁ + R₁. Точки сопряжений Т и Р лежат на линиях центров О₆ О₅ и О₆ О₁. Из центра О₆ проводим дугу, соединяющую точки Т и Р.

7. Наносим размеры в соответствии с ГОСТ 2.307 – 68, как показано на рисунке 2.1.

 

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Как выполняется деление отрезка на равные части?

2. Как выполняется деление угла на две части?

3. Как выполняется деление окружности на равные части?

4. Что характеризует величина, называемая уклоном?

5. Что характеризует величина, называемая конусностью?

6. Как выполняется сопряжение двух пересекающихся прямых линий дугой заданного радиуса?

7. Как выполняется сопряжение прямой линии и дуги дугой заданного радиуса?

8. Как выполняется внешнее сопряжение двух дуг дугой заданного радиуса?

9. Как выполняется внутреннее сопряжение двух дуг дугой заданного радиуса?

10. Как выполняется смешанное сопряжение двух дуг дугой заданного радиуса?

11. Какие кривые называются коробовыми?

12. Какая кривая называется эллипсом?

13. Как построить эллипс по двум осям?

14. Какая кривая называется параболой?

15. Какая кривая называется гиперболой?