Принципиальные электрические схемы

Цель работы

Целью работы является определение коэффициента несимметрии токов в питающей сети в схемах с трёхфазным трансформатором, с двумя однофазными и с трансформатором Скотта при различных соотношениях нагрузки на плечах подстанции.

 

Теоретическая часть

Тяговые нагрузки (электровозы) в системе переменного тока промышленной частоты являются однофазными. Они получают питание от понижающих тяговых подстанций. Трансформаторы тяговых подстанций подключены со стороны высокого напряжения к трёхфазной районной сети 110 или 220 кВ, а со стороны низкого напряжения – к однофазной тяговой сети напряжением 25 кВ. Это приводит к неравномерной нагрузке фаз питающих трёхфазных линий, т.е. создаёт в них несимметрию токов и напряжений. Допустимая величина несимметрии часто является существенным фактором при выборе типа и схемы соединения трансформаторов на тяговых подстанциях

На тяговых подстанциях в системе электроснабжения промышленной частоты чаще всего устанавливаются трёхфазные тяговые трансформаторы с первичным напряжением 110 или 220 кВ с тяговой обмоткой 27,5 кВ. Группа соединения обмоток Y/∆-11.

Применяются также и тяговые подстанции с двумя однофазными трансформаторами, соединёнными по схеме открытого треугольника, а также с двумя однофазными трансформаторами, соединёнными по схеме Скотта.

Наилучшими показателями по симметрии токов в питающей сети обладает схема Скотта. При одинаковой нагрузке двух плеч тяговой подстанции она обеспечивает симметричную загрузку питающей сети. Подстанции с трёхфазным трансформатором и с двумя однофазными, соединёнными в открытый треугольник не обеспечивают симметрии токов в питающей сети даже при одинаковой нагрузке двух плеч. При неравномерной нагрузке плеч преимущество трансформаторов Скотта не столь значительно.

Несимметричная трёхфазная система векторов тока или напряжения может быть представлена как сумма симметричных составляющих прямого обратного и нулевого следования фаз. В системе электроснабжения железных дорог ток нулевой последовательности отсутствует, так как в системе нет нулевого (нейтрального) провода. Составляющие прямого и обратного следования определяются по формулам:

(2.1)

где – составляющая прямого следования в фазе А;

– составляющая обратного следования в фазе А;

– фазный оператор (комплексный множитель):

(2.2)

Несимметрия токов характеризуется коэффициентом несимметрии:

(2.3)

где 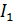– ток прямой последовательности;

–ток обратной последовательности.

Для определения коэффициента несимметрии токов по вышеприведённым формулам необходимо знать величины токов , , 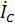и их начальные фазы. Величины токов в данной работе измеряются амперметром, а начальные фазы ψ_A, ψ_C определяются из векторной диаграммы токов (рис. 2.1). При её построении вектор можно направить произвольно, (например, горизонтально), а вектора и 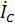построить так, чтобы сумма трёх векторов была равна нулю, причём нужно проследить, чтобы вектор опережал , а 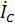– отставал от него. При таком построении ψ_B =0, а ψ_A и ψ_C определяются из рисунка с помощью транспортира.

Рис. 2.1. К определению начальных фаз токов трёхфазной питающей

сети

Углы ψ_A и ψ_A можно измерить транспортиром или рассчитать по известным длинам векторов с помощью теоремы косинусов:

(2.4)

(2.5)

(2.6)

(2.7)

Принципиальные электрические схемы

 

Рис. 3.1. Схема питания и векторная диаграмма сети с трёхфазным

трансформатором

Рис. 3.2. Схема питания и векторная диаграмма сети с двумя однофаз-

ными трансформаторами, соединёнными в открытый

треугольник

 

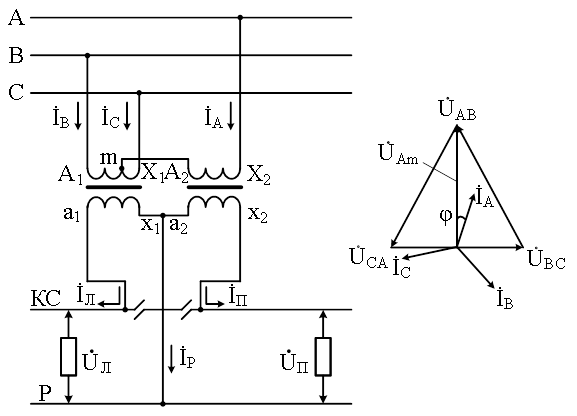
Рис. 3.3. Схема питания и векторная диаграмма сети с двумя однофаз-

ными трансформаторами, соединёнными по схеме Скотта

 

Результаты измерений

Таблица 4.1 – Токи, потребляемые от сети, при различных типах транс-

форматоров

Нагрузка плеч питания	Трёхфазный трансформатор	Схема открытого треугольника	Трансформатор Скотта
IЛ, A	IП, A	β=IЛ/IП	IA, A	IB, A	IC, A	IA, A	IB, A	IC, A	IA, A	IB, A	IC, A
		0,5

5. Результаты расчётов

Расчёт симметричных составляющих и коэффициента несимметрии будем производить в Mathcad-программе, следуя указаниям Приложения в Руководстве по выполнению базовых экспериментов ЭСЖД1-ПЕТ РБЭ (969.1).

В качестве примера рассчитаем симметричные составляющие и коэффициент несимметрии для схемы питания с трёхфазным трансформатором.

Зададим потребляемые от сети токи, полученные в результате экспериментальных измерений:

Рассчитаем углы с помощью теоремы косинусов:

Найдём начальные фазы и длины векторов токов для построения их диаграмм:

 

Рассчитаем несимметричные составляющие токов прямого и обратного следования фаз соответственно:

Определим коэффициент несимметрии для данного случая:

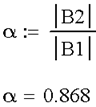
Расчёт для других схем питания сети будем вести аналогично. Полученные значения занесём в табл. 5.1.

 

 

 

Таблица 5.1 – Симметричные составляющие и коэффициенты несимметрии при различных типах

трансформаторов и различных нагрузках плеч тяговой подстанции

β	Трёхфазный трансформатор	Схема открытого треугольника	Трансформатор Скотта
ΨA, град.	ΨС, град.	I1,A	I2, A	α	ΨA, град.	ΨС, град.	I1,A	I2,A	α	ΨA, град.	ΨС, град.	I1,A	I2,A	α
	173,277	-13,966	71,746	62,286	0,868	169,684	-83,669	72,501	52,918	0,73	168,799	-114,975	78,064	55,492	0,711
0,5	147,776	-50,946	94,984	57,408	0,604	159,426	-118,531	87,576	46,201	0,528	144,983	-107,509	100,471	29,471	0,293
	106,733	-96,019	121,385	58,725	0,484	142,189	-134,939	118,283	39,283	0,332	116,198	-121,901	125,288	4,712	0,038
	64,623	-138,439	96,344	49,904	0,518	151,165	-164,721	85,844	56,894	0,663	76,066	-143,325	94,329	35,736	0,379