Обозначение главных напряжений.

Главные напряжения принято обозначать буквой σ с цифрами 1, 2 и 3 в нижнем индексе (рисунок 6.10).

При этом наибольшее с учетом знака напряжение обозначается как σ₁ а наименьшее соответственно σ₃.

Другими словами, напряжение, расположенное на числовой оси правее других – σ₁, а то, которое левее всех σ₃.

Например, для случая объемного напряженного состояния:

Рисунок 6.10 – Главные напряжения

 

При плоском напряженном состоянии:

1. Когда оба напряжения растягивающие (рисунок 6.11).

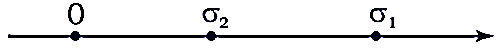
Рисунок 6.11 – Напряжения растягивающие

 

2. По одной грани напряжение растягивающее, по другой сжимающее (рисунок 6.12).

.

Рисунок 6.12 – Напряжения – растягивающие, сжимающие

 

3. Оба напряжения сжимающие (рисунок 6.13).

 

Рисунок 6.13 – Напряжения сжимающие

 

При линейном НС единственное напряжение всегда обозначается как σ₁.

 

6. Пример построения круга Мора по главным напряжениям.

Для построения круга потребуются нормальные и касательные напряжения с двух любых взаимно перпендикулярных площадок (например, правой и верхней) при этом ось σ системы направляется вдоль большего (с учетом знака) из нормальных напряжений (рисунок 6.14).

Известны направления и значения нормальных и касательных напряжений.

Рисунок 6.14 – Круг мора

 

Решение.

Круг Мора строится в плоской системе координат σ-τ (рисунок 6.15).

Начнем с правой площадки элемента. Из центра системы координат отложим вдоль оси σ значение соответствующего нормального напряжения σ_α=80Мпа с учетом его знака.

 

Рисунок 6.15 – Построение круга Мора

 

Из конечной точки отрезка отложим вдоль оси τ значение соответствующего касательного напряжения τ_α=40МПа так же с учетом знака (рисунок 6.16).

Рисунок 6.16 – Построение круга Мора

 

На конце последнего отрезка отметим точку, обозначив ее буквой A (рисунок 6.17).

Рисунок 6.17

 

Аналогично для верхней площадки элемента (рисунок 6.18).

Рисунок 6.18

 

Согласно закона парности касательных напряжений, точки A и B всегда будут расположены по разные стороны от оси σ и равноудалены от нее.

Для главных напряжений (при отсутствии касательных) точки A и B останутся на оси нормальных напряжений.

Полученные точки A и B соединяем отрезком (рисунок 6.19).

 

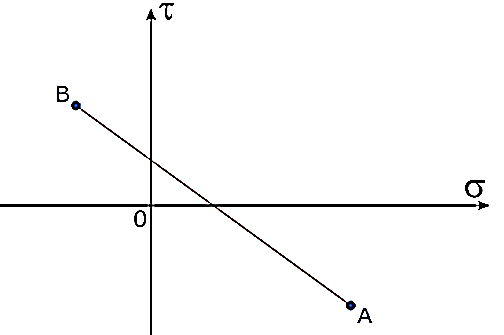
Рисунок 6.19

 

На отрезке AB как на диаметре вычерчиваем окружность, с центром в точке пересечения отрезка AB с осью σ системы координат.

Круг Мора построен.

Множество точек полученной окружности показывают величину и знак нормальных и касательных напряжений при соответствующем положении площадок элемента.

Точки пересечения круга Мора с осью σ показывают величину и знаки главных напряжений.

 

7. Пример. Определение величины и направления главных напряжений по кругу Мора.

Определить величину, знак и направление главных напряжений с помощью круга Мора по заданным нормальным и касательным напряжениям на гранях элемента (рисунок 6.20).

Рисунок 6.20 - Задача

 

Пример решения

Используем построение круга Мора в пункте 6 решения задачи (рисунок 6.21).

Рисунок 6.21

 

Как было показано ранее, координаты точек пересечения круга Мора с осью напряжений σ показывают величину главных напряжений.

В данном случае главные напряжения в точке элемента составляют

Для определения направления главных напряжений выполним следующие действия: Из точки A проводим луч влево, а из точки B вниз до пересечения (рисунок 6.22).

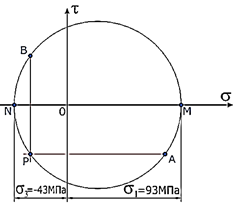
Рисунок 6.22

 

Точка их пересечения обозначается буквой P и является полюсом круга Мора. Очевидно, она будет располагаться на окружности (рисунок 6.23).

Рисунок 6.23

 

Луч, проведенный из полюса через точку М, показывает направление главного напряжения σ₁.

Так как точка M расположена в области положительных значений σ то пго правилу знаков соответствующее главное напряжение будет растягивающим (стрелка напряжения направляется от площадки) (рисунок 6.24).

Рисунок 6.24

 

Аналогично, луч [PN) показывает направление главного напряжения на смежной площадке элемента.

Расположение точки N слева от пересечения осей σ-τ указывает на то, что это напряжение сжимающее (стрелка напряжения направлена в сторону площадки).

Покажем полученные напряжения на заданном элементе (рисунок 6.25). Для наглядности, главные площадки изображаются в пределах заданного элемента.

Рисунок 6.25

 

Здесь видно, что в сечении элемента расположенном под углом φ к начальному, касательные напряжения исчезают, а нормальные изменив величину, становятся главными.

 

8. Задание.

Элемент конструкции находится под действием сил, создающих напряженное состояние (рисунок 6.25).

Требуется:

1. Определить главные напряжения.

2. Определить направление главных площадок с помощью круга Мора.

3. Определить максимальные касательные напряжения.

4. Записать обобщенный закон Гука и определить линейные отно­сительные деформации и относи­тельное изменение объема.

5. Определить полную удельную поте­нциальную энергию упругой

деформации.

Модуль продольной упругости Е и коэффициент Пуассона μ материала заданы. Исходные данные приведены в таблице 6.1 и рисунке 6.26.

Таблица 6.1 – Исходные данные

№ варианта	σХ, кПа	σУ, кПа	τХ, кПа	Е, МПа	μ
				2,0•105	0,25
				1,1•105	0,23
				1,4•105	0,24
				1,6•105	0,26
				1,8•105	0,27
				2,2•105	0,30
				0,25•105	0,17
		-		0,26•105	0,18
				2,1•105	0,28
		-		2,2•105	0,29

Рисунок 6.26 – Исходные данные

 

Контрольные вопросы

1. Виды напряженных состояний; главные площадки и главные напряжения.

2.Напряжения по наклонному сечению при линейном напряженном состоянии.

3. Касательные напряжения при напряженном состоянии.

4. Закон парности касательных напряжений.

5. Теории прочности: наибольших нормальных напряжений.

 

Литература

1. Волков А. Н. Сопротивление материалов. - М.: КолосС, 2004. - 62…65 с.

2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. - М.: Издательство Юрайт, 2013. - 27…31 с.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7

Тема. Кручение.

Тема практического занятия. Расчет вала на кручение.

Цель. Расчет вала на кручение.

 

Общие сведения

1. Кручение.

Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникают только крутящие моменты.

Причиной деформации при кручении является внешний вращающий момент, приложенный в плоскости, перпендикулярной оси бруса.

Для наглядного изображения распределения крутящих моментов вдоль оси бруса строится эпюра крутящих моментов. Крутящий момент в любом поперечном сечении численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения.

Крутящий момент считается положительным, если при взгляде со стороны сечения результирующий внешний момент, приложенный к рассматриваемой части бруса, будет направлен против часовой стрелки, и наоборот.

Условие прочности бруса при кручении заключается в том, что наибольшее возникающее в нем касательное напряжение не должно превышать допускаемого

где [τ k ] допускаемое напряжение при кручении, Па;

W_р - момент сопротивления кручению, равный для круглого сечения.

Момент сопротивления кручению.

Деформация при кручении представляет собой поворот поперечного сечения бруса вокруг оси кручения и называется углом закручивания. Требование жесткости к брусу состоит в том, что угол закручивания 1м длины бруса не должен превышать определенной величины. Угол закручивания участка бруса длиной l определяется по формуле

где GJ p – жесткость сечения при кручении.

 

2.Пример.

Вал (брус) круглого поперечного сечения (рис.1) нагружен внешними моментами: М 1= 4 кНм; М 2 = 8 кНм; М 3= 2 кНм.

Построить эпюры крутящих моментов и углов закручивания. Подобрать диаметр вала, если [τ к ] = 60 МПа, G = 8 ⋅104МПа, а = 0,4 м

Решение.

Разбиваем вал на три участка (1 – DC, 2 – CB, 3 – BA).

Значения крутящих моментов в сечениях каждого участка находим, используя метод сечений (рассекаем вал и рассматриваем правую часть, отбрасывая левую).

M к 1= − M 1= −4 кНм;

M к 2 = − M 1+ M 2 = −4 + 8 = 4 кНм;

M к 3= − M 1+ M 2 + M 3 = −4 + 8 + 2 = 6 кНм.

По найденным значениям строим эпюру крутящих моментов (рисунок 7.1).

Рисунок 7.1 – Эпюра крутящих моментов

 

Применяем расчетное уравнение на прочность при кручении

где – момент сопротивления кручению для вала круглого поперечного сечения.

Находим требуемый диаметр вала

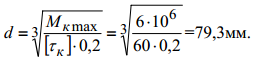
В соответствии с требованиями ГОСТ следует принять d = 80мм.

Построение эпюры угловых перемещений начинаем от заделки, т.е. от неподвижного сечения, φ A = 0

Угол поворота сечения В

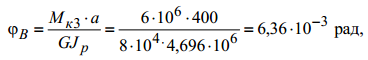
где 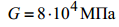-модуль сдвига;

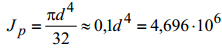- полярный момент инерции круглого сечения вала.

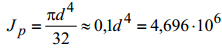
Угол поворота сечения С равен алгебраической сумме углов поворота сечения В (φ B) и сечения С относительно В (φ CB)

Угол поворота сечения D

Построенная по найденным значениям эпюра угловых перемещений показана на рисунке 7.1.

3. Задание.

Вариант 1. Для вала круглого поперечного сечения, жестко защемленного одним концом, построить эпюры крутящих моментов и углов закручивания, а также из условия прочности подобрать диаметр вала, приняв [τ к ] = 80 МПа; G = 8 ⋅104МПа. Данные для самостоятельного решения варианта задания приведены в таблице 7.1 и на рисунке 7.2.

Таблица 7.1 – Исходные данные

 

№ варианта	Внешние моменты, кНм	Длины участков, м
М 1	М 2	М 3	М 4	a	b	c	d
					0,2	0,3	0,4	0,5
				–	0,3	0,2	0,25	0,35
					0,4	0,1	0,2	0,3
				–	0,15	0,25	0,3	0,2
					0,1	0,15	0,35	0,1
				–	0,6	0,4	0,5	0,15
					0.35	0.1	0.2	0.25
				–	0,5	0,3	0,3	0,4
					0,25	0,2	0,1	0,3
				–	0,45	0,5	0,15	0,6
				–	0,2	0,4	0,5	0,35
					0.3	0,25	0,4	0,2
					0,15	0,35	0,45	0,5
				–	0,4	0,2	0,3	0,25
					0,7	0,3	0,2	0,1
					0,3	0,4	0,6	0,2
					0,25	0,5	0,3	0,4
					0,35	0,6	0,25	0,1
					0,6	0,45	0,1	0,3
				–	0,5	0,25	0,35	0,6

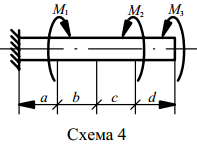
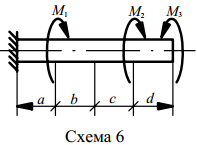
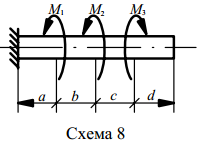
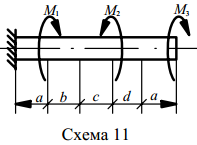
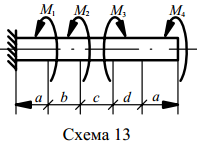
Рисунок 7.2 – Исходные данные

 

Вариант 2.

Для стального вала, нагруженного четырьмя внешними вращающими моментами (рисунок 7. 3), требуется:

1. Построить эпюру крутящего момента.

2. Определить размеры сечения сплошного вала по прочности и жесткости, округлив расчетные значения диаметров до целых миллиметров.

3. Определить размеры вала кольцевого сечения по прочности и жесткости, округлив расчетные значения диаметров до целых миллиметров. При решении задачи принять, что отношение внутреннего диаметра к внешнему диаметру для вала равно α = d/D = 0,8.

4. Сравнить массы валов сплошного и кольцевого сечений, записать вывод.

5. Построить эпюру углов закручивания сплошного вала, приняв за начало отсчета сечение, где приложен момент М₁.

Принять, что материал вала имеет модуль сдвига G = 0,8•10⁵ Мпа и расчетное напряжение на срез [τ] = 40 МПа.

Таблица 7.2 – Исходные данные

№ варианта	М1, кН•м	М2, кН•м	М3, кН•м	М4, кН•м	a, м	b, м	c, м
	2,0	3,5	1,5	5,0	0,4	0,5	0,6
	2,5	4,0	3,5	6,0	0,2	0,1	0,3
	7,0	3,5	1,0	1,5	0,3	0,2	0,1
	8,5	2,5	2,0	3,5	0,5	0,4	0,3
	4,0	2,0	2,5	1,0	0,6	0,8	0,9
	4,5	3,0	1,5	3,5	0,8	0,9	0,7
	5,0	1,5	3,0	4,5	0,7	0,6	0,5
	5,5	2,5	4,0	5,5	0,9	0,7	0,8
	6,0	2,0	0,5	7,5	0,1	0,3	0,2
	6,5	1,0	7,0	2,0	0,9	0,8	0,7

Рисунок 7.3 – Исходные данные

Контрольные вопросы

1. Примеры деформации.

2. Чистый сдвиг.

3. Деформации и напряжения.

Литература:

1. Волков А. Н. Сопротивление материалов. - М.: КолосС, 2004. - 68…77 с.

2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. - М.: Издательство Юрайт, 2013. - 232…236 с.

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8

Тема. Изгиб плоский прямой

Тема практического занятия. Определение размеров поперечного сечения консольной балки.

Цель занятия. Определить размер поперечного сечения консольной балки, нагруженной сосредоточенной силой и сосредоточенным моментом.

 

Общие сведения

1. Последовательность решения задачи.

1. Найти опорные реакции балки (для консоли их можно не находить).

2. Балку разделить на участки, границами которых являются сечения, в которых приложены: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается равномерно распределенная нагрузка.

3. Выбрать расположение координатных осей, совместив ось z с осью балки, а оси у и х расположить в плоскости сечения (обычно ось у расположена вертикально).

4. Применяя метод сечений, вычислить значения поперечных сил в характерных сечениях и построить эпюру поперечных сил. Если поперечная сила, изменяясь непрерывно, проходит через нулевое значение, то необходимо определить аппликату (z) сечения, где Q обращается в нуль.

5. Применяя метод сечений, вычислить значения изгибающих моментов в характерных сечениях и построить эпюру изгибающих моментов.

Для определения экстремальных значений изгибающих моментов дополнительно определить моменты в сечениях, где эпюра поперечных сил проходит через нулевое значение.

6. Используя дифференциальные зависимости, проверить правильность построения эпюр поперечных сил и изгибающих моментов.

7. Из условия прочности определить осевой момент сопротивления сечения балки в сечении, где изгибающий момент имеет наибольшее по модулю значение.

8. Используя таблицы ГОСТов или формулы для определения осевых моментов сопротивления простых плоских сечений (прямоугольник, круг), определить размеры поперечного сечения балки.

 

2. Задания для практического занятия.

Для стальной консольной балки построить эпюры поперечных сил и изгибающих моментов, подобрать из условия прочности необходимый размер двутавра (швеллера), приняв [ ]=160МПа. Данные своего варианта взять из таблицы 8.1 и рисунка 8.1

 

1 м F 2 м 3 м M q а)	F M 3 м 3 м q 2 м б)
Рисунок 8.1 – Исходные данные

 

Таблица 8.1 – Исходные данные

М, кН·м		-25		-10		F, кН
q, кН/м	1,2	-6	1,5	1,4	-9
№ варианта и задачи
					-20
					-30
					2,5
					-5,0

Примечание.Профиль сечения балки:

- для четных вариантов – двутавр;

- для нечетных – швеллер.

3. Пример решения.

Жестко заделанная консольная балка АВ нагружена, как показано на рис. ПЗ №4. Построить эпюры Q _y и M _x, подобрать сечение в форме двутавра.

Дано: F =20 кН; q =21 кН/м; М =28 кН∙м; [ σ ]=160 МПа.

Найти: Q _y; М _х; W _х.

Решение:

1. Изобразим балку (рисунок 8.2, а).

Рисунок 8.2 – Балка консольная

 

2. Делим балку на участки по характерным точкам: ВС, СD, DA.

3. Определяем Q _y на каждом участке и строим эпюру (рисунок 8.2, б):

- ВС, сечение I-I, слева,

0≤ z ₁≤3 м

Q _y1=0.

- СD, сечение II-II, слева,

0≤ z ₂≤2 м;

Q _y2= F =20 кН.

- DA, сечение III-III, слева,

0≤ z ₃≤2 м,

Q _y3= F-q · z ₃,

При z ₃ = 0

Q _y3= F =20 кН;

При z ₃ = 2

Q _y3= F-q ·2=20-21·2=20-42=-22 кН.

Q _y3=0

При z ₃=0,95 м.

4. Определяем М _х на каждом участке и строим эпюру (рисунок 8.2, в):

- ВС, сечение I-I, слева,

0≤ z ₁≤3 м;

М _х1= М =28 кН∙м.

- СD, сечение II-II, слева,

0<z₂<2 м,

М _х2= М - Fz₁,

При z₂=0

М _х2= М =28 кН∙м;

При z₂=2 м

М _х2= М - F· 2=28-20·2=-12 кН·м.

- DA, сечение III-III, слева,

0< z ₃<2 м,

М _х3= М-F (z ₂+2)+ qz ² /2,

При z₂=0

М _х3=28-20·2=-12 кН·м;

При z ₂=2 м

М _х3=28-20·4+21·2²/2=-10 кН·м;

При z ₂=0,95 м

М _х3=28-20·2,95+21·0,95² /2=-21,5 кН·м.

Исходя из эпюры М _х.:

ê М _{х max}ú=28 кН·м=28·10⁶ Н·мм.

5. Определяем осевой момент сопротивления сечения:

W _x ≥ê М _{х max}ú/[ σ ]; W _x≥28000000/160≥175000 мм³≥175 см³.

По ГОСТ 8239-89 выбираем двутавр № 20 с W _х=184 см³.

Ответ: W _х=184 см³ ― двутавр № 20 по ГОСТ 8239-89

 

Контрольные вопросы.

1. Какие разновидности связей используют при проектировании балок?

2. Какой изгиб называется чистым?

3. Какой изгиб называется поперечным?

4. Как определить знаки поперечной силы и изгибающего момента?

5. Как изменяется поперечная сила в сечении балки, к которому приложена сосредоточенная сила?

6. Как распределены нормальные напряжения по поперечному сечению балки?

7. Как определить нормальное напряжение в любой точке данного поперечного сечения при прямом изгибе?

8. Какие формы поперечных сечений являются рациональными для балок из пластических материалов?

 

Литература.

1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004.

2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. — М.: Издательство Юрайт, 2013.

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9

Тема. Сложное сопротивление

Тема практического занятия. Определение диаметра вала при изгибе с кручением.

Цель. Определить диаметр вала, используя гипотенузы прочности.

 

Общие сведения.

1. Последовательность решения задачи.

1. Используя принцип независимости действия сил, составить расчетные схемы вала в вертикальной и горизонтальной плоскостях.

2. Определяем реакции подшипников в горизонтальной и вертикальной плоскостях.

3 Вал разделить на участки, границами которых являются сечения, в которых приложены: сосредоточенные силы, сосредоточенные моменты. Такие сечения называются характерными.

4. Применяя метод сечений, вычислить значения изгибающих моментов в характерных сечениях в горизонтальной и вертикальной плоскостях, построить эпюры изгибающих моментов в плоскостях по отдельности.

5.Применяя метод сечений, определяем действующий на валу крутящий момент, строим его эпюру.

6. Для характерных точек определяем эквивалентные моменты, используя гипотезы прочности.

7. Из условия прочности определить моменты сопротивлений сечений вала;

8. Определяем диаметры ступеней вала.

 

2. Задания для практического занятия.

Для трансмиссионного вала (рисунок 9.1), передающего мощность Р при угловой скорости ω, необходимо:

1. Определить вертикальную и горизонтальную составляющие реакций подшипников.

2. Построить эпюры крутящего и изгибающих моментов в вертикальной и горизонтальной плоскостях.

3. Определить диаметры вала по сечениям, приняв [σ]=60 МПа и F_r =0,364 F_t. Расчет произвести, используя гипотезы прочности. На валу установлены два колеса, диаметры колес соответственно D ₁; D ₂ (рисунок 9.1).

а

а

3 а

у

х1

х

Fr 1

Ft 1

Fr 2

Ft 2

Данные своего варианта взять из таблицы 9.1.

Рисунок 9.1 – Исходные данные

 

Таблица 9.1 – Исходные данные

ω рад/с						D 1	D 2	P
a	мм
мм	кВт
№ варианта и задачи								3,0
							4,0
							5,5
							7,5
							11,5
							15,0
							18,5

 

Примечание.Расчет на прочность произвести:

- для четных вариантов – по гипотезе III;

- для нечетных – по гипотезе V.

 

3. Пример решения.

Для трансмиссионного вала, передающего мощность Р при угловой скорости ω, необходимо:

1. Определить вертикальную и горизонтальную составляющие реакций подшипников.

2. Построить эпюры крутящего и изгибающих моментов в вертикальной и горизонтальной плоскостях; определить диаметры вала по сечениям, приняв [σ]=60 МПа и F_r =0,364 F_t. Расчет провести по гипотезе III.

Дано: Р =4,2 кВт; ω =70 рад/с; а =0,1 м; D ₁=0,1 м; D ₂=0,06 м.

Найти: d

Решение I:

1. Определяем силы, действующие на колеса вала:

;

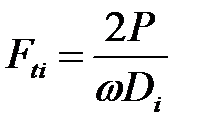=1,2 кН;

=2,0 кН;

F_{r 1}=0,364

F_{t 1}=0,364·1,2=0,44 кН;

F_{r 2}=0,364 F_{t 2}=0,364·2,0=0,73 кН.

2. Используя принцип независимости действия сил, составляем расчетные схемы вала в вертикальной и горизонтальной плоскостях (рисунок 9.2, а, б).

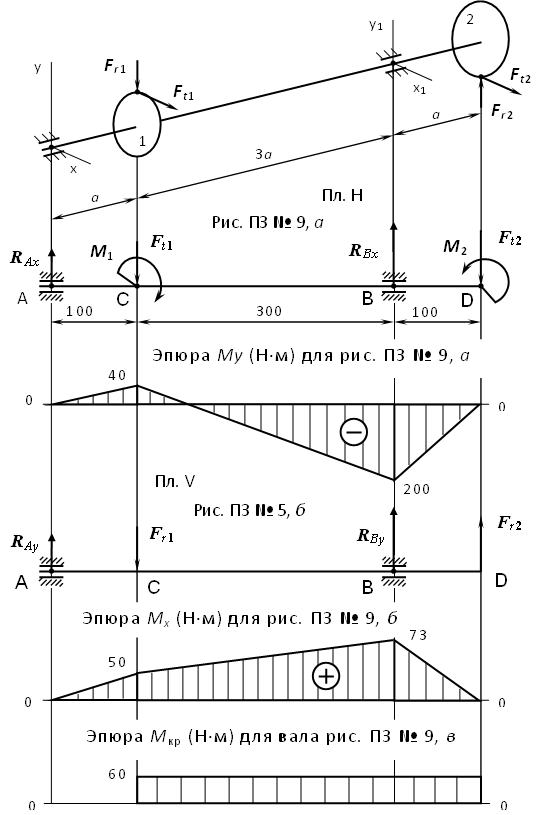
Рисунок 9.2 – Расчетная схема вала

 

3. Определяем реакции подшипников:

∑ М _у= F_{t 1}· а - R_{В х}·4 а + F_{t 2}·5 а =0;

=2,8 кН;

∑ М _у1= -F_{t 1}·3 а + R_{А х}·4 а + F_{t 2}· а =0;

=0,4 кН;

∑ М _х= F_{r 1}· а - R_{В y} ·4 а - F_{r 2}·5 а =0;

=-0,8 кH;

∑ М _x1= -F_{r 1}·3 а + R_Ау ·4 а - F_{r 2}· а =0;

=0,5 кН.

Решение II:

1. Определяем изгибающие моменты в опасных точках:

М _{х D} =0; М _{у D} =0;

Пл. Н: М _{у С} = R_{А х}· а =0,4·0,1=0,04 кН·м;

М _{у В} = -F_{t 2}· а =-2,0·0,1=-0,2 кН·м;

Пл. V: М _{х С} = R_{А у}· а =0,5·0,1=0,05 кН·м;

М _{х В} = F_{r 2}· а =0,73·0,1=0,073 кН·м.

2. Определяем крутящий момент на валу (рис. ПЗ № 9, в):

М _кр= М _вр= М ₁=| М ₂|= F_{t 1}· D ₁/2=| F_{t 2}· D ₂/2|=1,2·0,1/2=0,06 кН·м.

3. Определяем эквивалентные моменты в опасных точках по гипотезе III:

=0,09 кН·м;

=0,22 кН·м;

=0,06 кН·м.

4. Определяем диаметры вала по сечениям:

=1500 мм³; =24,8 мм;

=3667 мм³; =33,4 мм;

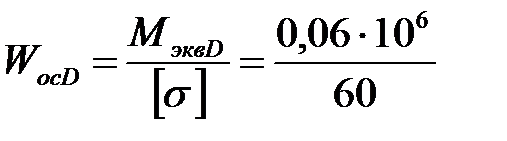=1000 мм³; =21,7 мм;

Ответ: Принимаем d_С =25 мм; d_В =35 мм; d_D =22 мм.

Контрольные вопросы.

1. Чем характеризуется и как изображается напряженное состояние в точке?

2. Какие напряжения называются главными?

3. Перечислите виды напряженных состояний.

4. Чем характеризуется деформированное состояние в точке?

5. Что такое эквивалентное напряжение?

6. Поясните назначение гипотез прочности.

7. Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения?

8. Напишите условие прочности для расчета вала.

9. Напишите формулы для расчета эквивалентного момента при расчете по гипотезе максимальных касательных напряжений и гипотезе энергии формоизменения.

10. Как выбирается опасное сечение при расчете вала?

 

Литература.

1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004.

2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-­графические работы. — М.: Издательство Юрайт, 2013.

 

 

Приложение 1