ПОЗИЦИОННЫЕ ЗАДАЧИ
Работа с геометрическими моделями, как было сказано выше, складывается из решения позиционных и метрических задач. Причем на практике чаще всего приходится иметь дело с позиционными задачами. Они являются также основой при решении метрических задач и построения теней на моделях различных объектов. Это условие определяет доминирующий характер позиционных задач в курсе начертательной геометрии. Общая характеристика и классификация позиционных задач была дана в разделе 2.
Позиционными задачами называют такие, которые позволяют определить взаимную принадлежность или неприналежность геометрических элементов друг другу или выявить третий элемент, возникающий как следствие взаимного расположения двух других элементов.
В зависимости от числа элементов, между которыми устанавливаются позиционные характеристики, все позиционные задачи делятся на две группы задач, где:
1) Выясняется взаимная принадлежность двух элементов друг другу;
2) Выявляется третий элемент как результат расположения двух данных элементов. В этой группе выделяют следующие подгруппы:
· задачи на пересечение;
· задачи на объединение элементов.
Примером первой группы задач являются задачи на определение принадлежности прямой плоскости или поверхности, принадлежности точки прямой, плоскости или поверхности. Примером второй группы позиционных задач являются задачи на пересечение прямой с плоскостью или поверхностью, пересечение поверхностей, проведение прямой через две точки или плоскости через три точки и т.п. Очевидно, что для решения задач на объединение не требуется знания специальных приёмов. Но когда дана задача на пересечение, то для поиска общего элемента двух заданных геометрических элементов необходимо выполнить специальные построения. Основными задачами этой группы являются задачи по определению точки пересечения прямой с плоскостью или поверхностью. Умение решать их позволит осуществлять решение более сложных: пересечение плоскостей и пересечение поверхностей. Причем последняя требует умения решать все остальные, которые в той или иной комбинации позволяют найти общую линию двух и более поверхностей. Следует заметить, что задачи на объединение элементов участвуют как базовые в решении всей группы задач на пересечение. В рис. 220 отражена взаимозависимость всех групп позиционных задач.
Все остальные задачи на пересечение можно представить как многократное решение этих задач. Поэтому для успешного освоения настоящего учебного курса необходимы прочные навыки в решении этих позиционных задач. Но кроме указанных знаний здесь необходимы знания всего без исключения предыдущего учебного материала. Схема, отражающая взаимосвязь дидактических единиц, способствующих освоению раздела «позиционные задачи», представлена на рис. 221.
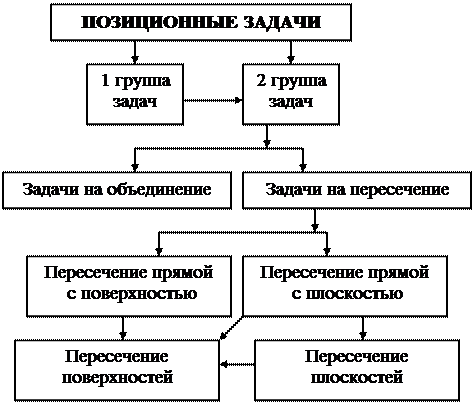 |
Рис. 220. Схема взаимозависимости позиционных задач
 |
Рис. 221. Схема, отражающая взаимосвязь дидактических единиц, влияющих на освоение раздела «позиционные задачи»
Пересечение прямой с плоскостью
В настоящем разделе рассмотрено решение одной из самых распространенных задач: пересечение прямой с плоскостью. Успех в решении этой задачи определяется, с одной стороны, умением свободно обращаться с моделями геометрических элементов, с другой стороны – знанием специальных приемов, обусловленных спецификой плоской модели.
Задача по определению общей точки прямой и плоскости встречается на практике в самых различных вариантах. Она входит как составной элемент во многие другие задачи. Поэтому ее нужно научиться решать быстро и безотказно.
В трехмерном пространстве плоскость и прямая, пересекаясь, определяют положение некоторой точки. Иное дело, когда нам дана плоская модель этих объектов (рис. 222).
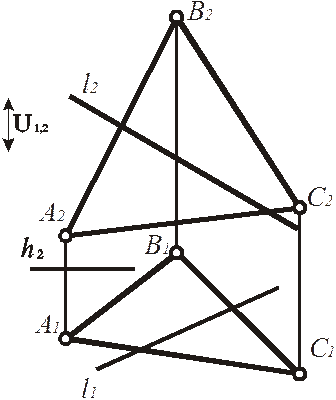
Рис. 222. Определить точку пересечения прямой с плоскостью
(перспектива)
Общая точка К прямой l и плоскости a, которая задана треугольником АВС, здесь присутствует, но не выявлена. Чтобы ее найти, нужно учесть плоский характер модели, а именно то обстоятельство, что точка на плоскости определяется как результат пересечения линий.
Одной такой линией будет заданная прямая l, другой – вспомогательная l *. Последняя возникает в результате пересечения двух плоскостей: заданной a и вспомогательной l, которая проведена через прямую l и один из центров проецирования (рис. 223, 225).
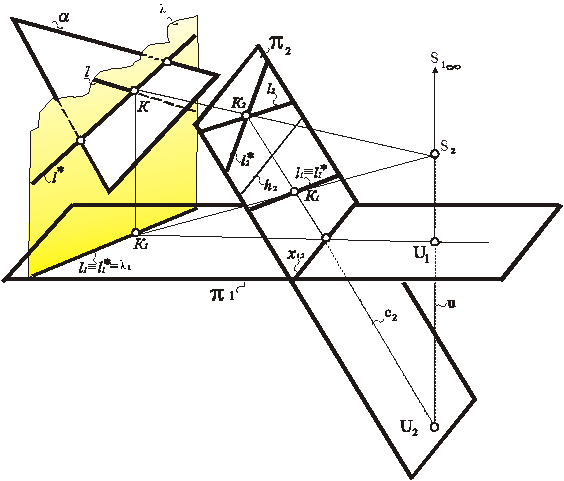
Рис. 223. Определение точки пересечения прямой с плоскостью в трехмерном пространстве
(перспектива на наклонной картине с высоким горизонтом)
Проецирующее положение плоскости l приводит к тому, что на одной из картин тождественно совпадают ее вырожденная проекция и одноименные по нижнему индексу проекции прямых l и l *. Например, на рис. 223 плоскость l содержит S1. Из чего следует: l1 º l1 º l1 *. Построив вторую проекцию l *, пересечём её с l2 и получим вторую проекцию искомой точки К = a Ç l. При необходимости можно найти и К1 (рис. 224). Для этого достаточно провести линию связи.
На рис. 225 плоскость l содержит S2. В результате ее вырожденная проекция тождественно совпадает с проекциями прямых l и l *(l2 º l2 º l2 *). Построив первую проекцию l *, пересечём её с l1 и получим первую проекцию искомой точки К = a Ç l. При необходимости можно найти и К2. Для этого достаточно провести линию связи (рис. 226).
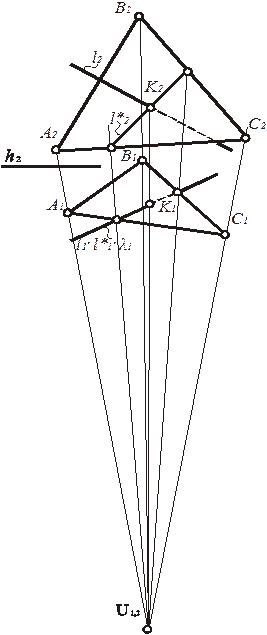
Рис. 224. Определение точки пересечения прямой с плоскостью на плоской модели (перспектива на наклонной картине с высоким горизонтом)
Таким образом, на плоской модели точка пересечения прямой с плоскостью определяется благодаря операциям, содержание которых дано в табл. 1.
Операции алгоритма по нахождению точки пересечения прямой с плоскостью
Таблица 1
| Описание операций алгоритма | Символическая запись | |
| Тождественно совмещаем одну из проекций заданной прямой с соответствующей проекцией | 
| |
| Строим другую проекцию вспомогательной прямой | 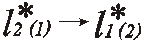
| |
| Пересекаем построенную проекцию вспомогательной прямой с одноимённой по нижнему индексу проекцией заданной прямой; в результате получаем одну проекцию точки пересечения |
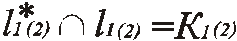
| |
| Находим другую проекцию искомой точки пересечения | 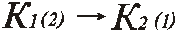
|
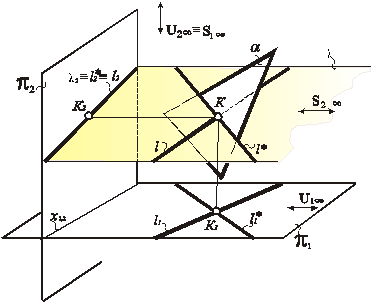
Рис. 225. Определение точки пересечения прямой с плоскостью
(эпюр Монжа)
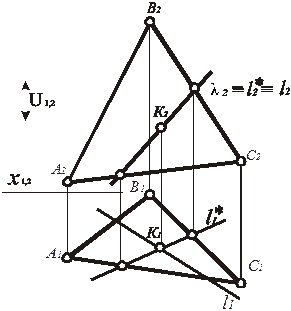
Рис. 226. Определение точки пересечения прямой с плоскостью на плоской модели (эпюр Монжа)
На рис.227 приведен пример построения общей точки проецирующей прямой l с плоскость общего положения ά (треугольник АВС). Если прямая l занимает проецирующее положение, то через нее можно провести бесконечное множество вспомогательных плоскостей, которые будут проходить через тот же центр проецирования, что и прямая. Поэтому выберем ту вспомогательную плоскость, с которой удобно работать. На рис. 227,б вспомогательная плоскость проходит через вершину А треугольника АВС, которым задана плоскость. На рис 227,а дано условие задачи, на рис. 227,б – ее решение.
Проецирующее положение заданной плоскости a (рис. 228) не меняет существо алгоритма, но существенно упрощает решение задачи. Потому что точка пересечения видна на той картине, где плоскость вырождается в прямую.
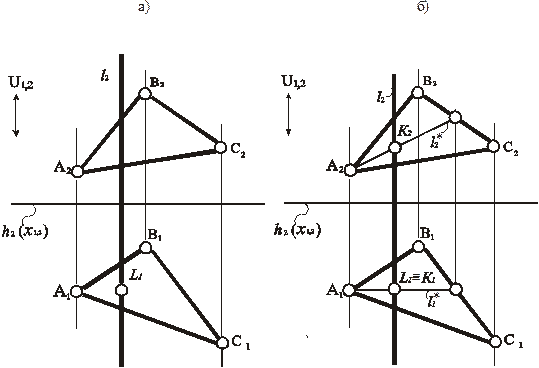
Рис. 227. Определение точки пересечения проецирующей прямой с плоскостью общего положения на плоской модели
(эпюр Монжа, перспектива на вертикальной картине)
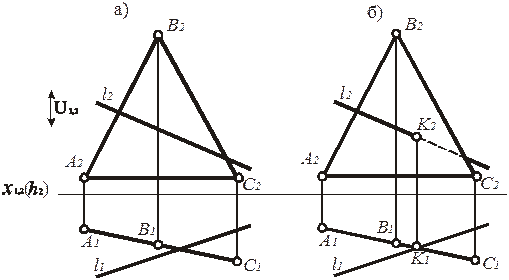
Рис. 228. Определение точки пересечения общего положения прямой с проецирующей плоскостью на плоской модели (эпюр Монжа, перспектива на вертикальной картине)






