Примеры математических моделей политического поведения

К теме выступления: Методы математического моделирования в политологии

Мангейм Дж. Б., Рич Р.К.

Политология: Методы исследования М.: Издательство “Весь Мир”, 1997. – 544 с.

ЗАЧЕМ НУЖНЫ МОДЕЛИ?

Как указывалось выше, существует множество причин, в силу которых политологи прибегают к использованию математических моделей. Однако у данного метода есть и недостатки и преимущества. Моделирование – это процесс упрощения и дедуктивного вывода. Упрощение влечет за собой потерю информации о событии. Дедуктивный вывод зачастую включает в себя сложную математическую обработку, которая, по крайней мере на первых порах, затрудняет работу с моделью. Поэтому в отношении моделирования возникает резонный вопрос: а для чего нужны все эти сложности?

Первая причина, побуждающая нас к моделированию политического поведения, состоит в том, что модель помогает формализовать происходящие в обществе события. Дело в том, что политическая жизнь достаточно регулярна, для того чтобы упрощенная неформальная модель ее могла принести определенную пользу. Большая часть того, что случается в области политики, как правило, не [c.475] является совсем уж неожиданным – на самом деле наличие элемента неожиданности указывает на то, что у нас имеются априорные представления о том, как могут развиваться события, и мы в состоянии осознать факт неожиданного поворота дел. Значит, у нас в мозгу имеются своего рода ментальные модели функционирования политических систем, даже если мы ни разу не пытались выразить их эксплицитно. Математические модели как раз и помогают эксплицировать подобные неформальные модели.

В качестве примера ментальной модели можно привести следующий. Предположим, что на предстоящих президентских выборах один из кандидатов набирает 95% всех голосов. Очевидно, что это никак не противоречит ни конституции, ни устоявшимся избирательным процедурам. Однако мы будем склонны рассматривать такой факт как крайне маловероятный в силу целого ряда причин. Во-первых, мы допускаем, что со стороны каждой партии наберется достаточное число избирателей, чтобы свести к минимуму возможность чисто случайного результата голосования. Во-вторых, мы исходим из того, что ни одна партия не станет выставлять столь непопулярного кандидата, чтобы он мог собрать лишь 5% голосов. В-третьих, мы полагаем, что подсчет голосов производится без подтасовок. Можно было бы перечислять и далее, но суть в том, что относительно политической системы США у нас имеется целый ряд исходных допущений, в свете которых разбиение голосов на 5 и 95% представляется нам малоправдоподобным.

Все подобные допущения упрощают действительность. Мы не знаем, каково точное число избирателей, да нам это и не надо – мы просто знаем, что оно очень велико. Мы не знаем, какие конкретно особенности кандидата делают его приемлемым для одних избирателей и неприемлемым для других, но мы исходим из того, что совсем уж непопулярные кандидаты не будут выдвинуты на голосование. Мало у кого есть личный опыт в деле подсчета голосов, достаточный для того, чтобы знать, честно ли проводятся выборы, но весь опыт прошлого дает основания считать, что фальсификации на выборах места не имеют ². Поскольку эти допущения не столь уж часто приводят нас к неверным выводам, мы можем использовать эту модель [c.476] политической системы для неформального прогнозирования будущего. В действительности те случаи, когда какой-либо кандидат получает 95% голосов, вызывают у населения сильное недоверие, иногда вплоть до требований о расследовании, так что наша модель отчасти определяет также поступки и отношения людей.

Другой причиной применения математического моделирования является необходимость эксплицитно описать механизмы, объясняющие наши неформальные прогнозы. Несмотря на то, что все индивиды знают, чего можно, а чего нельзя ожидать от данной политической системы, они зачастую не в состоянии определить точно, почему и что конкретно они от нее ожидают. Формальная модель как раз и помогает преодолеть чересчур свободные формулировки допущений неформальной модели и дать точный, а подчас и поддающийся проверке прогноз.

Вышеприведенный пример выводится из модели Даунса, которую мы будем рассматривать ниже в данной главе. Формальная модель Даунса предсказывает, что любая политическая партия в условиях альтернативных выборов будет выбирать своих кандидатов и платформу так, чтобы привлечь с их помощью как можно большее число избирателей. Это и некоторые дополнительные соображения приводят нас к заключению, что существует тенденция, в соответствии с которой политические партии должны получить на выборах примерно равное число голосов; именно такой исход обыкновенно и наблюдается на выборах в США. Таким образом, данная формальная модель предсказала не только то, что исход с распределением голосов в соотношении 95:5 является маловероятным, но и то, что ожидаемым будет распределение в соотношении 50:50, в пользу чего было приведено определенное обоснование.

Порой, кажется, что математические модели всего лишь подтверждают и так очевидные вещи. На самом деле это неотъемлемая особенность любых моделей постольку, поскольку от них ожидается, что они в той или иной степени должны воспроизводить все происходящее в каждодневной политической реальности. Однако люди, как правило, очень смутно представляют себе, что такое “очевидное”. Рассмотрение ряда противоречащих друг другу афоризмов (“волк волка чует издалека” и “крайности сходятся”, “с [c.477] глаз долой – из сердца вон” и “чем дальше с глаз, тем ближе к сердцу” и т.п.) убеждает нас в том, что здравый смысл часто оказывается правильным именно потому, что он настолько расплывчат, что попросту не может быть неверным.

Строгость формальных моделей, напротив, означает как раз то, что они могут быть неверными, и в результате у модели “спортивные показатели” могут быть подчас хуже, чем у более неоднозначного здравого смысла. Однако это вовсе не слабость, а, наоборот, достоинство моделирования, ибо допущения и прогнозы модели оказываются достаточно точными, чтобы их можно было проверить, а также указать, в каком месте и как произошла возможная ошибка. Та модель, которая устояла против целого ряда попыток ее искажения, вполне вероятно, и в будущем будет давать правильные прогнозы. Модель же, которая раз за разом дает неверные предсказания, видимо, должна быть устранена из рассмотрения.

Короче говоря, модель бывает полезной только в том случае, если в принципе, возможно, продемонстрировать ее ошибочность. Если невозможно показать, что модель неверна, то невозможно также доказать, что она верна, а отсюда следует вывод о бесполезности такой модели. Неформальная интуитивная модель, позволяющая уходить от всевозможных ошибок, может быть большим тактическим подспорьем на переговорах, но она бессильна помочь нам яснее понять механизм политического поведения.

Третьим преимуществом формальных моделей, но сравнению с голой интуицией или даже с тщательно обоснованной аргументацией на естественном языке является их способность систематически оперировать с сущностями более высокого уровня сложности. Естественные языки (подобно английскому) возникли как средства общения, а не как средства логического вывода. Математика, напротив, изначально была задумана как средство логического вывода и систематического оперирования понятиями. И опыт показал, что математика в этом отношении – очень полезное орудие. Политологи со своей стороны только сейчас начинают осознавать, что может дать моделирование для более углубленного понимания политического поведения, а в ряде случаев должны были развиться целые отрасли математики (самый заметный пример – [c.478] теория игр), прежде чем обществоведы смогли увидеть нечто общее в разрозненных типах социального поведения. Математическое моделирование социального поведения насчитывает не более 20 лет от роду, и пока нет оснований считать, что оно уже достигло пределов своего развития.

ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПОЛИТИЧЕСКОГО ПОВЕДЕНИЯ

Пример 2. Игра “дилемма заключенного”

 

Одна из наиболее развитых областей математического моделирования социального поведения называется теорией игр. “Игры” в рамках данной теории – это ситуации, в которых два (или более) участника делают выбор в отношении своих действий и выигрыш каждого участника зависит от совместного выбора обоих (всех). Примерами этого типа ситуаций могут служить такие традиционные игры, как шахматы, покер и футбол, поскольку исход их зависит от совокупных действий игроков. Игры, изучаемые теорией игр, обычно более формализованы, чем традиционные, и вознаграждения в них представляют собой не просто выигрыш или проигрыш, а нечто более сложное, но принцип соревнования и здесь и там один и тот же. Теория игр была разработана во время второй мировой войны и изначально рассматривалась как секретное оружие, однако с той поры она давно превратилась в самостоятельную отрасль математики.

Теория игр первоначально разрабатывалась на материале одного из типов соревнования, который носит название игры с нулевой суммой и заключается в том, что, сколько один игрок выигрывает, столько же другой проигрывает. К этой категории принадлежит большинство обычных игр, а также некоторые из “игр”, с которыми мы встречаемся в области политики, например выборы.

Однако большая часть политических ситуаций являются играми с ненулевой суммой, или кооперативными, когда оба игрока при определенных условиях могут [c.486] оказаться в выигрыше (т.е. тот факт, что один из игроков выиграл, вовсе не означает, что другой столько же проиграл). Из кооперативных игр лучше всего изучена игра “дилемма заключенного”, вариант которой разбирается ниже.

Представим себе ситуацию позиционной войны во время первой мировой войны. Солдаты британских и германских войск сидят в окопах друг против друга, разделенные только нейтральной полосой, а снайперы на брустверах выжидают, когда какой-нибудь неосторожный солдат встанет на секунду во весь рост в обстреливаемом месте, чтобы убить его. В самом начале подобного патового положения потери обеих сторон от снайперских выстрелов велики, и обе стороны чувствуют себя скованно и неуютно, будучи полностью привязанными к окопам. Но со временем, когда одни и те же подразделения неделю за неделей привыкают друг к другу, урон от снайперских атак начинает сходить на нет, постепенно приобретая характер просто несчастного случая. Посторонние наблюдатели, посещающие линию фронта, бывают удивлены, видя, как с обеих сторон солдаты расхаживают не таясь, совершенно без всякого прикрытия и никто никого не пытается при этом убить. Это совсем непохоже на то, как изображают войну в кино, и такое положение бесит некоторых офицеров, но “сотрудничество” становится правилом, и те неопытные офицеры, которые стараются заставить солдат нарушить это правило, имеют скверное свойство погибать от несчастного случая. Надо заметить, что подобное неформальное перемирие происходит без каких-либо открытых договоренностей между враждующими сторонами.

Вышеописанное представляет собой вовсе не плод выдумки пацифиста, а реальную ситуацию. Роберт Аксельрод приводит такую цитату из мемуаров британского офицера, участвовавшего в первой мировой войне: “Я пил чай в компании, когда мы услышали крики и вышли наружу узнать, в чем дело. Мы увидели, как германские и наши солдаты стоят друг против друга на своих брустверах. Внезапно рядом разорвался снаряд, но не причинил никому вреда. Естественно, обе стороны поспрыгивали в окопы, и наши стали ругать немцев, и вдруг один смелый немец вскочил на бруствер и крикнул: "Нам очень жаль, мы надеемся, никто не пострадал. Это не наша вина, это проклятая прусская артиллерия!"” ⁴.

Это явление может быть объяснено с помощью очень широко применяемой модели под названием игра [c.487] “дилемма заключенного”. В “дилемме заключенного” обе стороны стоят перед выбором: либо сотрудничать друг с другом, либо друг друга обманывать. В том примере, который мы привели, платежная матрица (в терминах количества человек, убиваемых ежедневно) могла бы выглядеть так, как это показано в табл. 17.1. В этой матрице выплаты приводятся в таком порядке: британская сторона, германская сторона – и обозначают среднее число солдат, убиваемых за день.

 

Таблица 17.1

 

Британская сторона	Германская сторона
Сотрудничество	Обман
Сотрудничество Обман	Клетка 1 –1, –1 Клетка 3 0, –10	Клетка 2 –10, 0 Клетка 4 –3, –3

 

Стратегия сотрудничества означает отсутствие намеренных попыток убить солдата противной стороны; стратегия обмана означает наличие таких попыток. Если обе стороны сотрудничают (клетка 1), то мы принимаем потери за величину случайную, что в среднем может выражаться в гибели одного солдата в день с каждой стороны. Если обе стороны намеренно ведут снайперский отстрел (клетка 4), то смертей будет больше, но ненамного, потому что обе стороны будут укрываться в окопах и не станут выставляться в качестве мишеней. И, наконец, если одна сторона начинает вести снайперский отстрел, в то время как другая занимается сотрудничеством (клетки 2 и 3), то та сторона, которая пытается сотрудничать, понесет значительные потери, а другая предположительно будет готова к отпору и вообще не понесет потерь в этот день.

В “дилемме заключенного” интересно то, что, чем хуже каждая из сторон думает о другой, тем скорее обе они примут стратегию обмана. Если одна из сторон выбирает сотрудничество, то наихудший исход (10 смертей) может ожидаться тогда, когда другая сторона в ответ выберет обман. Если одна из сторон выбирает обман, то неблагоприятный исход ожидается и тогда, когда другая сторона так же выберет обман, но это приведет всего лишь к трем смертям. Поэтому если выбирать из худших исходов [c.488] наилучший (это называется минимаксным решением), то надо обманывать. Но при этом следует учитывать, что если бы обе стороны сотрудничали, то обе они были бы в большем выигрыше, нежели в случае взаимного обмана (то есть теряли бы каждая по одному солдату в день). В этом заключается дилемма выбора.

Приведенный пример – это всего лишь один случай из очень большого числа ситуаций, к которым применима игра “дилемма заключенного” ⁵. Другие стандартные примеры – это: обоюдный контроль над вооружениями, контроль за выполнением деловых контрактов, взаимный контроль государства и фермеров за ценами на продовольствие, соблюдение картельных соглашений, принятие решения о начале войны обычного типа и даже совместное решение студентов не готовиться особенно усердно к экзамену (поскольку требования, предъявляемые к отдельному ответу, обычно зависят от общего уровня ответов).

В отношении “дилеммы заключенного” наиболее интригующим представляется то обстоятельство, что в реальной действительности игроки чаще выбирают сотрудничество, несмотря на все факторы, подталкивающие их к обману. Для специалиста по теории игр вопрос заключается в том, почему так происходит. Вопрос этот становится особенно интересным, если учесть, что, согласно существующим исследованиям по играм с ненулевой суммой, наиболее соблазнительными для игроков свойствами обладает минимаксное решение (предполагающее обоюдный обман). В этой связи до недавнего времени оставалось неясным, каков, собственно, механизм сотрудничества (кооперации) в “дилемме заключенного”.

Ключ к решению этой проблемы лежит, по-видимому, в том, что игра носит итеративный характер – т.е. повторяется много раз, – что позволяет каждой из сторон многократно наказывать другую за обман. В серии весьма искусных опытов, проведенных в начале 80-х годов, Роберт Аксельрод показал, что простая стратегия игры “зуб за зуб” – т.е. причинение противнику всего того, что он причинил вам в предыдущем туре игры, – оказывается предпочтительной в ситуации, когда большое число игроков занято в играх типа “дилеммы заключенного”. В частности, если из двух игроков оба руководствуются стратегией “зуб за зуб”, то, начав игру с сотрудничества, они и далее [c.489] будут продолжать в том же духе. Если игрок, следующий стратегии “зуб за зуб”, встречается с игроком, склонным к обману, то это, скорее всего, приведет к их взаимному уничтожению. Следовательно, в реальной действительности, где распространены ситуации типа “дилемма заключенного”, наиболее удачливыми окажутся, скорее всего, те игроки, которые согласны сотрудничать по принципу “зуб за зуб”. В тех ситуациях, в которых не умеющие или не желающие сотрудничать игроки имеют мало шансов на выживание (как в описанной выше позиционной войне или в выполнении условий деловых контрактов), успех будет, в конечном счете, на стороне того игрока, действующего по принципу “зуб за зуб”, с которым сотрудничать вполне безопасно. Это во многом объясняет, почему сотрудничество реально существует в мире, где нет ни принуждения к выполнению контрактов, ни договоренностей между игроками и где противника, пытающегося сотрудничать, выгодно обмануть.

Приведенный пример всего лишь в общих чертах дает представление об исследованиях Аксельрода и др. и о той обширной литературе, которая посвящена игре “дилемма заключенного”. Небольшие видоизменения в этой игре позволяют, кроме всего прочего, исследовать такие проблемы, как вопрос об осмысленности применения угроз, о преимуществах, которые можно получить от прерывания сделки или переговоров (стратегия “сжигания мостов”), о важности блефования и отвлекающих маневров, о значимости случайного поведения, а также целый ряд других характерных особенностей ситуаций состязания.

 

Пример 3. Модель Даунса

 

В начале работы сессии конгресса 99-го созыва в январе 1985 г. к присяге при вступлении в должность были приведены только 434 члена палаты представителей вместо обычных 435. Одно место по 8-му избирательному округу штата Индиана оставалось незанятым ввиду того, что ситуация, сложившаяся в предвыборной борьбе между кандидатом от демократов преподобным Фрэнсисом Макклоски и его соперником-республиканцем Ричардом Ф. Макинтайром, была близка к патовой. Согласно первоначальному подсчету, Макклоски обошел соперника только на 72 голоса (из 233 тыс. поданных бюллетеней), т.е. на [c.490] 0,03%. Окончательный подсчет, предпринятый палатой и послуживший причиной демонстративного ухода с заседания одного из депутатов-республиканцев, показал отрыв в пользу Макклоски уже только в четыре голоса, т.е. 0,0017% всех поданных голосов.

Чтобы представить этот случай в истинном свете, зададимся вопросом, какова вероятность того, что 233 тыс. избирателей, каждый из которых должен опустить в избирательную урну зеленый или красный бюллетень, сделают свой выбор так, что окончательное соотношение бюллетеней разного цвета в урне лишь на 0,03% отклонится от идеального разбиения 50:50? Даже если допустить, что всем избирателям одинаково безразлично, какого цвета бюллетень опустить в урну, – эта вероятность не превышает 0,0005 (огрубленно 1 шанс из 2000). Поэтому выборы, приближающиеся по результатам к игре вничью, следовало бы расценивать как крайне маловероятное событие. И, однако, в американской избирательной системе они совсем не так уж редки. Например, из семи президентских выборов три закончились с перевесом одного претендента над другим менее чем в 2% общего числа поданных голосов.

 

1960 г.	Кеннеди Никсон разность	34 226 731 34 108 157 118 574	(0,17 %)
1968 г.	Никсон Хамфри разность	31 785 480 31 275 166 510 314	(0,81 %)
1976 г.	Картер Форд разность	40 380 763 39 147 973 1 232 790	(1,5 %)

 

К этому можно было бы добавить много других примеров, относящихся к выборам в конгресс, в органы власти штатов и округов.

С точки зрения разработчика математических моделей, это довольно загадочное явление: почему столько результатов выборов оказываются между собой намного ближе, чем ожидалось бы даже при случайном распределении? В одной из своих работ по формальному моделированию в политологии Энтони Даунс предложил простой механизм объяснения этого феномена. [c.491]

Даунс использовал модель, впервые предложенную Хэролдом Хотеллингом в 1929 г. для объяснения того, почему бакалейные лавки в провинциальных городках, как правило, располагаются вблизи друг от друга. В качестве примера в рамках базовой модели Хотеллинга возьмем следующий. Допустим, что городок представляет собой шахтерский поселок в глубокой провинции, а ближайший магазин расположен от него в 50 милях. В поселок приезжают, чтобы открыть в нем магазины, два торговца-конкурента. Из опыта торговли в шахтерских поселках оба они одинаково хорошо знают, какие товары будут здесь пользоваться спросом, поэтому единственное, чем их магазины могут различаться, – это месторасположение, потому что клиенты-шахтеры, очевидно, предпочтут посещать тот магазин, который находится ближе. В подобном случае существует только одно место, идеально подходящее для расположения магазина, – это точка, в которой среднее расстояние от дома каждого шахтера до магазина является минимальным. Если оба владельца магазинов это осознают, то они расположат свои лавки в одном и том же месте, несмотря на то, что они окажутся впритык друг к другу, и, добавим мы, несмотря на то, что расположение лавок вдали друг от друга сократило бы время, необходимое части клиентов, чтобы дойти от дома до лавки, и притом сохранило бы возможность для владельцев лавок поровну поделить между собой объем коммерции (кстати сказать, это последнее соображение являет собой еще один пример “дилеммы заключенного”).

Логику модели Хотеллинга Даунс применил к ситуации выборов. В простейшей модели Даунса предполагается, что избиратели упорядочены соответственно своим политическим мнениям – от либералов до консерваторов (как показано на рис. 17.3). Предполагается также, что каждый избиратель будет голосовать за того кандидата, который идеологически ему ближе. В подобной ситуации кандидаты будут стремиться быть идеологически как можно ближе к “золотой середине” (точка, помеченная на рисунке буквой С). Если один кандидат займет центристскую позицию (точка С), а другой кандидат займет позицию, отличную от центристской (скажем, соответствующую точке О), то последний проиграет на выборах: ведь за кандидата, занимающего точку С, проголосует более 50% [c.492] избирателей, расположенных вправо от С, затем голоса распределятся в промежутке от С до О и, таким образом, это будет означать победу данного кандидата на выборах. Это саморегулирующийся процесс: кандидат может его проигнорировать, но только ценой своего провала на выборах. Поэтому следует думать, что опытные политики – те, которые уже неоднократно одерживали победу на выборах, – обладают способностью вычислять или угадывать, где расположена политическая “золотая середина”.

 

 

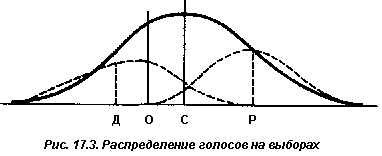
Эта модель объясняет то важное наблюдение, что на многих выборах голоса разбиваются почти пополам: ведь опытные кандидаты будут стараться быть как можно ближе к центру голосования. Однако модель Даунса предсказывает, что у кандидатов при этом будут почти одинаковые позиции, а это вовсе не обязательно так. Кандидаты на выборах в США по большей части очень близки идеологически, но все же редко настолько близки, насколько это предполагается данной моделью. Поэтому надо посмотреть, не нуждается ли модель в каких-то дополнительных допущениях.

К этой проблеме можно подходить с разных сторон, но простое наблюдение свидетельствует о том, что в большинстве округов каждый кандидат должен пройти два тура выборов – первичный и всеобщий. На первичных выборах распределение идеологических акцентов отклоняется от точки центра. Пунктирные линии на рис. 17.3 показывают гипотетическое распределение голосов в первичных турах отдельно республиканской и отдельно демократической партии: голоса на республиканских первичных выборах обычно сдвинуты сильно вправо, а на демократических – сильно влево, притом, что многие центристски настроенные избиратели в первичных турах вообще не участвуют. Применяя к первичному туру модель [c.493] Даунса – Хотеллинга, мы видим, что для того, чтобы победить, каждый кандидат будет стремиться занять позицию в центре голосов, отданных его партии (на рисунке – точки Д и Р), и тем самым удалится от точки С.

Если бы избиратели не придавали значения постоянству позиции кандидата, то самым логичным для каждого кандидата было бы во время первичных выборов занимать позицию партийного центра, а затем немедленно переориентироваться, заняв точку общеэлекторатного центра С. Однако избиратели не столь забывчивы, поэтому кандидатам приходится, двигаясь в сторону центра, не отрываться и от своей первоначальной позиции, чтобы их не обвинили в неустойчивости взглядов. Более того, в том случае, если позиция партийного центра и позиция общеэлекторатного центра разделены значительным расстоянием, кандидат, избранный на первичных выборах, может оказаться просто не в состоянии занять выигрышную позицию на всеобщих выборах и проиграет с большим отрывом от соперника (как это случилось, например, с Барри Голдуотером в 1964 г. и с Джорджем Макговерном в 1972 г.). Но в ситуации, когда оба кандидата изначально сильно удалены от центра, они вполне могут расщепить итоги голосования почти точно надвое, выбрав соответствующие симметрично расположенные относительно точки С, но при этом несовпадающие позиции. Как на то указывает частота выборов с исходом голосования 50:50, американские политики, по-видимому, очень хорошо умеют выбирать именно такие позиции.

Представленная здесь модель являет собой всего лишь простейший вариант модели Даунса; и сам Даунс, и другие исследователи занимались разработкой более сложных вариантов, чем этот. В реальной жизни мнения избирателей не поддаются строгому упорядочению в виде колоколообразной кривой, проходящей вдоль единой фиксированной идеологической оси; вместо этого они занимают меняющиеся позиции на целом ряде осей, а по некоторым вопросам занимают сильно отличные друг от друга позиции. Однако даже столь простая модель позволяет объяснить, почему некоторые, но не все выборы кончаются с исходом голосования почти 50:50, почему кандидаты не занимают на всеобщих выборах совпадающих позиций и почему кандидаты часто меняют свои [c.494] идеологические позиции в промежутке между первичными и всеобщими выборами.