Статистична обробка результатів

Для перевірки адекватності моделі розраховують число степенів вільності

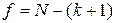, (2.8)

де ­ число коефіцієнтів математичної моделі.

Далі знаходять залишкову дисперсію, або дисперсію адекватності

, (2.9)

де 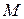– кількість повторних дослідів параметра оптимізації, , ­ – результати дослідів, середнє значення результатів дослідів.

Для перевірки гіпотези про адекватність використовується -критерій Фішера

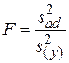, (2.10)

де ­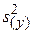 дисперсія відтворювання:

, (2.11)

Перевірка значущості кожного коефіцієнта виконується незалежно. Спочатку розраховується дисперсія коефіцієнтів

. (2.12)

Із цієї формули видно, що дисперсії всіх коефіцієнтів однакові, оскільки вони залежать тільки від помилки та кількості дослідів. Знаходять надійний інтервал

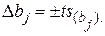(2.13)

де ­ табличне значення критерію Стьюдента, при числі степенів вільності, з якими знаходили 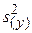табл.(Д.2)

, (2.14)

Якщо абсолютна величина коефіцієнта більша ніж величина надійного інтервалу, то коефіцієнт суттєвий.

 

Прийняття рішень після побудови математичної моделі

Адекватна математична модель, яка побудована, має вигляд полінома першого степеня. Коефіцієнти моделі – це частинні похідні функції відклику або тангенси кутів нахилу гіперплощини до відповідної осі. Більший за абсолютною величиною коефіцієнт відповідає більшому куту нахилу та більшому впливу на параметр оптимізації. Величина коефіцієнта регресії ­­­– це кількісна міра цього впливу. Знак коефіцієнта свідчить про характер впливу. Якщо знаходять максимум функції впливу, то необхідне зростання величини коефіцієнтів, знак яких від’ємний та навпаки: коли необхідно знайти максимум функції впливу, необхідне зростання величин коефіцієнтів, що мають додатний знак. У деяких задачах важливо побудувати рівняння регресії для натуральних значень факторів. У цьому випадку, використовуючи формулу (2.4), можна отримати рівняння для натуральних значень факторів, але слід мати на увазі, що коефіцієнти регресії такого рівняння будуть залежати один від одного.

 

Практичне завдання № 3

Задача. Досліджується вплив температурних і технологічних параметрів на процес виробництва деякої речовини. Вивчення процесу дозволило виділити де-кілька факторів, які суттєво впливають на процес, що вивчається:

- частота обертання механізму від 300 до 1100 хв^-1 збільшує вихід речовини (, хв.^-1);

- зростання частки каталізатора збільшує вихід речовини (, л/год);

- зростання температури від 20 до 60 ⁰С зменшує вихід речовини ( _,⁰С);

- зростання концентрації одного інгредієнта від 50 до 100 г/л збільшує вихід речовини (, г/л).

Як вихідна змінна прийнята частка виходу речовини. Необхідно знайти такі значення факторів, які забезпечать максимальний вихід речовини. Обрана така область зміни вказаних параметрів:

400 < < 1000 хв^-1; 0.5 < < 3,5 л\ч);

10 < < 60 ⁰С; 75 < < 150 г/л.

Усі необхідні дані зведені в табл. 2.3 та 2.4

Таблица 2.3

Вихідні дані для планування експерименту

Умови досліду	Позначення	Фактори
, хв-1	,л\год	,0С	,г/л
Нульовий рівень Інтервал варіювання Верхній рівень =+1 Нижній рівень = - 1

 

 

Таблиця 2.4

План та результати експерименту

Номер досліду		План експерименту	Вихідна змінна

1 +1 +1 +1 +1 +1 90,2 93,5 91,85

2 +1 -1 +1 +1 +1 86,0 87,5 86,75

3 +1 +1 -1 +1 +1 85,0 86,0 85,50

4 +1 -1 -1 +1 +1 81,0 82,0 81,50

5 +1 +1 +1 -1 +1 99,0 98,5 98,75

6 +1 -1 +1 -1 +1 96,0 94,0 95,0

7 +1 +1 -1 -1 +1 97,0 97,5 97,25

8 +1 -1 -1 -1 +1 90,2 90,0 90,1

9 +1 +1 +1 +1 -1 71,0 73,0 72,0

10 +1 -1 +1 +1 -1 66,0 67,5 66,75

11 +1 +1 -1 +1 -1 64,5 63,5 64,0

12 +1 -1 -1 +1 -1 52,0 54,0 53,0

13 +1 +1 +1 -1 -1 89,0 88,0 88,5

14 +1 -1 +1 -1 -1 80,4 80,0 80,2

15 +1 +1 -1 -1 -1 85,0 82,0 83,5

16 +1 -1 -1 -1 -1 76,5 77,0 76,5

Завдання:

1. Розрахувати коефіцієнти регресійного рівняння (2.6) для повного факторного експерименту, виконати порівняльний аналіз розрахункових значень параметрів оптимізації з експериментом, зробити перевірку адекватності математичної моделі та значущості кожного коефіцієнта регресійного рівняння. Виконати, згідно з розд. 2.4, дослідження математичної моделі та знайти область з максимальним виходом продукту.

2. Побудувати план дробового факторного експерименту 2^4-1 для випадку лінійної моделі та моделі із взаємодією для таких пів реплік, які задані визначальними контрастами та наведені нижче у табл. 2.5 (вибір варіанта узгоджується з викладачем).

3. Побудувати математичну модель, обчислити коефіцієнти регресійного рівняння та виконати порівняльний аналіз обчислюваних значень параметрів оптимізації з експериментом.

 

Таблиця 2.5

Варіанти завдань

N варіанта	Визначальний контраст	N варіанта	Визначальний контраст
1.0		2.0
1.1		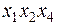2.1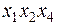
1.2		2.2
1.3		2.3
1.4		2.4
1.5		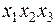2.5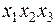
1.6		2.6
1.7		2.7
1.8		2.8

ДОДАТОК

Таблиця Д.1

Таблица значений функций

 

0,00		0,45	0,1736	0,90	0,3159	1,35	0,4115
0,01	0,0040	0,46	0,1772	0,91	0,3186	1,36	0,4131 '
0,02	0,0080	0,47	0,45	0,92	0,3212	1,37	0,4147.
0,03	0,0120	0.48	0,46	0,93	0,3238	1,38	0,4162
0,04	0,0160	0,49	0,47	0,94	0,3264	1,39	0,4177
0,05	0,0199	0,50	0.48	0,95	0,3289	1,40	0,4192
0,06	0,0239	0,51	0,49	0,96	0,3315	1,41	0,4207
0,07	0,0279	0,52	0,50	0,97	0,3340	1,42	0,4222
0,08	0,00319	0,53	0,51	0,98	0,3365	1,43	0,4236
0,09	0,0359	0,54	0,52	0,99	0,3389	1,44	0,4251
0,10	0,0398	0,55	0,53	1,00	0,34Ш	1,45	0,4265
0,11	0,0438	0,56	0,54	1,01	0,3438	1,46	0,4279
0,12	0,0478	0,57	0,55	1,02	0,3461	1,47	0,4292
0,13	0,0517	0,58	0,56	1,03	0,3485	1,48	0,4306
0,14	0,0557	0,59	0,57	1,04	0,3508	1,49	0,4319
0;15	0,0596	0,60	0,58	1,05	0,3531	1,50	0,4332
0,16	0,0636	0,61	0,59	1,06	0,3554	1,51	0,4345
0,17	0,0675	0,62	0,60	1,07	0,3577	1,52	0,4357
0,18	0,0714	0,63	0,61	1,08	0,3599	1,53	0, 4370
0,19	0,0753	0,64	0,62	1,09	0,3621	1,54	0,4382
0,20	0,0793	0,65	0,63	1,10	0,3643	1,55	0,4394
0,21	0,0832	0,66	0,64	1,11	0,3665	1,56	0,4406
0,22	0,0871	0,67	0,65	1,12	0,3686	1,57	0,4418
0,23	0,0910	0,68	0,66	1,13	0,3708	1,58	0,4429
0,24	0,0948	0,69	0,67	1,14	0,3729	1,59	0,4441
0,25	0,0987	0,70	0,68	1,15	0,3749	1,60	0,4452
0,26	0,1026	0,71	0,69	1,16	0,3770	1,61	0,4463
0,27	0,1064	0,72	0,70	1,17	0,3790	1,62	0,4474
0,28	0,1103	0,73	0,71	1,18	0,3810	1,63	0,4484
0,29	0,1141	0,74	0,72	1,19	0,3830	1,64	0,4495
0,30	0,1179	0,75	0,73	1,20	0,3849	1,65	0,4505
0,31	0,1217	0,76	0,74	1,21	0,3869	1,66	0,4515
0,32	0,1255	0,77	0,75	1,22	0,3883	1,67	0,4525
0,33	0,1293	0,78	0,76	1,23	0,3907	1,68	0,4535.
0,34	0,1331	0,79	0,77	1,24	0,3925	1,69	0,4545.
0,35	0,1368	0,80	0,78	1,25	0,3944	1,70	0,4554
0,36	0,1406	0,81	0,79	1,26	0,3962	1,71	0,4564
0,37	0,1443	0,82	0,80	1,27	0,3980	1,72	0,4573
0,38	0,1480	0,83	0,81	1,28	0,3997	1,73	0,4582
0,39	0,1517	0,84	0,82	1,29	0,4015	1,74	0,4591
0,40	0,1554	0,85	0,83	1,30	0,4032	1,75	0,4599
0,41	0,1591	0,86	0,84	1,31	0,4049	1,76	0,4608
0,42	0,1628	0,87	0,85	1,32	0,4066	1,77	0,4616
0,43	0,1664	0,88	0,86	1,33	0,4082	1,78	0,4625
0,44	0,1700	0,89	0,87	1,34	0,4099	1,79	0,4633

 

Продолжение таблицы

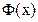
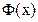
1,80	0,46410	2,00	0,4772	2,40	0,4918	2,80	0,4974
1,81	0,4649	2,02	0,4783	2,42	0,4922	2,82	0,4976
1,82	0,4656	2,04	0,4793	2,44	0,4927	2,84	0,4977
1,83	0,4664	2,06	0,4803	2,46	0,4931	2,86	0,4979
1,84	0,4671	2,08	0,4812	2,48	0,4934	2,88	0,4980
1,85	0,4678	2,10	0,4821	2,50	0,4938	2,90	0,4981
1,86	0,4686	2,12	0,4830	2,52	0,4941	2,92	0,4982
1,87	0,4693	2,14	0,4838	2,54	0,4945	2,94	0,4984
1,88	0,4699	2,16	0,4846	2,56	0,4948	2,96	0,4985
1,89	0,4706	2,18	0,4854	2,58	0,4951	2,98	0,4986
1,90	0,4713	2,20	0,4861	2,60	0,4953	3,00	0,49865
1,91	0,4719	2,22	0,4868	2,62	0,4956	3,20	0,49931
1,92	0,4726	2,24	0,4875	2,64	0,4959	3,40	0,49966
1,93	0,4732	2,26	0,4881	2,66	0,4961	3,60	0,499841
1,94	0,4738	2,28	0,4887	2,68	0,4963	3,80	0,499928
1,95	0,4744	2,30	0,4893	2,70	0,4965	4,00	0,499968
1,96	0,4750	2,32	0,4898	2,72	0,4967	4,50	0,499997
1,97	0,4756	2,34	0,4904	2,74	0,4969	5,00	0,499997
1,98	0,4761	2,36	0,4909	2,76	0,4971
1.99	0,4767	2,38	0,4913	2,78	0,4973

 

Таблиця Д.2