Задание 2 Построение графиков плотностей распределения диагностического параметра при двух диагнозах объекта.
Текст задания и исходные данные.
Техническое диагностирование объекта осуществляется по параметру К. Для исправного объекта даются среднее значение параметра К1 и среднеквадратичное отклонение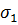 
. Для неисправного соответственно К2 и 
.
Известно, что закон распределения диагностического параметра К имеет нормальное распределение, как при диагнозе D1, так и при диагнозе D2.
Параметры распределения при диагнозе D1: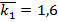 
, СКО 
Параметры распределения при диагнозе D2: 
, СКО 
Соотношение цен 
. Значения вероятностей Р1=0,9 и Р2=0,1.
Объект - газотурбинный двигатель.
Параметр - концентрация примесей меди (Сu) в масле (г/т).
Неисправное состояние – повышенная концентрация Cu в масле из-за интенсификации процессов изнашивания омедненных шлицевых соединений приводных валов.
Указания к выполнению и выполнение задания.
Для расчета точечных значений плотностей распределения использовать общую формулу дифференциальной плотности гауссовского (нормального) распределения:
(2.1)
Рекомендуется задаваемые значения К определять по правилу трех 
. Рассчитанные по формуле (2.1) значения сводятся в расчетную таблицу 2.1, после чего в виде 10 точек эти значения изображаются на масштабном поле f (k). Затем точки аппроксимируются двумя плавными кривыми (для диагнозов D1 и D2) (рисунок 2.1).
Таблица 2.1-Расчетная таблица
| № этапа | Переменные и выражения | Значения переменных (выражений) при различных ki | |||||||||||
| Для диагноза D1 | Для диагноза D2 | ||||||||||||
| 0,7 | 1,3 | 1,9 | 2,2 | 2,5 | |||||||||
| si | 0,3 | ||||||||||||
| k*i | 1,6 | ||||||||||||
| 1,330145 | 0,199522 | |||||||||||
| 4,5 | 0,5 | 0,5 | 4,5 | 4,5 | 0,5 | 0,5 | 4,5 | |||||
| 0,011109 | 0,1353353 | 0,60653066 | 0,60653066 | 0,1353353 | 0,011109 | 0,011109 | 0,1353353 | 0,60653066 | 0,60653066 | 0,1353353 | 0,011109 | |
| f(ki / Di) = (3)*(5) | 0,014777 | 0,180016 | 0,806774 | 0,806774 | 0,180016 | 0,014777 | 0,002216 | 0,027002 | 0,121016 | 0,121016 | 0,027002 | 0,002216 |
Рисунок 2.1- Графики плотностей распределения диагностического параметра при двух диагнозах объекта
Выводы.
1. Построенные графики плотности распределения показателя k для диагнозов D1 и D2 образуют две достаточно различимые группы значений.
2. Области диагнозов D1 и D2 пересекаются, поэтому принципиально невозможно определить граничное (критическое) значение k0, при котором не было бы ошибочных решений.
3. Для корректного разграничения диагнозов D1 и D2 значением k0 необходимо применение специальных методов, например, методов статических решений.
Задание 3 Оценка граничного значения Ko с использованием критерия минимального риска.
Текст задания и исходные данные:
Рассчитать граничное значение Ко с использованием решающего правила (3.1) для критерия минимального риска. Считать распределение параметра К в 1-м и 2-м диагнозах (D1 и D2) нормальным. Найденное значение Ко указать вертикальной линией на графике полученном в задании 2. Дополнительно рассчитать значения вероятности ложной тревоги 
, вероятности пропуска дефекта 
и риска 
. Использовать исходные данные задания 2.
Указания к выполнению задания:
При получении квадратного уравнения относительно искомого значения Ко, а также и использовать таблицу квантилей нормального распределения. В качестве искомого корня квадратного уравнения использовать то значение, которое располагается между значениями 
и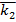 
.
Для расчета корня уравнения вида 
использовать выражение:
(3.1)
Выполнение задания:
Решающее правило записывается следующим образом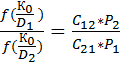 
Подставим в решающее правило выражение для плотностей 
и 
, считая, что f-плотности имеют нормальное распределение и выполнив логарифмирование (т.к.
), получим:
(3.2)
Подставим в формулу (3.2) исходные данные и преобразуем выражение для получения «стандартного» квадратного уравнения:
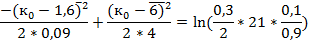
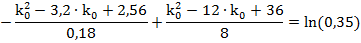
+ 25,6∙ 
(3.3)
Вычислим корни уравнения (3.2) по формуле (3.1):
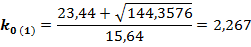
Ориентируясь на график, представленный в задании 2, выбираем граничное значение ко, которое попадает в промежуток между значениями и 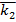. Это значение ко=2,267.
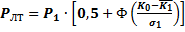(3.4)
(3.5)
R = РЛТ + (С12 / С21) ·РПД, (3.6)
По формулам (3.4, 3.5 и 3.6) рассчитаем значения вероятностей РЛТ, РПД и R:
.
.
.
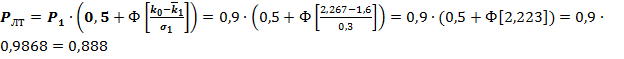Критическое значение показателя k0, полученные с помощью критерия «минимального риска», равно 2,465. В данном критерии при определении значения k0 учтены следующие факторы: цена вероятных ошибок диагностирования; статистическая точность результатов наблюдений; вероятность нахождения самолетов в различных состояниях (диагнозах).
Задание 4 Оценка граничного значения Ko с использованием критерия минимального числа ошибочных решений.
Текст задания и исходные данные:
Рассчитать граничное значение Ко с использованием решающего правила (4.1) для критерия минимального числа ошибочных решений. Считать распределение параметра К в 1-м и 2-м диагнозах (D1 и D2) нормальным. Найденное значение Ко указать вертикальной линией на графике полученном в задании 2. Дополнительно рассчитать значения вероятности ложной тревоги , вероятности пропуска дефекта и риска . Использовать исходные данные задания 2.
Указания к выполнению задания:
При получении квадратного уравнения относительно искомого значения Ко, а также и использовать таблицу квантилей нормального распределения. В качестве искомого корня квадратного уравнения использовать то значение, которое располагается между значениями и .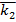
Выполнение задания:
Решающее правило записывается следующим образом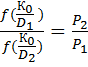 
(4.1)
Подставим в решающее правило выражение для плотностей и , считая, что f-плотности имеют нормальное распределение и выполнив логарифмирование получим:
(4.2)
Подставим в формулу (4.2) исходные данные и преобразуем выражение для получения «стандартного» квадратного уравнения:
+ 28,8∙ 
(4.3)
Вычислим корни уравнения:
Выбираем граничное значение ко, которое попадает в промежуток между значениями и 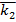. Это значение ко=2,7855.
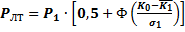(4.4)
(4.5)
R = РЛТ + (С12 / С21) ·РПД, (4.6)
По формулам (4.4, 4.5 и 4.6) рассчитаем значения вероятностей РЛТ, РПД и R:
.
.
.
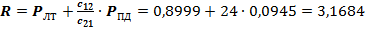Критическое значение показателя k0, полученные с помощью критерия «минимального числа ошибочных решений», равно 2,7855. В данном критерии при определении значения k0 учтены следующие факторы: статистическая точность результатов наблюдений; вероятность нахождения самолетов в различных состояниях (диагнозах).
Задание 5 Оценка граничного значения Ko с использованием критерия максимального правдоподобия
Текст задания и исходные данные:
Рассчитать граничное значение Ко с использованием решающего правила (5.1) для критерия минимального числа ошибочных решений. Считать распределение параметра К в 1-м и 2-м диагнозах (D1 и D2) нормальным. Найденное значение Ко указать вертикальной линией на графике полученном в задании 2. Дополнительно рассчитать значения вероятности ложной тревоги , вероятности пропуска дефекта и риска . Использовать исходные данные задания 2.
Указания к выполнению задания:
При получении квадратного уравнения относительно искомого значения Ко, а также и использовать таблицу квантилей нормального распределения. В качестве искомого корня квадратного уравнения использовать то значение, которое располагается между значениями и .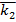
Выполнение задания:
Решающее правило записывается следующим образом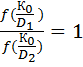 
(5.1)
Подставим в решающее правило выражение для плотностей и , считая, что f-плотности имеют нормальное распределение и выполнив логарифмирование получим:
(5.2)
Подставим в формулу (5.2) исходные данные и преобразуем выражение для получения «стандартного» квадратного уравнения:
+ 28,8∙ 
(5.3)
Вычислим корни уравнения:
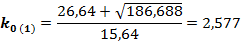
Выбираем граничное значение ко, которое попадает в промежуток между значениями и 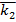. Это значение ко=2,577.
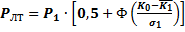(5.4)
(5.5)
R = РЛТ + (С12 / С21) ·РПД, (5.6)
По формулам (5.4, 5.5 и 5.6) рассчитаем значения вероятностей РЛТ, РПД и R:
.
.
.
Критическое значение показателя k0, полученные с помощью критерия «максимального правдоподобия», равно 2,577. В данном критерии при определении значения k0 учтены следующие факторы: статистическая точность результатов наблюдений.
Задание 6 Оценка граничного значения Ко методами итерации и Неймана-Пирсона на ЭВМ.
Текст задания и исходные данные:
По исходным данным к заданию 2, с помощью программного продукта «Модельер-А» рассчитать граничное значение Ко, вероятности ложной тревоги , вероятности пропуска дефекта и риска для обоих методов, результаты указать на графике по заданию 2. Сформировать сводную таблицу результатов по всем 5 методам и сформировать сводные выводы по заданиям 3-6. Для всех вариантов норматив принять равным 0,05. Результат Ко выполнить с точностью ξ=0,15.
Выполнение задания:
В результате расчета граничного значения Ко, вероятности ложной тревоги , вероятности пропуска дефекта и риска для обоих методов с помощью программного продукта «Модельер-А» были получены следующие результаты, сведенные в таблицу 6.1:
Таблица 6.1 Сводная таблица полученных результатов.
| №задания | Ко |
|
|
|
| 2,676 | 0,8874 | 0,0964 | 3,1046 | |
| 2,69 | 0,899955 | 0,095 | 3,085 | |
| 2,487 | 0,8962 | 0,096 | 3,1042 | |
| 2,5 | 0,016 | 0,0158 |
Рисунок 6.1 Граничные значения Ко, найденные с помощью различных критериев статистических решений.
Выводы:
1. В результате решения найдены граничные значения Ко для пяти различных методов статистических решений. Кроме того найдены вероятности ложной тревоги Рлт, вероятности пропуска дефекта Рпд и вероятности риска объявления неправильного диагноза R также для всех пяти методов статистических решений.
2. Существенное смещение Ко в сторону диагнозов D1,либо D2 обусловлено
значительной величиной отношения цен ошибок диагностирования
и значительным отличием вероятностей пребывания самолетов в состояниях D1 и D2.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КУРСОВАЯ РАБОТА
Формирование и оценка эффективности диагностических тестов,
моделирование изменения диагностических параметров,
принятие решений по режимам диагностирования
По дисциплине
ДИАГНОСТИКА АВИАЦИОННОЙ ТЕХНИКИ
Вариант - 18
Выполнил:____________________УСЕНКО А.Н
«___»__________2013 г.
Оценка:____________
Проверил:______________________ ЧОКОЙ В.З
«___»__________2013 г.
Иркутск 2013 г
