Лялин А.Е.
ДИПЛОМНЫЙ ПРОЕКТ
На тему
Комплекс лабораторных работ по ТАУ
Пояснительная записка
Киров 2009
Содержание
Введение- 5
1 Непрерывные линейные системы-- 9
1.1 Лабораторная работа «Ознакомление с программным пакетом MatLab + Simulink»- 9
1.2 Лабораторная работа «Исследование временных и частотных характеристик. Определение параметров звеньев». 46
1.3 Лабораторная работа «Исследование устойчивости и качества линейных систем управления». 50
1.4 Лабораторная работа «Исследование влияние нулей и полюсов передаточной функции на свойства системы». 57
2 Дискретные системы-- 61
2.1 Лабораторная работа «Исследование дискретных линейных систем»- 61
3 Нелинейные системы-- 65
3.1 Лабораторная работа «Исследование свойств систем на фазовой плоскости»- 65
4 Адаптивные системы-- 69
4.1 Лабораторная работа «Исследование комбинированных систем»- 69
4.2 Лабораторная работа «Исследование адаптивной системы управления»- 71
4.3 Лабораторная работа «Исследование оптимальных по быстродействию процессов»- 78
4.4 Лабораторная работа «Исследование системы экстремального управления». 81
Заключение- 86
Библиографический список-- 87
Введение
Современные средства и технологии разработки автоматизированных систем управления являются достаточно сложными, и их эффективное использование на практике, а также продвижение в направлении широкого применения, в значительной степени зависит от уровня подготовки как эксплуатационного персонала, так и инженеров-разработчиков автоматизированных систем. При этом уровень подготовки специалистов по автоматизации и телемеханике во многом определяется практическими навыками, которые могут быть получены только при работе на полнофункциональных комплексах, так как в условиях промышленного предприятия возможности обучения или повышения квалификации специалистов ограничены зачастую жестким производственным регламентом.
Следует отметить, что такой лабораторный комплекс должен обеспечить возможность как изучения отдельных компонентов и средств современных автоматизированных систем управления (технических, программных, математических, информационных), так и проведения комплекса лабораторных работ по изучению функционирования систем в целом и объектов управления и исследования, а также служить основой для решения проектных задач, в том числе задач исследования автоматизированных систем.
Данный дипломный проект ставит своей целью создания комплекса для изучения Теории Автоматического Управления (ТАУ) на примере графической среды разработки автоматизированных систем управления, а также их исследования в рамках программного пакета MatLab.
Для исследования линейных и нелинейных систем существуют множество программных средств, которые обладают разнообразными возможностями для исследований систем подобного рода. Как и у любого программного пакета у них существуют свои положительные стороны и недостатки. Кратко рассмотри возможности трех основных инструментов для исследования линейных и нелинейных систем. Это VisSim, System View и MatLab.
VisSim
Фирма Visual Solutions является производителем такого программного продукта как VisSim. VisSim - это диалоговая визуальная оболочка для разработки непрерывных, дискретных, мультичастотных и гибридных моделей систем и моделирования динамики этих систем. Набор команд, предоставляемый VisSim, позволяет автоматизировать решения многих задач.
Программа предоставляет человеку развитой графический интерфейс, используя который, исследователь создает модель из виртуальных элементов с некоторой степенью условности так же, как если бы он строил реальную систему из настоящих элементов. Это позволяет создавать, а затем исследовать и оптимизировать модели систем широкого диапазона сложности.
В VisSim модель системы сроится в виде структурной схемы в привычном виде. Основными инструментами являются функциональные блоки и связи между ними. Каждый блок выполняет определенную функцию. Функция может быть такой же простой как "sin" или сложной, как передаточная функция 10-го порядка. VisSim содержит более 100 линейных и нелинейных блоков, позволяющих моделировать сколь угодно сложные системы. Но если вдруг по каким-то причинам предоставленный набор средств окажется недостаточным, то VisSim предоставляет простой механизм расширения за счет пользовательских блоков.
Моделирование системы в VisSim означает пошаговое решение уравнений, описывающих данную систему и вычисление выходов модели. Если изменить параметры системы во время процесса моделирования, VisSim немедленно пересчитает параметры системы и учтет их при моделировании. Моделирование систем управления это далеко не весь круг задач, которые можно решать в VisSim. Например, в этой программе при желании можно решать дифференциальные уравнения и VisSim делает это значительно эффективнее и быстрее, чем известная программа математической направленности MathCAD.
При описании и последующем построении модели в среде VisSim нет необходимости записывать и решать дифференциальные уравнения, программа это сделает сама по предложенной ей исследователем структуре системы и параметрам ее элементов. Результаты решения выводятся в наглядной графической форме. Поэтому программой могут пользоваться и те, кто не имеет глубоких познаний в математике и программировании.
При использовании VisSim не требуется владеть программированием на языках высокого уровня или ассемблере. В то же время, специалисты, владеющие программированием, могут создавать собственные блоки, дополняя ими богатую библиотеку стандартных блоков VisSim.
VisSim позволяет также решать задачки по физике, начиная с уровня школьных и кончая серьезными физическими экспериментами на виртуальных лабораторных стендах.
System View
System View представляет собой полностью автономных программный пакет. Пакет System View обладает мощными интерактивными возможностями, достаточно прост и понятен. Схема моделируется с помощью основных звеньев (используемых для описания систем управления) с определенно заданными параметрами. System View удобен для пользователя как в представлении модели и результатов моделирования, так и в возможности задавать любое время исследования, стартовое время включения действия любого элемента системы, подключение различных входных воздействий. Таким образом, работая на индивидуальной рабочей станции, можно получить полное решение задачи в течении нескольких часов, причем результаты работы будут хорошо документированы (листинги, тексты, графики). Любой проектировщик или исследователь в состоянии решить свою задачу самостоятельно, без помощи программистов. Автоматизированные средства позволяют существенно увеличить эффективность анализа и проектирования систем управления. Пакет имеет обширную библиотеку типовых функциональных блоков, содержащую различные входные воздействия, передаточные функции, нелинейные зависимости и другие элементы, используемые при описании систем управления.
MatLab
Среди ряда современных СКМ (системы компьютерной математики) особо выделяется математическая система MatLab. Система MatLab предлагается разработчиками (MathWorks Inc.) как лидирующий на рынке, в первую очередь на предприятиях военно-промышленного комплекса, в энергетике, в аэрокосмической отрасли и в автомобилестроении, язык программирования высокого уровня для технических вычислений, расширяемый большим количеством прикладных программ – расширений.
Популярности MatLab способствует ее матричная ориентация и мощное главное расширение Simulink. MatLab и Simulink поставляются в виде единого программного комплекса. Они предоставляют пользователю удобные и простые средства, в том числе визуального объектно-ориентированного программирования, для моделирования линейных и нелинейных динамических систем, а также множество других пакетов расширений системы. Некоторые из них являются наиболее доступными и эффективными инструментальными средствами для развития и применения новых направлений науки и техники, таких как нечеткая логика, нейронные сети, средства анализа и обработки сигналов и изображений, средства анализа, идентификации и моделирования систем и т.п.
Структура комплекса MatLab + Simulink помимо основы – MatLab и главного расширения Simulink содержит обширные группы пакетов расширений. Этот инструментальный ящик Toolbox с числом пакетов расширения приближающимся к сотне, и группа пакетов расширения Blockset, расширяющая возможности системы визуально-ориентированного блочного моделирования динамических систем Simulink.
Одной из основных задач системы MatLab всегда было предоставление пользователям мощного языка программирования, ориентированного на технические и математические расчеты и способного превзойти возможности традиционных языков программирования, которые многие годы использовались для реализации численных методов. При этом особое внимание уделялось как повышению скорости вычислений, так и адаптивные системы к решению самых разнообразных задач пользователей.
Важными достоинствами системы являются ее открытость и расширяемость. Большинство команд и функций реализованы в в виде m-файлов текстового формата (с расширением.m) и файлов на языке Си, причем все файлы доступны для модификации. Пользователю дана возможность создавать не только отдельные файлы, но и библиотеки файлов для реализации специфических задач. Такие файлы можно готовить как в простом и удобном редакторе m-файлов системы MatLab, так и в любом другом текстовом редакторе – например Microsoft XP. C системой MatLab могут интегрироваться такие популярные математические системы, как MathCAD, Maple и Mathematica. Есть тенденция и к объединению математических систем с современными текстовыми процессорами класса MS Word. Так, средство последних версий MatLab – Notebook позволяет готовить документы в текстовом процессоре Word 98/2000/XP со вставками в виде документов MatLab и результатов вычислений, представленных в численном, табличном или графическом виде. Таким образом, становится возможным подготовка «живых» электронных книг, в которых демонстрируемые примеры могут быть оперативно изменены. Так, можно менять условия задачи и тут же наблюдать изменение результатов моделирования.
MatLab обладает хорошо развитыми возможностями визуализации двумерных и трехмерных данных. Высокоуровневые графические функции призваны сократить усилия пользователя до минимума, обеспечивая, тем не менее, получение качественных результатов. Интерактивная среда для построения графиков позволяет обойтись без графических функций для визуализации данных.
В MatLab реализованы классические численные алгоритмы решения уравнений, задач линейной алгебры, нахождения значений определенных интегралов, аппроксимации, решения систем или отдельных дифференциальных уравнений. Символические вычисления в MatLab основаны на библиотеке, являющейся ядром пакета Maple. Решение уравнений и систем, интегрирование и дифференцирование, вычисление пределов, разложение в ряд и суммирование рядов, поиск решения дифференциальных уравнений и систем, упрощение выражений – вот далеко не полный список всех возможностей MatLab для проведения аналитических выкладок и расчетов.
Программный интерфейс приложения (API) реализует связь среды MatLab с программами, написанными на Си, Fortran или Java. Библиотека программного интерфейса позволяет, вызывает имеющиеся программные модули на Си, Fortran или Java из среды или программ MatLab, обращаться к функциям MatLab из программ на Си или Fortran, осуществлять обмен данными между приложениями MatLab и другими программами.
Для разработки интернет-приложений MatLab создан MatLab Web Server, причем процесс создания приложения достаточно прост – кроме умения программировать в MatLab требуется только знание основ HTML.
Поводя итог вышесказанному, можно сделать вывод, что начинающий пользователь MatLab может в процессе работы совершенствовать свои знания как в области моделирования и численных методов, так и программирования и визуализации данных. Следует заметить еще раз, что огромным преимуществом MatLab по сравнению с другими пакетами подобного рода, является открытость кода, что дает возможность опытным пользователям разбираться в запрограммированных алгоритмах и, при необходимости, изменять их. Впрочем, разнообразие набора функций MatLab и Toolbox допускает решение большинства задач без каких-либо предварительных модификации.
При анализе программных средств, для поставленной задачи подходят все вышеописанные программные средства. Но, вследствие того, что техническое развитие постоянно заставляет использовать современное программное обеспечение, а также то, что MatLab имеет значительно больше возможностей для исследования систем автоматического управления, чем остальные, выбираем MatLab.
Исходными данными является учебная программа курса «Теория Автоматического Управления».
В главах с первой по четвертую проводится разработка проектов, на базе которых строится весь обучающий процесс. Данные проекты рассматриваются по возрастанию степени сложности и охватывают весь курс «ТАУ» начиная с непрерывных линейных систем и заканчивая адаптивными.
1 Непрерывные линейные системы
1.1 Лабораторная работа «Ознакомление с программным пакетом MatLab + Simulink»
Операционная среда Simulink
Запуск системы
Для запуска программы необходимо предварительно запустить пакет MATLAB. Основное окно пакета MATLAB показано на рисунке 1.1.1. Там же показана подсказка появляющаяся в окне при наведении указателя мыши на ярлык Simulink в панели инструментов.
Рисунок 1.1.1- Основное окно программы MATLAB
После открытия основного окна программы MATLAB нужно запустить программу Simulink. Это можно сделать одним из трех способов:
· Нажать кнопку 
(Simulink) на панели инструментов командного окна MATLAB.
· В командной строке главного окна MATLAB напечатать Simulink и нажать клавишу Enter на клавиатуре.
· Выполнить команду Open… в меню File и открыть файл модели (mdl - файл).
Последний вариант удобно использовать для запуска уже готовой и отлаженной модели, когда требуется лишь провести расчеты и не нужно добавлять новые блоки в модель. Использование первого и второго способов приводит к открытию окна обозревателя разделов библиотеки Simulink (рисунок 1.1.2).
Рисунок 1.1.2 – Обозреватель библиотеки блоков
На рисунке 1.1.2 выделена основная библиотека Simulink (в левой части окна) и показаны ее разделы (в правой части окна).
Библиотека Simulink содержит следующие основные разделы:
· Continuous – блоки аналоговых элементов;
· Discontinuities – блоки нелинейных элементов;
· Discrete – блоки дискретных элементов;
· Look – Up Tables – блоки таблиц;
· Math Operations – блоки математических операций;
· Model Verification – блоки проверки свойств сигналов;
· Model – Wide Utilities – раздел дополнительных утилит;
· Ports & Subsystems – порты и подсистемы;
· Signal Attributes – блоки задания свойств сигналов;
· Signal Routing – блоки маршрутизации сигналов;
· Sinks – блоки приема и отображения сигналов;
· Sources – блоки источника сигнала;
· User – Defined Function – функции, определяемые пользователем;
Список разделов библиотеки Simulink представлен в виде дерева, и правила работы с ним являются общими для списков такого вида:
· Пиктограмма свернутого узла дерева содержит символ " + ", а пиктограмма развернутого содержит символ " - ".
· Для того чтобы развернуть или свернуть узел дерева, достаточно щелкнуть на его пиктограмме левой клавишей мыши (ЛКМ).
При выборе соответствующего раздела библиотеки в правой части окна отображается его содержимое (рисунок 1.1.3).
Рисунок 1.1.3 – Содержимое раздела библиотеки
Создание модели
Создать новый файл модели с помощью команды File/New/Model, или используя кнопку 
на панели. Вновь созданное окно модели показано на рисунке 1.1.4.
Рисунок 1.1.4 - Пустое окно модели
1. Расположить блоки в окне модели. Для этого необходимо открыть соответствующий раздел библиотеки (Например, Sources - Источники). Далее, указав курсором на требуемый блок и нажав на левую клавишу “мыши” - “перетащить” блок в созданное окно. Клавишу мыши нужно держать нажатой.
2. Для удаления блока необходимо выбрать блок (указать курсором на его изображение и нажать левую клавишу “мыши”), а затем нажать клавишу Delete на клавиатуре.
Основные приемы подготовки и редактирования модели
Добавление текстовых надписей
Для создания надписи нужно указать мышью место надписи и дважды щелкнуть левой клавишей мыши. После этого появится прямоугольная рамка с курсором ввода. Аналогичным образом можно изменить и подписи к блоками моделей. На рисунке 1.1.5 показаны текстовая надпись и изменение надписи в блоке передаточной функции.
Рисунок 1.1.5 – Окно с текстовыми надписями
Выделение объектов
При создании и редактировании модели нужно выполнять такие операции, как копирование или удаление блоков и линий. Для этого предварительно необходимо выделить один или несколько блоков и линий (объектов).
Чтобы выделить отдельный объект, нужно щелкнуть на нем мышью один раз. В результате по углам выделенного блока или в начале и конце линии появятся маленькие квадратные черные метки. При этом все другие ранее выделенные объекты станут невыделенными.
Чтобы выделить несколько объектов, выбранных произвольно, необходимо нажать клавишу [Shift] и, удерживая её нажатой, выполнить щелчки на каждом выделяемом объекте. Затем клавишу [Shift] отпустить.
Группу объектов можно выделить также с помощью рамки. Для этого необходимо установить курсор мыши в точку, которая будет являться начальной точкой рамки, нажать левую кнопку мыши и, не отпуская её, переместить мышь в направлении диагонали прямоугольника. В результате на экране появится прямоугольная рамка и, когда кнопка мыши будет отпущена, все объекты и линии, охваченные рамкой, будут выделены.
Если требуется выделить всю модель, то есть все объекты в активном окне блок-схемы, следует воспользоваться командой Select All (выбрать всё) из меню Edit (правка) или комбинацией клавиш [Ctrl+A].
Копирование и перемещение блоков в буфер хранения
Для копирования объекта в буфер его необходимо предварительно выделить, а затем выполнить команду Edit/Copy или воспользоваться инструментом 
на панели инструментов.
Для вырезания объекта в буфер его необходимо предварительно выделить, а затем выполнить команду Edit/Cut или воспользоваться инструментом 
на панели инструментов. При выполнении данных операций следует иметь в виду, что объекты помещаются в собственный буфер MATLAB и недоступны из других приложений. Использование команды Edit/Copy model to Clipboard позволяет поместить графическое изображение модели в буфер Windows и, соответственно, делает его доступным для остальных программ.
Копирование можно выполнить и таким образом: нажать правую клавишу мыши, и не отпуская ее, переместить объект. При этом будет создана копия объекта, которую можно переместить в необходимое место.
Для вставки объекта из буфера необходимо предварительно указать место вставки, щелкнув левой клавишей мыши в предполагаемом месте вставки, а затем выполнить команду Edit/Paste или воспользоваться инструментом 
на панели инструментов.
Удаление блоков
Для удаления объекта его необходимо предварительно выделить, а затем выполнить команду Edit/Clear или воспользоваться клавишей Delete на клавиатуре. Следует учесть, что команда Clear удаляет блок без помещения его в буфер обмена. Однако эту операцию можно отменить командой меню File/Undo.
Соединение блоков
Для соединения блоков необходимо сначала установить курсор мыши на выходной порт одного из блоков. Курсор при этом превратится в большой крест из тонких линий (рисунок 1.1.6). Держа нажатой левую кнопку мыши, нужно переместить курсор ко входному порту нужного блока. Курсор мыши примет вид креста из тонких сдвоенных линий. После создания линии необходимо отпустить левую клавишу мыши. Свидетельством того, что соединение создано, будет жирная стрелка у входного порта блока. Выделение линии производится точно также как и выделение блока – одинарным щелчком левой клавиши мыши. Черные маркеры, расположенные в узлах соединительной линии будут говорить о том, что линия выделена.
Рисунок 1.1.6 – начало создания соединения
Создание петли линии соединения выполняется также как перемещение блока. Линия соединения выделяется, и затем нужная часть линии перемещается. Рисунок 1.1.7 поясняет этот процесс. Удаление соединений выполняется также как и любых других объектов.
Рисунок 1.1.7. – создание петли в соединительной линии
Деление линии на сегменты
При необходимости линию можно разделить на два сегмента. Для этого следует выполнить следующие действия:
· выделить линию и установить курсор в точку излома линии;
· нажать клавишу [Shift] и левую кнопку мыши; курсор при этом примет форму окружности, а на линии образуется излом;
· переместить курсор (излом) в новое положение;
· отпустить клавишу [Shift] и кнопку мыши.
Результат этих действий представлен на рисунке 1.1.8, где линия, соединяющая блоки «Step» и «Scope», разделена на несколько сегментов
Рисунок 1.1.8 – деление линии на сегменты
Изменение размеров блоков
Для изменения размера блока он выделяется, после чего курсор мыши надо установить на один из маркеров по углам блока. После превращения курсора в двустороннюю стрелку, необходимо нажать левую клавишу мыши и растянуть (или сжать) изображения блока. На рисунке 1.1.9 показан этот процесс. Размеры надписей блока при этом не изменяются.
Рисунок 1.1.9 – Изменение размера блока
Перемещение блоков и вставка блоков в соединение
Любой блок модели можно переместить, выделив его, и передвинув, держа нажатой левую клавишу мыши. Если ко входам и выходам блока подведены соединительные линии, то они не разрываются, а лишь сокращаются или увеличиваются в длине. В соединение можно также вставить блок, имеющий один вход и один выход. Для этого его нужно расположить в требуемом месте соединительной линии.
Форматирование объектов
В меню Format (также как и в контекстном меню, вызываемом нажатием правой клавиши мыши на объекте) находится набор команд форматирования блоков. Команды форматирования разделяются на несколько групп:
1. Изменение отображения надписей:
Font — Форматирование шрифта надписей и текстовых блоков;
Text alignment — Выравнивание текста в текстовых надписях;
Flip name — Перемещение подписи блока;
Show/Hide name — Отображение или скрытие подписи блока.
2. Изменение цветов отображения блоков:
Foreground color — Выбор цвета линий для выделенных блоков.
Background color — Выбор цвета фона выделенных блоков.
Screen color — Выбор цвета фона для всего окна модели.
3. Изменение положения блока и его вида:
Flip block – Зеркальное отображение относительно вертикальной оси симметрии.
Rotate block – Поворот блока на 900 по часовой стрелке.
Show drop shadow — Показ тени от блока.
Show port labels — Показ меток портов.
4. Форматирование надписей
Команда Format/Font выводит окно с установками шрифта для текстовых надписей, позволяющие изменять вид шрифта надписи, размер шрифта, начертание и т. п. параметры надписи.
5. Прочие установки:
Library link display — Показ связей с библиотеками.
Sample time colors — Выбор цвета блока индикации времени.
Wide nonscalar lines — Увеличение/уменьшение ширины линий векторных сигналов.
Signal dimensions — Показ размерности сигналов.
Port data types — Показ данных о типе портов.
Storage class — Класс памяти. Параметр, устанавливаемый при работе Real-Time Workshop.
Execution order — Вывод порядкового номера блока в последовательности исполнения.
Создание и манипулирование метками сигналов
Чтобы создать метку сигналов, нужно дважды щелкнуть на сегменте линии и затем ввести текст метки. Двойной щелчок следует выполнять точно на линии, т.к. в противном случае будет создан комментарий к модели.
Перемещение метки осуществляется путём перетаскивания её мышью на новое место. Если при этом удерживать нажатой клавишу [Ctrl], то метка будет скопирована в новое место. Скопировать метку можно также, выполнив двойной щелчок на другом сегменте линии.
Чтобы отредактировать метку, следует щелкнуть на ней правой кнопкой мыши и затем внести соответствующие изменения в ее текст.
Чтобы удалить метку, надо выделить её, удерживая клавишу [Shift], и нажать клавишу [Del] или [Backspace]. При этом будут удалены все метки этой линии.
Запись и печать модели
Для записи модели (блок-схемы) на диск нужно вызвать команду Save (Сохранить) или Save As (Сохранить как) из меню File (Файл) окна модели. При этом Simulink записывает в указанную папку файл с заданным (введённым с клавиатуры) именем, присваивая ему расширение .mdl.
Чтобы распечатать модель (блок-схему), следует воспользоваться командой Print (Печать) из меню File (Файл) окна модели.
Библиотека блоков Simulink
Sources – источники сигналов
Constant – источник постоянного сигнала
Пиктограмма:
Назначение: Задает постоянный по уровню сигнал.
Окно задания параметров:
Рисунок1.1.10 – Окно задания параметров Constant
1. Constant value - Постоянная величина. Значение может быть действительным или комплексным числом, вычисляемым выражением, вектором или массивом
2. Interpret vector parameters as 1-D – Интерпретировать вектор параметров как массив скаляров
Sine Wave – источник синусоидального сигнала
Пиктограмма:
Назначение: Формирует синусоидальный сигнал с заданной частотой, амплитудой, фазой и смещением.
Для формирования выходного сигнала блоком могут использоваться два алгоритма. Вид алгоритма определяется параметром Sine Type (способ формирования сигнала):
Time-based – По текущему времени.
Sample-based – По величине шага модельного времени.
Окно задания параметров:
Рисунок 1.1.11 – Окно задания параметров Sine Wave
Формирование выходного сигнала по текущему значению времени для непрерывных систем:
Выходной сигнал источника в этом режиме соответствует выражению:
y = Amplitude* sin(frequency* time + phase) + bias.
Параметры:
Amplitude - Амплитуда.
Bias – Постоянная составляющая сигнала.
Frequency (rads/sec) - Частота (рад/с).
Phase (rads) - Начальная фаза (рад).
Sample time – Шаг модельного времени. Используется для согласования работы источника и других компонентов модели во времени. Параметр может принимать следующие значения:
· 0 (по умолчанию) – используется при моделировании непрерывных систем.
· >0 (положительное значение) – задается при моделировании дискретных систем. В этом случае шаг модельного времени можно интерпретировать как шаг квантования по времени выходного сигнала.
· -1 – шаг модельного времени устанавливается таким же, как и в предшествующем блоке, т.е. блоке, откуда приходит сигнал в данный блок.
Ramp – источник линейно изменяющегося сигнала
Пиктограмма:
Назначение: Формирует линейный сигнал вида y=Slope* time + Initial value.
Окно задания параметров:
Рисунок 1.1.12 – Окно задания параметров Ramp
· Slope — Скорость изменения выходного сигнала.
· Start time — Время начала формирования сигнала.
· Initial value — Начальный уровень сигнала на выходе блока.
Step – генератор ступенчатого сигнала
Пиктограмма:
Назначение: Формирует ступенчатый сигнал
Окно задания параметров:
Рисунок 1.1.13 – Окно задания параметров Step
· Step time - Время наступления перепада сигнала (с).
· Initial value - Начальное значение сигнала.
· Final value - Конечное значение сигнала.
Перепад может быть как в большую сторону (конечное значение больше чем начальное), так и в меньшую (конечное значение меньше чем начальное). Значения начального и конечного уровней могут быть не только положительными, но и отрицательными.
Pulse Generator – Источник импульсного сигнала
Пиктограмма:
Назначение: Формирование прямоугольных импульсов.
Окно задания параметров:
Рисунок 1.1.14 – Окно задания параметров Pulse Generator
· Pulse Type – Способ формирования сигнала. Может принимать два значения: Time-based – По текущему времени. Sample-based – По величине модельного времени и количеству расчетных шагов.
· Amplitude -Амплитуда.
· Period - Период. Задается в секундах для Time-based Pulse Type или в шагах модельного времени для Sample-based Pulse Type.
· Pulse width - Ширина импульсов. Задается в в % по отношению к периоду для Time-based Pulse Type или в шагах модельного времени для Sample-based Pulse Type.
· Phase delay - Фазовая задержка. Задается в секундах для Time-based Pulse Type или в шагах модельного времени для Sample-based Pulse Type.
· Sаmple time - Шаг модельного времени. Задается для Sample-based Pulse Type.
Clock – Источник времени
Пиктограмма:
Назначение: Формирует сигнал, величина которого на каждом шаге равна текущему значению моделирования.
Окно задания параметров:
Рисунок 1.1.15 – Окно задания параметров Clock
· Decimation - Шаг, с которым обновляются показания времени на изображении источника (в том случае, если установлен флажок параметра Display time). Параметр задается как количество шагов расчета. Например, если шаг расчета модели в окне диалога Simulation parameters установлен равным 0.01 с, а параметр Decimation блока Clock задан равным 1000, то обновление показаний времени будет производиться каждые 10 с модельного времени.
Sinks – приемники сигналов
Scope – осциллограф
Пиктограмма:
Назначение: Строит графики исследуемых сигналов в функции времени. Позволяет наблюдать за изменениями сигналов в процессе моделирования.
Для того, чтобы открыть окно просмотра сигналов необходимо выполнить двойной щелчок левой клавишей “мыши” на изображении блока. Это можно сделать на любом этапе расчета. В том случае, если на вход блока поступает векторный сигнал, то кривая для каждого элемента вектора строится отдельным цветом.
Настройка окна осциллографа выполняется с помощью панелей инструментов (рисунок 1.1.16).
Рисунок 1.1.16. Панель инструментов блока Scope
Панель инструментов содержит 11 кнопок:
1. Print – печать содержимого окна осциллографа.
2. Parameters – доступ к окну настройки параметров.
3. Zoom – увеличение масштаба по обеим осям.
4. Zoom X-axis – увеличение масштаба по горизонтальной оси.
5. Zoom Y-axis – увеличение масштаба по вертикальной оси.
6. Autoscale – автоматическая установка масштабов по обеим осям.
7. Save current axes settings – сохранение текущих настроек окна.
8. Restore saved axes settings – установка ранее сохраненных настроек окна.
9. Floating scope – перевод осциллографа в “свободный” режим.
10. Lock/Unlock axes selection – закрепить/разорвать связь между текущей координатной системой окна и отображаемым сигналом. Инструмент доступен, если включен режим Floating scope.
11. Signal selection – выбор сигналов для отображения. Опция доступна, если включен режим Floating scope.
Изменение масштабов отображаемых графиков можно выполнять несколькими способами:
1. Нажать соответствующую кнопку (
, 
или 
) и щелкнуть один раз левой клавишей “мыши” в нужном месте графика. Произойдет 2,5 кратное увеличение масштаба.
2. Нажать соответствующую кнопку (, или ) и, нажав левую клавишу “мыши”, с помощью динамической рамки или отрезка указать область графика для увеличенного изображения.
3. Щелкнуть правой клавишей “мыши” в окне графиков и, выбрать команду Axes properties … в контекстном меню. Откроется окно свойств графика, в котором с помощью параметров Y-min и Y-max можно указать предельные значения вертикальной оси. В этом же окне можно указать заголовок графика (Title), заменив выражение %< SignalLabel > в строке ввода. Окно свойств показано на рисунок 1.1.18.
Параметры:
Параметры блока устанавливаются в окне ‘Scope’ parameters, которое открывается с помощью инструмента
Рисунок 1.1.17. Увеличение масштаба графика
Рисунок 1.1.18. Окно свойств графика
(Parameters) панели инструментов. Окно параметров имеет две вкладки:
General – общие параметры.
Data history – параметры сохранения сигналов в рабочей области MATLAB.
Вкладка общих параметров показана на рисунке 1.1.19.
Рисунок 1.1.19. Вкладка общих параметров General
На вкладке General задаются следующие параметры:
1. Number of axes — число входов (систем координат) осциллографа. При изменении этого параметра на изображении блока появляются дополнительные входные порты.
2. Time range — величина временного интервала для которого отображаются графики. Если время расчета модели превышает заданное параметром Time range, то вывод графика производится порциями, при этом интервал отображения каждой порции графика равен заданному значению Time range.
3. Tick labels — вывод/скрытие осей и меток осей. Может принимать три значения (выбираются из списка):
all – подписи для всех осей,
none – отсутствие всех осей и подписей к ним,
bottom axis only – подписи горизонтальной оси только для нижнего графика.
4. Sampling — установка параметров вывода графиков в окне. Задает режим вывода расчетных точек на экран.
5. floating scope – перевод осциллографа в “свободный” режим (при установленном флажке).
На вкладке Data history (рисунок 1.1.20) задаются следующие параметры:
1. Limit data points to last – максимальное количество отображаемых расчетных точек графика. При превышении этого числа начальная часть графика обрезается. В том случае, если флажок параметра Limit data points to last не установлен, то Simulink автоматически увеличит значение этого параметра для отображения всех расчетных точек.
2. Save data to workspace – сохранение значений сигналов в рабочей области MATLAB.
3. Variable name – имя переменной для сохранения сигналов в рабочей области MATLAB.
4. Format – формат данных при сохранении в рабочей области MATLAB. Может принимать значения:
Array – массив,
Structure – структура,
Structure with time – структура с дополнительным полем “время”.
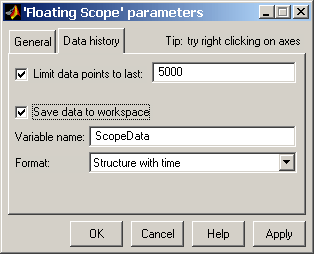
Рисунок 1.1.20. Вкладка Data history
XY Graph – графопостроитель
Пиктограмма:
Назначение: Построение графика значений одного сигнала от функции другого. Блок имеет два входа. Верхний вход предназначен для подачи сигнала, который является аргументом (X), нижний – для подачи значений функций (Y).
Окно задания параметров:
Рисунок 1.1.21 – Окно задания параметров XY Graph
· x-min – Минимальное значение сигнала по оси X.
· x-max – Максимальное значение сигнала по оси X
· y-min – Минимальное значение сигнала по оси Y.
· y-max – Максимальное значение сигнала по оси Y
· Sample time – шаг модельного времени.
Display – цифровой дисплей
Пиктограмма:
Назначение: Отображает значение сигнала в виде числа.
Окно задания параметров:
Рисунок 1.1.22 – Окно задания параметров Display
Continuous – блоки непрерывных моделей
Derivative – блок вычисления производной
Пиктограмма:
Назначение: выполняет численное дифференцирование входного сигнала.
Integrator – интегратор
Пиктограмма:
Назначение: Интегрирование входного сигнала
Окно задания параметров:
Рисунок 1.1.23 – Окно задания параметров Integrator
· Initial condition source — Источник начального значения выходного сигнала. Выбирается из списка:
internal – внутренний
external – внешний. В этом случае на изображении блока появляется дополнительный вход, обозначенный x0, на который необходимо подать сигнал задающий начальное значение выходного сигнала интегратора.
· Initial condition — Начальное условие. Установка начального значения выходного сигнала интегратора. Параметр доступен, если выбран внутренний источник начального значения выходного сигнала.
Transfer Fcn – передаточная функция
Пиктограмма:
Назначение: Блок задает передаточную функцию в виде
Окно задания параметров:
Рисунок 1.1.24 Окно задания параметров Transfer Fcn
Матричное описание числителя, векторное описание знаменателя. Размер выхода равен количеству строк числителя. Коэффициенты расположены по убыванию степени s.
· Numerator – вектор или матрица коэффициентов полинома числителя.
· Denominator – вектор коэффициентов полинома знаменателя.
· Absolute tolerance – абсолютная погрешность.
Порядок числителя не должен превышать порядка знаменателя.
Zero-Pole – передаточная функция «нули полюса»
Пиктограмма:
Назначение: Блок Zero-Pole определяет передаточную функцию с заданными полюсами и нулями:
Окно задания параметров:
Рисунок 1.1.25 – Окно задания параметров для Zero-Pole
· Zeros – Вектор или матрица нулей.
· Poles – Вектор полюсов.
· Gain – Скалярный или векторный коэффициент передаточной функции.
· Absolute tolerance — Абсолютная погрешность.
Количество нулей не должно превышать число полюсов передаточной функции.
Discrete – блоки дискретных модулей
Discrete – Time Integrator – дискретный интегратор
Пиктограмма:
Назначение: Блок используется для выполнения операций интегрирования в дискретных системах.
Окно задания параметров:
Рисунок 1.1.26 – Окно задания параметров Discrete Time Integrator
· Integration method – Метод численного интегрирования: Forward Euler (Прямой метод Эйлера), Backward Euler (Обратный метод Эйлера), Trapeziodal (Метод трапеций).
· Sample time — Шаг дискретизации по времени.
Discrete Transfer Fcn – Дискретная передаточная функция
Пиктограмма:
Назначение: Блок задает дискретную передаточную функцию в виде
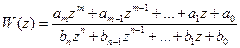
Окно задания параметров:
Рисунок 1.1.27 – Окно задания параметров Discrete Transfer Fcn
· Numerator — Вектор или матрица коэффициентов числителя
· Denominator – Вектор коэффициентов знаменателя
· Sample time — Шаг дискретизации по времени.
Порядок числителя не должен превышать порядок знаменателя.
Discrete Filter – дискретный фильтр
Пиктограмма:
Назначение: Блок задает дискретную передаточную функцию от обратного аргумента (1/z):
Окно задания параметров:
Рисунок 1.1.28 – Окно задания параметров Discrete Filter
· Numerator — Вектор или матрица коэффициентов числителя
· Denominator –Вектор коэффициентов знаменателя
· Sample time — Шаг дискретизации по времени.
Discrete Zero – Pole – дискретная передаточная функция «нули полюса»
Пиктограмма:
Назначение: Блок определяет дискретную передаточную функцию с заданными полюсами и нулями:
Окно задания параметров:
Рисунок 1.1.29 – Окно задания параметров Discrete Zero Pole
· Zeros – Вектор или матрица нулей.
· Poles – Вектор полюсов.
· Gain – Скалярный или векторный коэффициент передаточной функции.
· Sample time — Шаг дискретизации по времени.
Количество нулей не должно превышать число полюсов передаточной функции.
Discontinuities – нелинейные блоки
Relay – Реле
Пиктограмма:
Назначение: Реализует релейную нелинейность
Окно задания параметров:
Рисунок 1.1.30 – Окно задания параметров Relay
· Switch on point - Порог включения. Значение, при котором происходит включение реле.
· Switch off point - Порог выключения. Значение, при котором происходит выключение реле.
· Output when on - Величина выходного сигнала во включенном состоянии.
· Output when off - Величина выходного сигнала в выключенном состоянии.
Выходной сигнал блока может принимать два значения. Одно из них соответствует включенному состоянию реле, второе - выключенному. Переход их одного состояния в другое происходит скачком при достижении входным сигналом порога включения или выключения реле. В том случае если пороги включения и выключения реле имеют разные значения, то блок реализует релейную характеристику с гистерезисом. При этом значение порога включения должно быть больше, чем значение порога выключения.
Saturation – ограничетель
Пиктограмма:
Назначение: Выполняет ограничение величины входного сигнала.
Окно задания параметров:
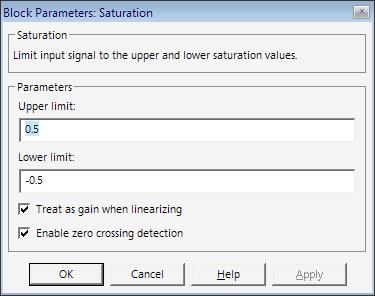
Рисунок 1.1.31 – Окно задания параметров Saturation
· Upper limit - Верхний порог ограничения.
· Lower limit - Нижний порог ограничения.
· Treat as gain when linearizing (флажок) - Трактовать как усилитель с коэффициентом передачи равным 1 при линеаризации.
Выходной сигнал блока равен входному если его величина не выходит за порог ограничения. По достижении входным сигналом уровня ограничения выходной сигнал блока перестает изменяться и остается равным порогу
Math Operation – блоки математических операций
Sum – сумматор
Пиктограмма:
Назначение: Выполняет вычисление суммы текущих значений сигналов.
Окно задания параметров:
Рисунок 1.1.32 – Окно задания параметров Sum
· Icon shape – Форма блока. Выбирается из списка: round – окружность, rectangular – прямоугольник.
· List of sign – Список знаков. В списке можно использовать следующие знаки: + ( плюс), - (минус) и | (разделитель знаков).
· Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.
Количество входов и операция (сложение или вычитание) определяется списком знаков параметра List of sign, при этом метки входов обозначаются соответствующими знаками. В параметре List of sign можно также указать число входов блока. В этом случае все входы будут суммирующими.
Если в качестве списка знаков указать цифру 1 (один вход), то блок можно использовать для определения суммы элементов вектора.
Product – блок умножения и деления
Пиктограмма:
Назначение: Выполняет вычисление произведения текущих значений сигналов.
Окно задания параметров:
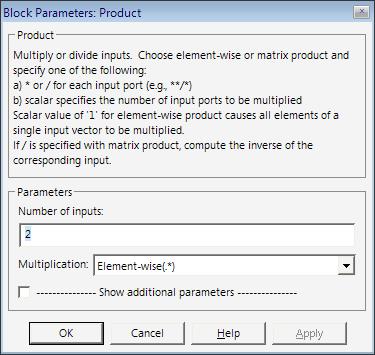
Рисунок 1.1.33 – Окно задания параметров Product
· Number of inputs – Количество входов. Может задаваться как число или как список знаков. В списке знаков можно использовать знаки * ( умножить) и / (разделить).
· Multiplication – Способ выполнения операции. Может принимать значения: Element-wise (Поэлементный), Matrix (Матричный)
· Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.
Если параметр Number of inputs задансписком, включающим кроме знаков умножения также знаки деления, то метки входов будут обозначены символами соответствующих операций.
Блок может использоваться для операций умножения или деления скалярных, векторных или матричных сигналов. Типы входных сигналов блока должны совпадать. Если в качестве количества входов указать цифру 1 (один вход), то блок можно использовать для определения произведения элементов вектора.
Gain – усилитель
Пиктограмма:
Назначение: Выполняют умножение входного сигнала на постоянный коэффициент.
Окно задания параметров:
Рисунок 1.1.34 – Окно задания параметров Gain
· Gain – Коэффициент усиления.
· Multiplication – Способ выполнения операции. Может принимать значения: Element-wise K*u (Поэлементный), Matrix K*u (Матричный), Matrix u*K (Матричный.)
· Saturate on integer overflow (флажок) - Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно
Параметр блока Gain может быть положительным или отрицательным числом, как больше, так и меньше 1. Коэффициент усиления можно задавать в виде скаляра, матрицы или вектора, а также в виде вычисляемого выражения.
Получение временных и частотных характеристик
Получение временных и частотных характеристик рассмотрим на примере колебательного звена, передаточная функция которого имеет вид:
,
Где k=1 (коэффициент усиления)
T=0.1 (постоянная времени звена)
ζ=0,3 (коэффициент относительного затухания звена)
Схема для исследования колебательного звена представлена на рисунке 1.1.35
Рисунок 1.1.35 – Схема колебательного звена
Получение переходной характеристики
Переходная характеристика h(t) представляет собой переходной процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице.
Для получения данной характеристики необходимо собрать схему, указанную на рисунок 1.1.35. Для этого необходимо:
· На панели инструментов окна браузера библиотек Simulink Library Browser щелкните по пиктограмме Создать новую модель. В окне браузера Simulink Library Browser щелкните по компоненту Continuous библиотеки simulink. Из правой части окна браузера отбуксируйте блок Transfer Fcn (Передаточная функция) в окно файла untitled.
· В левой части окна браузера Simulink Library Browser щелкните по компоненту Sources (Источники)библиотеки simulink. В правой части окна браузера появятся пиктограммы источников сигналов. Отбуксируйте блок Step в окно файла untitled. Блок Step обеспечивает формирование скачкообразного постоянного сигнала.
· В левой части окна браузера Simulink Library Browser щелкните по компоненту Sinks (Приемники) библиотеки simulink. Из правой части окна браузера отбуксируйте блок Scope (Индикатор) в окно файла untitled. Сверните все окна, кроме окна файла untitled.
· Соедините три блока, находящиеся на одном уровне для этого: Установите указатель мыши на выходе первого блока (при этом курсор должен принять форму перекрестия).Нажмите левую кнопку мыши и, удерживая ее в этом положении, передвиньте указатель ко входу второго блока. Отпустите кнопку мыши. Программа заменит указатели входов и выходов блоков соединительной линией с указанием направления передачи сигнала. Аналогично соедините второй и третий блоки.
Как только схема будет собрана, запустите процесс моделирования, щелкнув по кнопке Start simulation на панели инструментов 
. Для получения результатов моделирования дважды щелкните по изображению блоков индикаторов Scope. Переходной процесс колебательного звена изображен на рисунке 1.1.36
Рисунок 1.1.36 – Переходная характеристика колебательного звена
Еще одним способом получения характеристики h(t) является использование специального инструментального средства LTI – Viewer.
· В строке меню файла untitled выберите Tools,ав открывшемся меню команду Linear Analysis при этом откроются два окна: Окно обозревателя LTI Viewer, в котором будут строиться графики исследуемой линейной модели (При первом обращении оно пусто, по умолчанию задан режим построения графика реакции модели на скачкообразный сигнал, т.е. графика переходной функции), окно элементов, обозначающих входы и выходы исследуемой модели, Model_Inputs_and_Outputs. Элемент Input Point – предназначен для определения места подачи входного сигнала, а элемент Output Point – определяет по какой выходной координате производится исследование.
· Обозначим вход и выход блока Transfer Fcn. С этой целью последовательно отбуксируйте из окна Model_Inputs_and_Outputs в окно файла untitled элементы Input Point и Output Point. Поочередно выделите элементы в окне файла untitled и установите их так как показано на рисунке 1.1.37
Рисунок 1.1.37 Блок схема исследования колебательного звена
Для получения характеристик активизируйте окно обозревателя LTI Viewer. В строке меню выберите Simulink,ав открывшемся меню команду Get Linearized Model. В графическом поле появится график переходной функции для колебательного звена.
Съем показаний удобно производить при включенном режиме отображения сетки.
В строке меню окна обозревателя выберите Edit,ав открывшемся подменю - Viewer Preferences. В появившемся диалоговом окне откройте вкладку Style и установите галочку в поле Show Grind Дата добавления: 2017-01-21; Мы поможем в написании ваших работ!; просмотров: 629 | Нарушение авторских прав Лучшие изречения:
<== предыдущая лекция
|
следующая лекция ==>
Татищев Василий - От скифов до славян | Тема 5: Несовершенная конкуренция и рыночная власть.
| 2136 - 