Задание: Построить минимальную сокращенную ДНФ с помощью карты Карно для  .
.
Решение: В задании функции представлены в числовой форме (по наборам). Если перечисление номеров наборов предваряется знаком дизъюнкции, то на перечисленных наборах функция равна единице. Если знаком конъюнкции – нулю.
Таблица истинности заданной функции представлена в таблице 3.
Таблица 3. Таблица истинности логической функции
| Номер набора | x | y | z | f(x,y,z) |
Строим карту Карно для заданной функции. Для этого проставляем на карту значения функции (0 или 1) в соответствии с набором переменных. Например, на наборе x=1,y=0,z=1 функция равна единице. Проставляем 1 на карту в клетку  как показано на рисунке 3(а).
как показано на рисунке 3(а).
На наборе x=0,y=1,z=1 функция равна нулю. Проставляем 0 на карту в клетку  как показано на рисунке 3(б).
как показано на рисунке 3(б).
И так далее, для всех наборов. В итоге получаем карту, представленную на рисунке 3(в).
Далее необходимо сгруппировать лежащие рядом единицы в количестве степени двойки: 2, 4, 8 и т.д. Отдавать предпочтение следует наибольшим по количеству единиц группам. Единицы, уже вошедшие в группу можно объединять с другими единицами другой группы, что показано на рисунке 3 (г).
| а) | 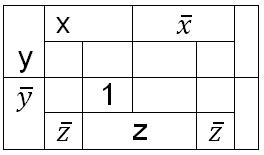
|
| б) | 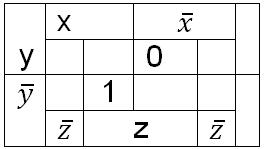
|
| в) | 
|
| г) | 
|
Рисунок 3. Карты Карно
После группировки необходимо записать в форме ДНФ «адреса» всех получившихся групп и не вошедших в группы единицы.
Карте, представленной на рисунке соответствует сокращенная ДНФ:
 .
.
Для проверки ответа необходимо построить таблицу истинности найденной сокращенной ДНФ. Если она совпадает с таблицей, которой задавалась функция f, можно писать ответ
 .
.
В третьем задании контрольной работы для студентов-заочников по дискретной математике и математической логикенужно решить комбинаторную задачу (по вариантам). Варианты третьего задания контрольной работы приведены в таблице 3.
Таблица 4. Варианты третьего задания контрольной работы
| 1. | В течение десяти недель студенты сдают 10 экзаменов, в том числе два по математике. Сколькими способами можно распределить экзамены по неделям так, чтобы экзамены по математике не следовали один за другим? |
| 2. | В приемной у зубного врача ожидают своей очереди две женщины и 10 мужчин. Для них имеется 8 экземпляров последнего номера журнала и 4 экземпляра утренней газеты. Сколькими способами могут они распределить газеты и журналы между собой, если обе женщины непременно хотят читать одно и то же? |
| 3. | Концерт состоит их трех песен и двух скрипичных пьес. Сколькими способами можно составить программу концерта так, чтобы он начинался и оканчивался исполнением песни, и чтобы скрипичные пьесы не исполнялись одна за другой? |
| 4. | Студенту необходимо сдать 4 экзамена в течение десяти дней. Сколькими способами можно составить ему расписание экзаменов? |
| 5. | Сколькими способами можно расположить в один ряд 5 красных, 4 черных и 5 белых мячей так, чтобы мячи, лежащие на краях, были одного цвета? |
| 6. | В кондитерской имеется 7 видов пирожных. Сколько всего есть способов заказать 4 пирожных? |
| 7. | Сколько имеется четырехзначных чисел, у которых каждая следующая цифра больше предыдущей? |
| 8. | Сколько существует различных четырехзначных чисел, в чьей десятичной записи могут присутствовать цифры 0, 1, 2, 3, 6, причем 0 на первом месте стоять не может? Сколько среди них четных чисел (цифру 0 считать четной)? |
| 9. | В соревнованиях по баскетболу команды A и B играют между собой несколько игр до тех пор, пока одна из команд не выиграет четыре игры. Составляется последовательность наименований команд, выигравших игры; например, последовательность ABABBB означает, что первую и третью игры выиграла команда A, остальные – команда B. Сколько таких последовательностей можно составить? |
| 10. | Группа из 41 студента успешно сдала сессию из трех экзаменов. Возможные оценки: 5, 4, 3. Доказать, что, по крайней мере, пять студентов сдали сессию с одинаковыми оценками. |






