Варианты заданий контрольной работы по дисциплине
«Дискретная математика»,
(Заочное отделение)
Номер варианта соответствует номеру студента по списку всей группы.
Теория множеств
Задание 1: Выполнить операции над множествами, представить результат графически
Множества M, А, В, С – произвольные, множество I – универсальное (универсум), Æ - пустое множество.
1) (написать ответ),
2) (заштриховать соответствующую область на диаграмме Эйлера для трех взаимно пересекающихся множеств А, В, С и записать в виде объединения конституент единицы).
Вариант 1. 1) Æ \М = (написать ответ),
2) (А\В) U(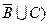
Вариант 2. 1)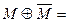 
(написать ответ),
2) 
Вариант 3. 1)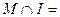 
(написать ответ),
2) 
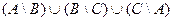
Вариант 4. 1) 
(написать ответ),
2) 
Вариант 5. 1) Æ \I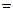 
(написать ответ),
2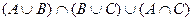 
Вариант 6. 1)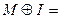 
(написать ответ),
2) 
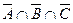
Вариант 7. 1) 
(написать ответ),
2) 
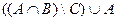
Вариант 8. 1)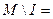 
(написать ответ),
2) 
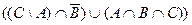
Вариант 9. 1) 
(написать ответ),
2) 
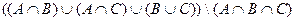
Вариант 10. 1) Æ \M=(написать ответ),
2) 
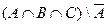
Вариант 11. 1)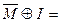 
(написать ответ),
2) 
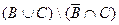
Вариант 12. 1)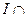 
Æ=(написать ответ),
2) 
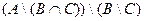
Вариант 13. 1)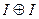 
=(написать ответ),
2) 
Вариант 14. 1)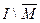 
=(написать ответ),
2) 
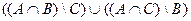
Вариант 15. 1)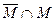 
=(написать ответ),
2) 
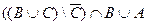
Вариант 16. 1)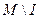 
=(написать ответ),
2) 
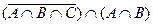
Вариант 17. 1)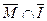 
=(написать ответ),
2)
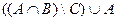
Вариант 18. 1)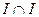 
=(написать ответ),
2) 
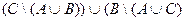
Вариант 19. 1)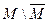 
=(написать ответ),
2) 
Вариант 20. 1)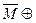 
Æ =(написать ответ),
2) 
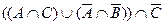
Вариант 21. 1)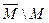 
=(написать ответ),
2) 
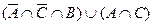
Вариант 22. 1)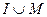 
=(написать ответ),
2) 
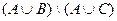
Вариант 23. 1)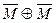 
=(написать ответ),
2) 
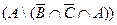
Вариант 24. 1)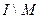 
=(написать ответ),
2) 
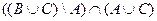
Вариант 25. 1)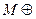 
Æ =(написать ответ),
2) 
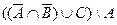
Вариант 26. 1)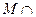 
Æ =(написать ответ),
2) 
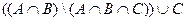
Вариант 27. 1)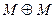 
=(написать ответ),
2) 
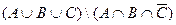
Вариант 28. 1) 
=(написать ответ),
2) 
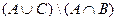
Вариант 29. 1)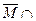 
Æ =(написать ответ),
2) 
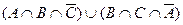
Вариант 30. 1) 
=(написать ответ),
2) 
Задание 2: По заданному десятичному числу, которое вычисляется следующим образом: 200 + номер по списку группы, заштриховать на диаграмме Эйлера для трех взаимно пересекающихся множеств А, В, С соответствующую область и записать ее в виде объединения конституент единицы.
Элементы комбинаторики.
Задание №3: Решить комбинаторные задачи.
Вариант 1.
1.Сколькими способами можно набрать очки после трех выстрелов по мишени из 10 секторов?
2.Определить число вариантов перестановок разрядов в векторе 01032.
3. Имеется три типа снаряжения. Сколькими способами можно оснастить 5 спасателей?
4. Решить комбинаторное уравнение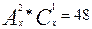 
x 
.
Вариант 2.
1.Сколькими способами можно занять места в аудитории, имеющей 15 мест, группой учащихся из 4–х человек?
2.Сколькими способами можно построить колонну из 3-х автомобилей 3-х типов? Перечислить варианты.
3. Сколькими способами можно выбрать подгруппу из 4-х учащихся из группы, состоящей из 8-ми человек?
4. Решить комбинаторное уравнение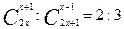 
x .
Вариант 3.
1.Сколько вариантов состояний имеет система из 9 подсистем, если каждая подсистема может находиться в 5-ти возможных состояниях?
2.Сколько комбинаций шифров можно получить перестановкой цифр в шифре 20287?
3. Сколькими способами можно выбрать пары состояний из пяти состояний системы?
4. Решить комбинаторное уравнение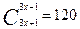 
x .
Вариант 4.
1.Сколько вариантов состояний имеет государство из четырех губерний, каждая из которых может находиться в одном из следующих состояний: а) экономический рост, б) экономический спад, г) народные волнения?
2.Сколькими способами может руководитель фирмы назначить на 5 должностей 2-х специалистов с высшим образованием? Перечислить варианты.
3. Сколько разнополых пар могут составить три юноши в обществе пяти девушек?
4. Решить комбинаторное уравнение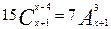 
x .
Вариант 5.
1.Сколько комбинаций двоичных коэффициентов a,b,c,d имеется для уравнения
ax-by+cz-dw=0?
2.Сколькими способами можно построить колонну из 3-х автомобилей? Перечислить варианты.
3. Сколькими способами можно составить наборы косметики из 4-х шампуней трех типов?
4. Упростить выражение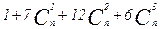 
x .
Вариант 6.
1.Сколько трехцветных флагов можно предложить из материала 4-х
цветов?
2.Сколькими способами можно расставить автомобили 10 наименований по трем стоянкам, если на первую должно быть поставлено 3, на вторую –5, а на третью –2?
3. Сколькими способами можно выбрать три квартиры из предложенных восьми?
4. Решить комбинаторное уравнение 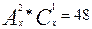x .
Вариант 7.
1.Сколько существует вариантов приобретения тремя олигархами трех разнотипных корпораций?
2.Сколькими способами можно составить слова из символов &, *, ^, $?
3. Сколькими способами можно выбрать два особняка в престижном районе Лондона из предлагаемых пяти?
4. Решить комбинаторное уравнение 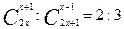x .
Вариант 8.
1.Сколькими способами пять семей приобретут по одной квартире в восьми квартирном доме?
2.Сколькими способами можно переставить три строки и два столбца некоторой матрицы?
3. Сколько можно выбрать подгрупп из четырех специалистов, если в группе специалистов 7 человек?
4. Решить комбинаторное уравнение 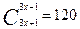x .
Вариант 9.
1.Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 5 команд трех типов?
2.Сколькими способами можно переставить буквы в слове «перешеек»?
3. Сколько можно составить бригад из 5 инженеров 4-х специальностей?
4. Решить комбинаторное уравнение 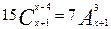x .
Вариант 10.
1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 4 команд трех типов?
2. Подсчитайте число последовательностей, получаемых перестановками символов в последовательности 0132?
3.Сколько пар можно выбрать из 5 студентов?
4. Упростить выражение 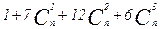x .
Вариант 11.
1.Сколько десятичных трехзначных чисел существует?
2.Определить число вариантов перестановок символов в слове авасд.
3. Имеется три типа обуви. Сколькими способами можно обуть 5 экстремалов?
4. Решить комбинаторное уравнение 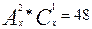x .
Вариант 12.
1.Сколькими способами можно занять места на соревнованиях, в которых участвуют 15 спортсменов, командой из 4 –х человек, если никакие два участника не набирают одинакового количества очков?
2.Сколькими способами можно построить колонну из 3-х кораблей 3-х типов? Перечислить варианты.
3. Сколькими способами можно выбрать подгруппу из 4-х учителей из группы, состоящей из 8-учителей?
4. Решить комбинаторное уравнение 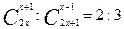x .
Вариант 13.
1.Сколько вариантов состояний имеет устройство из 9 микросхем, если каждая микросхема может находиться в 5-ти возможных состояниях?
2.Сколько комбинаций шифров можно получить перестановкой цифр в шифре 80827?
3. Сколькими способами можно выбрать пары состояний из пяти состояний устройства?
4. Решить комбинаторное уравнение 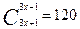x .
Вариант 14.
1.Сколько вариантов состояний имеет государство из четырех республик, каждая из которых может находиться в одном из следующих состояний: а) экономический спад, б) стабильность, г) революция?
2.Сколькими способами может руководитель департамента назначить на 5 должностей 2-х специалистов с высшим образованием? Перечислить варианты.
3. Сколько разнополых пар могут составить три девушки в обществе пяти юношей?
4. Решить комбинаторное уравнение 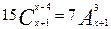x .
Вариант 15.
1.Сколько комбинаций двоичных коэффициентов a,b,c,d имеется для уравнения
ax-by+cz-dw=0?
2.Сколькими способами можно построить колонну из 3-х мотоциклов? Перечислить варианты.
3. Сколькими способами можно составить наборы продуктов из 4-х продуктов трех типов?
4. Упростить выражение 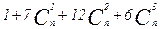x .
Вариант 16.
1.Сколько трехцветных футболок можно сшить из материала 4-х
цветов?
2.Сколькими способами можно расставить автомашины 10 наименований по трем стоянкам, если на первую должно быть поставлено 3, на вторую –5, а на третью –2?
3. Сколькими способами можно выбрать три квартиры из предложенных восьми?
4. Решить комбинаторное уравнение 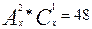x .
Вариант 17.
1.Сколько существует вариантов приобретения тремя олигархами трех разнотипных комбинатов?
2.Сколькими способами можно составить слова из символов &, *, ^, $?
3. Сколькими способами можно выбрать два особняка в престижном районе Лондона из предлагаемых пяти?
4. Решить комбинаторное уравнение 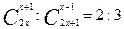x .
Вариант 18.
1.Сколькими способами пять семей приобретут по одной квартире в восьми квартирном доме?
2.Сколькими способами можно переставить три столбца и две строки некоторой матрицы?
3. Сколько можно выбрать подгрупп из четырех специалистов, если в группе специалистов 7 человек?
4. Решить комбинаторное уравнение 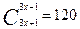x .
Вариант19.
1.Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 5 команд трех типов?
2.Сколькими способами можно переставить буквы в слове «Веремеев»?
3. Сколько можно составить бригад из 5 -ти рабочих 4-х специальностей?
4. Решить комбинаторное уравнение 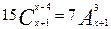x .
Вариант 20.
1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 4 команд трех типов?
2. Подсчитайте число последовательностей, получаемых перестановками символов в последовательности 0132?
3.Сколько пар можно выбрать из 5 школьников?
4. Упростить выражение 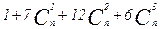x .
Вариант 21.
1.Сколькими способами можно набрать очки после трех выстрелов по мишени из 9 секторов?
2.Определить число вариантов перестановок разрядов в векторе 010323.
3. Имеется три типа снаряжения. Сколькими способами можно оснастить 4 спасателей?
4. Решить комбинаторное уравнение 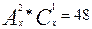x .
Вариант 22.
1.Сколькими способами можно занять места в аудитории, имеющей 10 мест, группой учащихся из 4 –х человек?
2.Сколькими способами можно построить колонну из 4-х автомобилей 4-х типов? Перечислить варианты.
3. Сколькими способами можно выбрать подгруппу из 4-х учащихся из группы, состоящей из 9-ми человек?
4. Решить комбинаторное уравнение 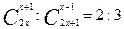x .
Вариант 23.
1.Сколько вариантов состояний имеет система из 8 подсистем, если каждая подсистема может находиться в 5-ти возможных состояниях?
2.Сколько комбинаций шифров можно получить перестановкой цифр в шифре 202870?
3. Сколькими способами можно выбрать пары состояний из пяти состояний системы?
4. Решить комбинаторное уравнение 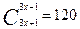x .
Вариант 24.
1.Сколько вариантов состояний имеет государство из трёх губерний, каждая из которых может находиться в одном из следующих состояний: а) экономический рост, б) экономический спад, г) народные волнения?
2.Сколькими способами может руководитель фирмы назначить на 4 должностей 2-х специалистов с высшим образованием? Перечислить варианты.
3. Сколько разнополых пар могут составить три юноши в обществе пяти девушек?
4. Решить комбинаторное уравнение 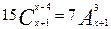x .
Вариант 25.
1.Сколько комбинаций двоичных коэффициентов a,b,c,d имеется для уравнения
ax-by+cz-dw=0?
2.Сколькими способами можно построить колонну из 3-х автомобилей? Перечислить варианты.
3. Сколькими способами можно составить наборы косметики из 3-х шампуней трех типов?
4. Упростить выражение 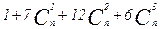x .
Вариант 26.
1.Сколько трехцветных флагов можно предложить из материала 3-х
цветов?
2.Сколькими способами можно расставить автомобили 10 наименований по трем стоянкам, если на первую должно быть поставлено 3, на вторую –5, а на третью –2?
3. Сколькими способами можно выбрать три квартиры из предложенных восьми?
4. Решить комбинаторное уравнение 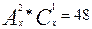x .
Вариант 27.
1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 5 команд трех типов?
2. Подсчитайте число последовательностей, получаемых перестановками символов в последовательности 013270?
3.Сколько пар можно выбрать из 8 школьников?
4. Упростить выражение 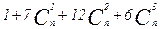x .
Вариант 28.
1.Сколькими способами пять семей приобретут по одной квартире в восьми квартирном доме?
2.Сколькими способами можно переставить три столбца и две строки некоторой матрицы?
3. Сколько можно выбрать подгрупп из четырех специалистов, если в группе специалистов 7 человек?
4. Решить комбинаторное уравнение 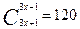x .
Вариант 29.
1.Сколько комбинаций двоичных коэффициентов a,b,c,d имеется для уравнения
ax-by+cz-dw=0?
2.Сколькими способами можно построить колонну из 3-х мотоциклов? Перечислить варианты.
3. Сколькими способами можно составить наборы продуктов из 4-х продуктов трех типов?
4. Упростить выражение 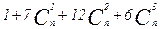x .
Вариант 30.
1. Подсчитайте число программ, не обязательно имеющих смысл, состоящих из 4 команд трех типов?
2. Подсчитайте число последовательностей, получаемых перестановками символов в последовательности 0132?
3.Сколько пар можно выбрать из 5 студентов?
4. Упростить выражение 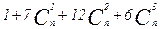x .
Элементы теории графов.
Задание №4: Задан неориентированный граф без петель из пяти вершин строками полуматрицы смежности в виде шестнадцатеричного числа, где первая цифра- первая строка полуматрицы, вторая цифра – вторая строка и т.д. Изобразить по заданному шестнадцатеричному числу граф в виде рисунка и определить степени всех вершин, цикломатическое и хроматическое число. Изобразить ориентированный граф из четырёх вершин по тому же числу, но полагать, что каждая цифра – строка матрицы смежности орграфа.
Вариант 1). 9221
Вариант 2). А321
Вариант 3). В331
Вариант 4). С421
Вариант 5). Д431
Вариант 6). 9221
Вариант 7). F531
Вариант 8). E631
Вариант 9). D521
Вариант 10). C431
Вариант 11). B321
Вариант 12). F721
Вариант 13). 9431
Вариант 14). F321
Вариант 15). E231
Вариант 16). D431
Вариант 17). C521
Вариант 18). B731
Вариант 19). A731
Вариант 20). 9531
Вариант 21). F221
Вариант 22). C721
Вариант 23). B531
Вариант 24). A621
Вариант 25). D231
Вариант 26). 9220
Вариант 27). A701
Вариант 28). B321
Вариант 29). F721
Вариант 30). 9431
Основы теории переключательных функций
Задание 5: Переключательная функция от трех аргументов задана номером в десятичной системе счисления. Получить номер ПФ в двоичном, восьмеричном и шестнадцатеричном кодах, таблицу истинности, определить СДНФ, СКНФ, символическую форму функции с восьмеричной нумерацией наборов. Минимизировать функцию по кубу соседних чисел и карте Карно. Определить свойства функции. Реализовать функцию переключательной схемой на функциональных элементах в базисах а) И, ИЛИ, НЕ, б) И-НЕ, в) ИЛИ-НЕ.
Варианты заданий соответствуют номеру по списку группы
.
| 1) | ПФ №241 |
| 2) | ПФ №165 |
| 3) | ПФ №55 |
| 4) | ПФ №143 |
| 5) | ПФ №7 |
| 6) | ПФ №29 |
| 7) | ПФ №183 |
| 8) | ПФ №248 |
| 9) | ПФ №234 |
| 10) | ПФ №77 |
| 11) | ПФ №253 |
| 12). | ПФ №249 |
| 13) | ПФ №71 |
| 14) | ПФ №224 |
| 15) | ПФ №229 |
| 16) | ПФ №90 |
| 17) | ПФ №88 |
| 18) | ПФ №133 |
| 19) | ПФ №247 |
| 20) | ПФ №161 |
| 21) | ПФ №244 |
| 22) | ПФ №150 |
| 23) | ПФ №181 |
| 24) | ПФ №39 |
| 25) | ПФ №157 |
| 26) | ПФ №251 |
| 27) | ПФ №79 |
| 28) | ПФ №67 |
| 29) | ПФ №105 |
| 30) | ПФ №142 |
Контрольная работа выполняется от руки в отдельной ученической тетради в клеточку, на обложку наклеивается распечатанный титульный лист.
Срок сдачи – за 30 дней до начала экзаменационной сессии.
Министерство сельского хозяйства РФ,
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермская Государственная сельскохозяйственная академия имени академика Д.Н.Прянишникова»
Кафедра информационных технологий
