Материальной точки без учета сопротивления среды.

Расчетная РАБОТА

 

по дисциплине

«Теоретическая механика»

 

ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ»

(вариант 9)

 

Руководитель,

ассистент __________________ (Б. Р. Хакимов)

^{(подпись с указанием даты подписания)}

 

 

Исполнитель,

студент группы 2211-81 ___________________ (В. А. Каюмова)

^{(подпись с указанием даты подписания)}

 

Казань 2012

ИСХОДНЫЕ ДАННЫЕ

Схема трубки ABCD, в которой движется материальная точка M, приведена на рисунке 1. Значения исходных данных приведены в таблице 1.

	D

 

M

M

A

15o

75º

B

 

Рисунок 1 - Схема изогнутой трубки ABCD

 

 

Таблица 1- Исходные данные

Данные	m	VA	P	τ	l	VD	f	Q	R
кг	м/с	Н	с	м	м/с	Н	Н
Значения				1,5			0,32	5∙ t2	0,2∙ V2

 

РЕШЕНИЕ

Часть 1. Интегрирование дифференциального уравнения движения

материальной точки без учета сопротивления среды.

Каждый участок движения материальной точки рассмотрим отдельно и для него составим и решим дифференциальное уравнение (далее ДУ) движения точки.

1. Рассмотрим участок AB. Схема участка с действующими на материальную точку силами приведена на рисунке 2.

 

		V
	N

A

M

B

x

G

 

Рисунок 2 – Схема участка AB

 

На данном участке на материальную точку кроме силы тяжести действует сила Q и нормальная реакция опоры N. Запишем ДУ движения материальной точки М на участке АВ в проекции на ось x:

 

Решим уравнения путем разделения переменных:

 

Константу интегрирования С₁ определим исходя из начальных условия. При t = 0, V = V_A, тогда:

 

Полученное уравнение (10) позволяет определить скорость точки в любой момент времени на участке движения АВ. В момент времени при t = τ скорость точки V = V_B.

 

 

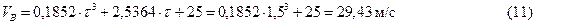
2. Рассмотрим участок BС. Схема участка с действующими на материальную точку силами приведена на рисунке 3.

y

N

Fтр

P

B

C

x

 

G

 

 

Рисунок 3 - Схема участка BC

 

На данном участке на материальную точку кроме силы тяжести действует постоянная сила P. Запишем ДУ движения материальной точки М на участке ВС в проекции на ось x:

 

 

При движение сила трения равна:

 

Нормальную реакцию опоры определим, составим уравнение движения в проекцию на ось у. Так как движение в направлении этой оси отсутствует, то сумма всех сил в проекции на эту ось равна нулю:

 

Подставим полученное в уравнении (17) значение нормальной реакции опоры в уравнение (14) получим:

 

 

Подставим в уравнение (13) получим:

 

 

Решим уравнение путем разделения переменных:

 

Константу интегрирования С ₁ определим исходя из начальных условий. При t = 0 (отчет времени на участке ВС ведем заново), V = V_B, тогда:

 

 

 

Полученное уравнение (27) позволяет определить скорость точки в любой момент времени на участке движения ВC. В исходных данных дана длинна участка ВС, и для определения времени движения на данном участке необходимо установить зависимость пройденного пути от времени (закон движения). Закон устанавливается путем интегрирования уравнения скорости точки:

 

 

Константу интегрирования С₂ определим исходя из начальных условий. При t=0, x=0 (точу B принимаем за точку начала отсчета), тогда:

 

Полученное уравнение (33) – закон движения материальной точки М на участке ВС. В момент времени при t=T, перемещение x=l:

 

 

 

 

Материальная точка М достигает точки С через 0,52 с движения на участке ВС. Очевидно, что для дальнейшего решения необходимо использоваь значение T₁ . Подставим полученное значение времени T в уравнение (27) получим значение скорости материальной точки М в точке С:

 

 

 

3. Рассмотрим участок СD. Схема участка с действующими на материальную точку силами приведена на рисунке 4.

N

y

M

V

	Fтр		G

75º

C

Рисунок 4- Схема участка CD

 

На данном участке на материальную точку кроме силы тяжести действует постоянная сила трения F_тр и нормальная реакция опоры N. Запишем ДУ движения материальной точки М на участке CD в проекции на ось x:

 

Нормальную реакцию опоры определим, составив уравнение движения в проекции на ось y. Так как движение в направлении этой оси отсутствует, то сумма всех сил в проекции на эту ось равна нулю:

 

Подставив полученное уравнение (44) в уравнение (41), получим:

 

 

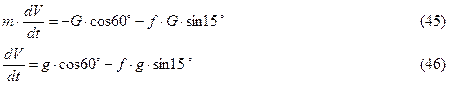
Решим уравнение путём разделения переменных:

 

 

Константу интегрирования С ₁ определим исходя из начальных условия. При t = 0 (отчет времени на участке СD ведем заново), V = V _C, тогда:

 

 

Полученное уравнение (52) позволяет определить скорость точки в любой момент времени на участке движения CD. Определим время движения t ₁ на участке CD по условию, что в момент времени t = t ₁ скорость материальной точки V = V _D =0: