Особенности геометрии и условий работы косозубых зубчатых передач

Зубья косозубых цилиндрических колес нарезают тем же инст­рументом, что и прямозубых. Ось червячной фрезы составляет с торцовой плоскостью колеса угол β (рис. 15.5). При нарезании фрезу перемещают по направлению зубьев колеса. Поэтому в нормальной к направлению зуба плоскости все его размеры - стандартные.

У пары сопряженных косозубых колес с внешним зацеплением углы β наклона линий зубьев равны, но противоположны по направ-

 

лению. Если не предъяв­ляют специальных требо­ваний, то колеса нареза­ют с правым направлени­ем зуба, а шестерни - с левым.

Рис. 15.5

У косозубого колеса (рис. 15.5) расстояние между зубьями можно измерить в торцовом, или окружном, (t - t) и нор­мальном (п - п) направле­ниях. В первом случае получают окружной шаг р _tво втором - нор­мальный шаг p. Различны в этих направлениях и модули зацепления: ; ,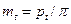

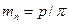где m_t и m_n - окружной и нормальный модули зубьев. Согласно рис. 15.5,

следовательно,

где β - угол наклона зуба на делительном цилиндре.

Нормальный модуль должен соответствовать стандарту.

В торцовой плоскости t - t косозубое колесо можно рассматривать как прямозубое с модулем m_t и углом зацепления α_t: tg α_t = tgα/cosβ.

Для колеса без смешения делительный d и начальный d_w диа­метры

d=d_w = m _t z = m_nz/cosβ.

Помимо торцового перекрытия в косозубых передачах обеспе­чено и осевое перекрытие. Коэффициент осевого перекрытия

где р_x - осевой шаг, равный расстоянию между одноименными точ­ками двух смежных зубьев, измеренному в направлении оси зубча­того колеса (рис. 15.5).

 

Особенности геометрии опреде­ляют отличия условий работы косозубой передачи.

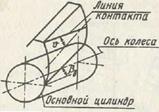
Рис. 15.6

1. Линии контакта на косозубом колесе расположены параллельно оси вращения (рис. 15.6) под углом к полюсной линии (на прямозубом колесе параллельно полюсной линии). Здесь β_b-угол наклона зуба на основном цилиндре. Зуб ведомого

колеса входит в зацепление, начиная с вершины, вначале увеличи­вая, а затем уменьшая длину контактной линии при перемещении ее от головки зуба к ножке. Вследствие того, что зуб работает не сразу всей длиной, он лучше и быстрее прирабатывается.

2. В отличие от прямозубой в косозубой передаче зубья входят
в зацепление не сразу по всей длине, а постепенно. Увеличивается
время контакта одной пары зубьев, в течение которого входят в за-­
цепление новые пары зубьев; нагрузку передает большее число кон­-
тактных линий, что значительно снижает шум и динамические на­-
грузки. Чем больше угол β наклона линии зуба (рис. 15.5), тем выше
плавность зацепления.

3. Нагрузка по длине контактной линии распределяется про­-
порционально суммарной жесткости зубьев шестерни и колеса (рис.
15.7, а). На рис. 15.7, б показан контакт сопряженных зубьев в ха­-
рактерных сечениях и их схематизированное изображение при опре­
делении суммарной жесткости. При контакте одним из сопряженных
зубьев в вершине (сечения I и III) жесткость меньше и нагрузка
меньше. Такое распределение нагрузки положительно сказывается
на работе передачи.

4. В косозубой передаче в зацеплении участвуют одновремен­но 2-3 пары зубьев. Поэтому суммарная длина l _∑koc контактных ли­ний больше (примерно на 30 %), чем в прямозубой передаче l _∑прям:

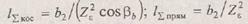
При этом значения коэффициента Z_ε, учитывающего суммар­ную длину контактных линий:

для косозубых передач ;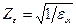

для прямозубых передач ,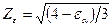

где ε_α - коэффициент торцового перекрытия.

5. Соотношение между радиусами кривизны контактирующих зубьев в косозубой передаче более благоприятно:

Это находит отражение при вычислении коэффициента Z_H, учи-тывающего форму сопряженных поверхностей зубьев.

Контактные напряжения при прочих равных условиях в косозу-бом зацеплении меньше по значению, чем в прямозубом.