Расчет прямозубых цилиндрических передач на контактную прочность

Контактная прочность зубьев является основным критерием работоспособности большинства зубчатых передач. При выводе расчетной зависимости по условию контактной прочности рассмат­ривают контакт зубьев в полюсе W, в зоне однопарного зацепления, где и наблюдают выкрашивание (рис. 15.2). На рис. 15.2 обозначе­ны: О₁О₂ = a_w — межосевое расстояние; N₁N₂ - линия зацепления (ка-

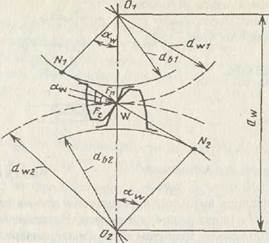
Рис. 15.2

сательная к основным окружностям); a_w - угол зацепления; d_b1 и d_b2 -диаметры основных окружностей; d_w1 и d_w2 - диаметры начальных ок­ружностей. В передачах без смещения делительные и начальные ок­ружности зубчатых колес совпадают: d=d_w. Ранее (см. раздел 14.1) было получено:

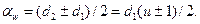Откуда

d_l = 2a_w/(u ±1) и d₂ = 2a_wu/(u ± l),

где u = d₂/d₁ - передаточное число передачи.

Наибольшее контактное напряжение в зоне зацепления опреде­ляют по формуле Герца, полученной для контакта двух цилиндров с параллельными осями (рис. 13.6):

Силу F_n, действующую по нормали к профилям (по линии заце­пления в точке контакта), определяют по окружной силе F, с учетом коэффициента нагрузки К_H.

F_n = K_HF_t /cos a_w.

Длина l_∑ контактных линий в процессе зацепления зубчатых ко­лес с прямыми зубьями меняется от рабочей ширины b₂ венца колеса в зоне однопарного зацепления до 2b₂ в зоне двухпарного зацепле­ния. Угол поворота зубчатого колеса при перемещении точки каса­ния профилей из одного крайнего положения в другое называют уг­лом торцового перекрытия. Отношение угла торцового перекрытия к угловому шагу 2π/z называют коэффициентом ε_α торцового пере­крытия. Здесь z - число зубьев зубчатого колеса.

По результатам экспериментов для расчетов суммарную длину b = l_∑ контактных линий определяют с учетом коэффициента торцо­вого перекрытия ε_α:

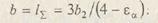
Контакт зубьев рассматривают как контакт двух цилиндров с радиусами, равными радиусам кривизны профилей зубьев в полюсе зацепления: ρ₁ = N₁W и ρ₂ = N₂W. Тогда

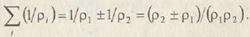
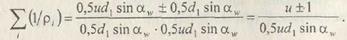
Подставим полученные зависимости в формулу Герца:

Из прямоугольного треугольника O₁N₁W имеем: ρ₁ = N₁W = 0,5 d₁ sinα_w; из треугольника O₂N₂W: ρ₂ = N₂W = 0,5 d₂ sinα_w = 0,5u d₁ sinα_w. Тогда

 

 

 

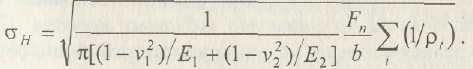
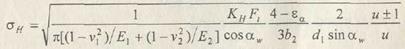
Для вывода расчетной зависимости выразим входящие в фор­мулу Герца величины через параметры зацепления.

Обозначим

 

 

- коэффициент, учитываю-

щий упругие свойства материалов сопряженных колес: Z_E = 191,6 МПа^0,5 для стальных колес при Е₁= Е₂ = 2,5.10⁵ МПа и ν₁= ν₂ = 0,3;

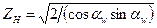- коэффициент, учитывающий форму

сопряженных поверхностей зубьев в полюсе зацепления; Z_H = 2,5 при α_w = 20 °;

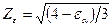- коэффициент, учитывающий суммарную длину контактных линий; Z_ε = 0,9 для прямозубых колес при ε_α = 1,6.

При этом получим расчетную зависимость в форме, рекомендо­ванной стандартом:

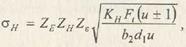
(15.1)

где и –передаточное число; F_t в Н; d₁ и b₂ в мм; σ_H в МПа.

Заменив в этой формуле F_t = 2. 10³ T₁ / d₁ и выразив b₂ и d₁ че­рез a_w: b₂ = ψ_baa_w и d₁ = 2 a_w /(u ± l), последовательно получим

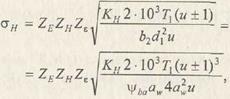
здесь T₁ - вращающий момент на шестерне, Нм.

Запишем теперь условие прочности σ_H ≤ [σ] _H в виде

Решив относительно aw, получим

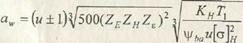
Обозначим

(15.2)

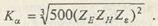
Окончательно формула проектировочного расчета цилинд­рических зубчатых передач имеет вид:

(15.3)

где a_w - межосевое расстояние, мм; К_H - коэффициент нагрузки; Т₁ -вращающий момент на шестерне, Н м; [σ] _H - допускаемое контакт­ное напряжение, МПа.

В соответствии со стандартом:

для прямозубых передач К_а = 450 МПа^1/3;

для косозубых и шевронных передач К_а = 410 МПа^1/3.

В целом межосевое расстояние косозубой цилиндрической зуб­чатой передачи примерно на 20 % меньше межосевого расстояния прямозубой передачи.

При расчете цилиндрических передач значение коэффициента ширины зубчатого венца колеса ψ_ba =b₂/a_w задают. В зависимо­сти от расположения шестерни относительно опор принимают: ψ_ba =0,2…0,5.

Формулу для проверочного расчета получим на основе форму­лы (15.2):

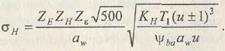
Обозначив 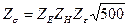и заменив ψ_baa_w = b₂, получим формулу для проверочного расчета цилиндрических зубчатых передач:

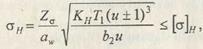
где T₁ - в Нм; a_w и b₂ - в мм; σ_H - в МПа.

Значения коэффициента Z_σ для цилиндрических стальных передач: прямозубых Z_σ = 9600 МПа^1/2; косозубых и шевронных Z_σ = 8400 МПа^1/2.

При проектировочном расчете значение коэффициента расчет­ной нагрузки задают ориентировочно: К_H = 1,3. При проверочном расчете определяют его уточненное значение по известным разме­рам и степени точности передачи.

При выполнении проверочного расчета желательно достижение равенства σ_H = [σ] _H, так как при σ_H > [σ] _H, возможно занижение ре­сурса передачи, а при σ_H < [σ] _H завышение ее массы. Простейшим способом достижения σ_H = [σ] _H является изменение ширины зубча­того венца b_2. Из полученных формул следует, что контактная прочность зубьев колес зависит от материала и размеров передачи и не зависит от модуля и числа зубьев в отдельности. По условиям контактной прочности при данном a_w модуль и числа зубьев могут иметь различ­ные значения, но с соблюдением условий: 0,5m( z_1` + z₂) = a_w и .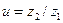

Контрольные вопросы

1. Каков физический смысл коэффициентов К_H и K_F нагрузки при
расчете зубчатых передач на контактную и изгибную прочность?

2. От чего зависит коэффициент К_Hβ неравномерности распре­-
деления нагрузки по длине контактных линий? Каким образом мож­-
но уменьшить его значения?

3. От чего зависит коэффициент К_HV внутренней динамики на­-
гружения? Каким образом можно уменьшить его значения?

4. От чего зависит коэффициент К_Hα распределения нагрузки
между зубьями? Каким образом можно уменьшить его значения?

5. Как из формулы Герца выводят формулу для расчета рабо­-
чих поверхностей зубьев на контактную прочность? Что учитывают
коэффициенты Z_E, Z_h и Z_ε вполученной формуле?

6. От каких параметров прямозубой передачи зависят контакт-­
ные напряжения? Как можно уменьшить значение контактных на-­
пряжений?

7. Какой основной параметр зубчатой цилиндрической переда­-
чи определяют при расчете?

8. Как влияет на размеры передачи величина коэффициента ψ_ba
ширины венца?

9. Изменение каких параметров зубчатых колес влияет на кон­-
тактную прочность?

ЛЕКЦИЯ 17

TEMAJ5