Графический метод кинематического анализа

Степень подвижности пространственного мезанизма.Формула

Что бы из кинематической цепи получить механизм необходимо:

одно звено сделать неподвижным,образовать станину,,одному или нескольким звеньям задать закон движение(сделать ведущими)таким образом что бы остальные звенья совершали требуемые целесообразные движения.

Знать обобщеную координату механизма(каждая из независимых координат определяющих положение всех звеньев относительно неподвижного звена(стойки))и число степеней свободы механизма(число степеней свободы всей кинематической цепи относительно неподвижного звена(стойки)

Для пространственной кинематической цепи n-кол-во подвижных звеньев,количество степеней свободы всех звеньев-6n,количество кинематических пар 5-го класса-P5,количество связей наложеных кинематическими парама 5-го класса на звенья входящие в них-5P5

Количество кинематических пар 4-го класса-P4

количество связей наложеных кинематическими парами 4-го класса на звенья входящие в них-4P4 и тд

Звенья кинематической цепи образуя кинематические пары с другими звеньями утрачивают часть степеней свободы,оставшиеся число степеней свободы кинематической цепи относительно стойки можно вычислить по формуле:

W=6n-5P5-4P4-3P3-2P2-1P1-это структурная формула пространственной цепи(формула Малышева) Величину(W)-наз. степенью подвижности механизма(если из кинем.цепи образован механизм).

Степень подвижности плоского механизма.Формула

Что бы из кинематической цепи получить механизм необходимо:

одно звено сделать неподвижным,образовать станину,,одному или нескольким звеньям задать закон движение(сделать ведущими)таким образом что бы остальные звенья совершали требуемые целесообразные движения.

Знать обобщеную координату механизма(каждая из независимых координат определяющих положение всех звеньев относительно неподвижного звена(стойки))и число степеней свободы механизма(число степеней свободы всей кинематической цепи относительно неподвижного звена(стойки).

Для плоской кинематической цепи и соответственно для плоского механизма W= 3n-2P5-P4 -формула Чебышева.

 

 

Использование методов засечек в кинематическом анализе

Графический метод кинематического анализа(метод засечек типо)

 

Преимущество этого метода заключается в наглядности и простоте. Он хорош для кинематического анализа звеньев, совершающих возвратно-поступательное движение. Недостаток метода – невысокая точность, которая зависит от точности графических построений.

Задача о положениях решается построением нескольких совмещённых планов механизма в выбранном масштабе длин при различных последовательных положениях ведущего звена.

Задачи о скоростях и ускорениях решаются построением графиков (диаграмм) перемещений, скоростей и ускорений исследуемой точки.

Последовательность кинематического анализа:

1. Сначала строят несколько (чаще всего 12 и более) совмёщенных планов механизма в произвольно выбранном масштабе длин.

2. Затем строят график пути (перемещения) исследуемой точки или звена, для чего используют совмещённые планы механизма и последовательные положения на них исследуемой точки или звена.

3. Графическим дифференцированием графика перемещений строят график скорости исследуемой точки.

4. Графическим дифференцированием графика скоростей строят график ускорений.

Графическое дифференцирование можно производить методом хорд и методом касательных. С целью повышения точности удобно использовать оба метода одновременно.

Метод планов в кинематичском анализе

Графоаналитический метод

Графоаналитический метод называют методом планов скоростей и ускорений.

Задача о положениях решается графическим методом, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин.

Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма.

Преимущество этого метода по сравнению с графическим в том, что он менее трудоёмок, так как позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.

Недостатком метода является то, что требуется построить планы скоростей и ускорений для нескольких положений механизма (если необходимо определять скорость и ускорение при различных положениях механизма и его звеньев).

Следует помнить, что в основе построения планов скоростей и ускорений лежат законы плоскопараллельного движения. Согласно этим законам:

1. План скоростей (а также план ускорений) получается в результате графического решения векторных уравнений для определения скоростей (ускорений) точек в плоскопараллельном движении;

2. Векторы абсолютных скоростей точек (при рассмотрении их движения относительно неподвижного звена) изображаются исходящими из полюса плана, а направление совпадает с касательными к траектории движения. Векторы относительных скоростей точек (при их движении относительно подвижных точек) изображаются отрезками, соединяющими концы соответствующих векторов абсолютных скоростей;

3. Длина векторов относительных скоростей пропорциональна длине тех участков звеньев, которые являются радиусами вращения точек в их относительном движении. Это положение, известное под названием теоремы подобия, облегчает определение скоростей многих точек, лежащих на звеньях плоскопараллельного и вращательного движения.

20. Методы планов в кинематическом анализе.Пример(http://www.prikladmeh.ru/lect32.htm)там много, не знаю точно что все брать..

 

Методы:

- графический (или метод графиков и диаграмм);

- графоаналитический (или метод планов скоростей и ускорений);

- аналитический;

- экспериментальный.

Графический метод кинематического анализа

Преимущество этого метода заключается в наглядности и простоте. Он хорош для кинематического анализа звеньев, совершающих возвратно-поступательное движение. Недостаток метода – невысокая точность, которая зависит от точности графических построений.

Задача о положениях решается построением нескольких совмещённых планов механизма в выбранном масштабе длин при различных последовательных положениях ведущего звена.

Задачи о скоростях и ускорениях решаются построением графиков (диаграмм) перемещений, скоростей и ускорений исследуемой точки.

Последовательность кинематического анализа:

1. Сначала строят несколько (чаще всего 12 и более) совмёщенных планов механизма в произвольно выбранном масштабе длин.

2. Затем строят график пути (перемещения) исследуемой точки или звена, для чего используют совмещённые планы механизма и последовательные положения на них исследуемой точки или звена.

3. Графическим дифференцированием графика перемещений строят график скорости исследуемой точки.

4. Графическим дифференцированием графика скоростей строят график ускорений.

Графическое дифференцирование можно производить методом хорд и методом касательных. С целью повышения точности удобно использовать оба метода одновременно.

 

Пример 1.

Даны кривошипно-ползунный механизм, длины звеньев которого – кривошипа и шатуна – L_OA и L_AB соответственно, и угловая скорость кривошипа .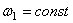

Определитьскорости и ускорения ползуна при различных положениях кривошипа.

Решение.

Выбираем масштабы длин 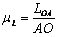, м/мм, где AO – длина отрезка, мм, изображающая кривошип длиной L_ОА на строящемся плане механизма; эта длина выбирается произвольно с учётом того, что совмещённые планы механизма должны разместиться на отведённом месте чертежа, а сам масштаб длин был бы удобен для дальнейших расчётов.

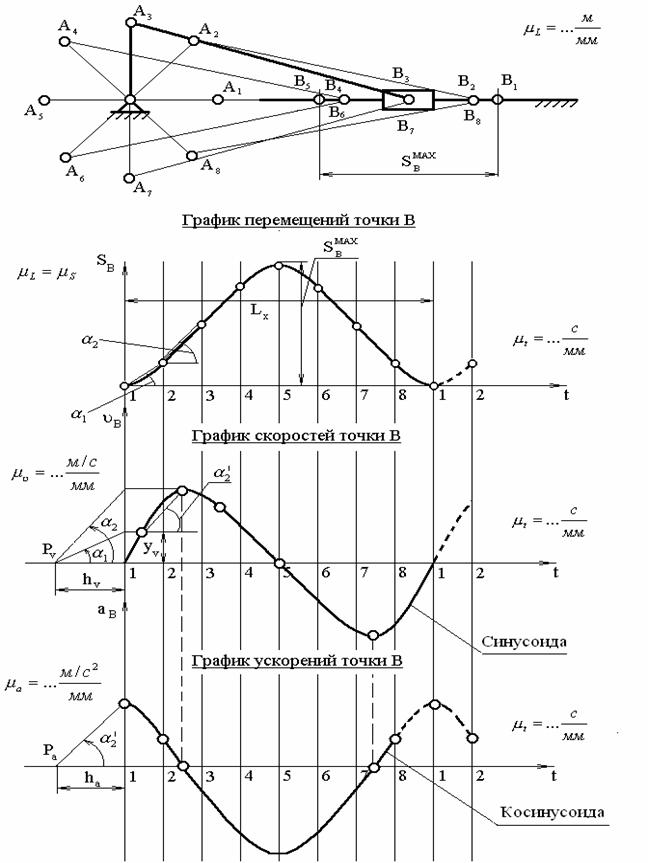
Вычисляем длину отрезка , мм, изображающего шатун на плане механизма. При построении совмещенных планов механизма используют метод засечек (рис. 3.1).

Для построения графиков скоростей и ускорений (рис. 3.1) выбираются полюсные расстояния h_u и h_a, где h_u – полюсное расстояние при построении графика скоростей, которое выбирается произвольной длины; рекомендуется его величину выбирать в пределах h_u =30…40 мм; h_a – полюсное расстояние при построении графика ускорений; его рекомендуется принимать в пределах h_a =30…40 мм.

Масштабы времени, скорости и ускорения вычисляют по формулам, вывод которых приводится ниже.

Масштаб времени можно вычислить по формуле

,

где Т – период одного оборота кривошипа, с; L_X – длина отрезка между точками 1 и 1 на графике (диаграмме) перемещений, мм.

Так как период Т можно вычислить по формулам

, или , с,

где – угловая скорость кривошипа, 1/с; n₁ – частота вращения кривошипа, об/мин, то масштаб времени

, с/мм.

Масштаб скорости можно вывести из условия, что скорость исследуемой точки является производной перемещения S по времени:

.

Здесь предполагается, что масштаб перемещений 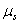и масштаб времени 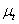являются постоянными величинами.

Так как , то , отсюда

, .

Масштаб ускорения, вывод которого аналогичен предыдущему, вычисляется по формуле

, .

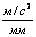Для определения величины скорости или ускорения в каком-либо положении точки В необходимо длину ординаты соответствующего графика умножить на масштаб 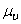или 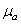соответственно.

 

21.Метод кинематических диаграмм. Покажите использование метода на примере.

 

Рассматриваемый метод позволяет при заданной любой из этих диаграмм без значительных усилий получить другие. Методом кинематических диаграмм часто пользуются для наглядности и выявления возможных ошибок при вычислении. Преимущества этого метода — легкость и то, что результатом является наглядное графическое изображение изменения одного из кинематических параметров движения от времени, или обобщенной координаты. Стоит иметь в виду, что методы графического дифференцирования и интегрирования не всегда могут обеспечивать достаточную точность результатов.

Отметим, что к графическому дифференцированию и интегрированию необходимо порой обращаться даже в тех случаях, когда кинематическая функция задана аналитически, но не имеет достаточно простых формул для определения производной или интеграла.

Графическое дифференцирование. Метод касательных. Графическое дифференцирование используется, когда есть график функции, а нужно получить график ее производной. Так, например, построен график перемещения ползуна кривошипно-повзунного механизма (рис. 2.3), а необходимо построить графику скорости, ускорения.