ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Глава 5 Интегральное исчисление
функции одной переменной
Лекция 21 Первообразная, неопределенный интеграл
План лекции
Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Табличное интегрирование. Свойство инвариантности формул интегрирования. Подведение под знак дифференциала. Замена переменной в неопределенном интеграле. Интегрирование по частям. Разложение многочленов на множители. Разложение правильных рациональных дробей на простейшие. Интегрирование простейших и рациональных дробей. Интегрирование тригонометрических функций и некоторых иррациональных выражений.
Понятие первообразной и неопределенного интеграла
Что такое интеграл? Правда ли, что интегрирование – это действие, обратное дифференцированию. Давайте ответим на эти и другие вопросы.
Определение 1. Первообразной для функции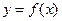 
называется функция 
, такая что 
.
Итак, первообразная – это функция, производная от которой равна заданной функции. Заметим, что первообразная для заданной функции не определяется однозначно. Например, производная от функции 
равна функции 
. Следовательно, функция является первообразной для функции . Но ведь производная от функции 
также равна функции . Следовательно, функция также является первообразной для функции , как и функция 
, где 
- произвольная постоянная.
Теорема 1. (Общий вид первообразных для заданной функции) Пусть функция является первообразной для функции 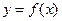. Тогда любая первообразная функции 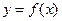представляется в виде 
, где - произвольная постоянная. И наоборот, при любом функция является первообразной для функции .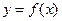
Доказательство. Вторая часть теоремы очевидна, т. к. очевидно, 
. Теперь достаточно доказать, что, если производные двух функций равны, то эти функции отличаются на константу. По сути, достаточно доказать, что если производная от функции (разности упомянутых функций) равна 0, то это производная от константы. Но это действительно так. Возьмем любые две точки. Разность значений функции в этих точках по формуле конечных приращений Лагранжа равна производной в некоторой промежуточной точке, умноженной на разность аргументов (
). Но ведь производная везде равна 0, следовательно, и приращение функции всегда равно 0, т. е. функции равна константе. Теорема доказана.
Определение 2. Совокупность всех первообразных для функции 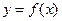называется неопределенным интегралом от функции 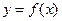и обозначается символом 
.
Итак, действительно, вычислить неопределенный интеграл – это означает выполнение действия, обратного вычислению производной. Кроме того, с учетом теоремы 1, справедлива формула для вычисления неопределенного интеграла 
, (1) где 
- одна из первообразных для функции 
, которая называется под ы нтегральной функцией.
Мы уже знаем, что производная функции имеет многочисленные приложения. Речь в приложениях, конечно идет о значении производных в отдельных точках, т. е. о числах. Обратите внимание, что неопределенный интеграл – это совокупность функций. Поэтому непосредственное применение неопределенного интеграла весьма ограничено. В приложениях встречаются другие виды интегралов, где результатом является число, а технически вычисление сводится к нахождению первообразной функции. Поэтому очень важно научиться вычислять неопределенный интеграл.
1. От каких функций можно вычислить
неопределенный интеграл
Мы знаем, что можно вычислить производную любой элементарной функции, используя таблицу производных основных элементарных функций и правила вычисления производных (производная суммы, разности, произведения, частного, сложной функции).
Отсюда можно написать таблицу первообразных, прочитав таблицу производных «справа налево». Можно также сформулировать правила, соответствующие правилам вычисления производной. С суммой, разностью, вынесением числового множества правила дифференцирования и интегрирования идентичны. А вот с произведением, частным и вычислением производной сложной функции ситуация сложнее. Ведь производная, скажем, произведения не равна «произведению производных». Поэтому таблица первообразных и правила вычисления первообразных не позволяют найти первообразную любой элементарной функции. Существуют, так называемые, «не берущиеся» интегралы от элементарных функций. Например, казалось бы, простой интеграл 
нельзя в нашем понимании вычислить, т. к. среди элементарных функций нет функции, производная от которой равна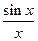 
. Первообразная для непрерывной функции существует всегда, но в данном случае она не среди элементарных. Такие функции называются специальными. Многие из них нужны в приложениях, и их изучают особо.
Итак, в отличии от вычисления производной функции, от нас не требуется умение вычислить неопределенный интеграл от любой элементарной функции. Мы изучим определенные типы элементарных функций, от которых должны научиться вычислять неопределенные интегралы.
Таблица простейших неопределенных интегралов
Давайте вспомним таблицу производных основных элементарных функций:
1) 
| 2) 
| 3) 
| 4) 
|
5) 
| 6) 
| 7) 
| 8) 
|
9) 
| 10) 
| 11) 
| 12) 
|
Во многом она порождает таблицу простейших неопределенных интегралов. Здесь есть и другие интегралы. Все они легко могут быть проверены вычислением производной от правых частей.
1) 
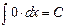
| 2) 
| 3) 
|
4) 
| 5) 
| 6) 
|
7) 
| 8) 
| 9) 
|
10) 
| 11) 
| 12) 
|
13) 
| 14) 
| 15) 
|
