Первое начало термодинамики для атмосферы

ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ В АТМОСФЕРЕ

 

Первое начало термодинамики для атмосферы

Атмосфера представляет собой воздушную среду, в которой постоянно осуществляется переход энергии из одного вида в другие. Раздел метеорологии, рассматривающий общие закономерности преобразования энергии и изменения состояния атмосферы под влиянием притока тепла называется термодинамикой атмосферы.

В этом разделе широко используются выводы, вытекающие из первого начала термодинамики или закона сохранения энергии:

ü Невозможно возникновение или уничтожение энергии, возможен лишь переход одних видов энергии в другие.

Количественно это положение выражается в виде

уравнения первого начала термодинамики или

уравнения притока тепла.

Для вывода этого уравнения выделим в атмосфере частицу сухого воздуха единичной массы. К характеристикам, определяющим состояния этой частицы относятся р_i, ρ_i, T_i, а к характеристикам, определяющим состояние окружающего эту частицу воздуха р_е, ρ_е, Т_е.

В силу малой скорости движения частицы (по сравнению со скоростью звука), можно ввести допущение, что между характеристиками окружающего воздуха и выделенной частицы выполняются квазистатические условия, т. е.: р_i = p_e= p.

Рассмотрим изменение характеристик выделенной частицы при получении этой частицей количества тепла, равного dg. Это количество тепла будет израсходовано на увеличение внутренней энергии и

совершение работы на увеличение объема, занимаемого данной частицей.

В этом случае ее внутренняя энергия увеличится на d u и совершится работа dw против внешних сил давления на увеличение объема:

dg = du_i + dw_i. (3.1)

Для идеального газа, к которому можно отнести и сухой и влажный ненасыщенный воздух, изменение внутренней энергии частицы справедливо выражение:

du_i = c_v · dT_i,(3.2)

где c_v - удельная теплоемкость сухого воздуха при постоянном объеме (v = const). Работа по расширению объема частицы определяется из выражения:

dw_i = p dv_i, (3.3)

где dv_i– приращение объема частицы.

С учетом полученных выражений (3.2) и (3.3) уравнение первого начала термодинамики для выделенного объема воздуха примет вид:

dg = c_v · dT_i + p dv_i, (3.4)

После преобразования выражения (3.4) получим:

dg = (c_v + R_c) · dT_i – v_i · dp (3.7)

Для изобарического процесса (dр = 0) выражение (3.7) примет вид:

dg = (c_v + R_c) · dT_i. (3.8)

Для данного вида процесса справедливо выражение:

dg = c_p · dT_i, (3.9)

где с_р - удельная теплоемкость воздуха при постоянном давлении.

Таким образом:

c_v + R_c = c_p (3.10)

или

с_v – c_p = R_c. (3.11)

Соотношение (3.11) носит название уравнения Майера.

Для сухого воздуха: c_v = 718 Дж/кг К, а с_p = 1006 Дж /кг К,

в этом случае:

с_p – с_v = 288 Дж/кг К (3.12)

или

. (3.13)

Подставим (3.10) в (3.7), тогда с учетом (3.5) получим

уравнение первого начала термодинамики:

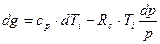. (3.14)

 

3. 2. Адиабатический процесс

Термодинамический процесс называется адиабатическим, если он протекает без теплообмена частицы с окружающей средой.

При адиабатическом процессе dg = 0. Для такого процесса уравнения

(3.4) и (3.14) принимают вид:

p · dg = c_v · dT_i, (3.15)

. (3.16)

Уравнение (3.15) показывает, что при адиабатическом процессе работа против внешних сил давления совершается только за счет внутренней энергии.

При этом, если работа положительная, т.е. направленная на расширение объема (dv_i > 0), то внутренняя энергия частицы уменьшается (dТ_i < 0), и наоборот, при уменьшении объема (сжатие частицы dv_i > 0), ее внутренняя энергия растет (d Т_i > 0).

При подъеме частицы объем ее увеличивается (dv_i > 0), а давление падает (dр < 0). Из уравнений (3.15) и (3.16) следует:

Ø в случае адиабатического подъема температура частицы

всегда понижается (dТ_i < 0).

3.3. Сухоадиабатический градиент

Рассмотрим характер изменения температуры в адиабатически подни­мающейся частице сухого воздуха. Для этого воспользуемся

уравнением первого начала термодинамики:

(3.17)

и выразим изменение давления 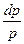через уравнение статики атмосферы, учтя при этом, что р = р_i = р_е

dp = – g· (318)

Заменим в (3.18) через уравнение состояния сухого воздуха???

в результате получим:

(3.19)

Подставим (3.19) в (3.17) и после сокращения запишем:

(3.20)

Разделим выражение (3.20) на выражение (c_p · dz):

(3.21)

Полученное выражение (3.21) определяет изменение температуры воздушной частицы, отнесенное к единице высоты при адиабатическом процессе.

ü Данное выражение показывает, что при адиабатическом подъеме воздушной частицы температура ее всегда падает

Это связано с тем, что при подъеме воздушной частицы происходит расход внутренней энергии на работу расширения.

Сухоадиабатическимградиентом называется падение температуры при адиабатическом подъеме сухой воздушной частицы, отнесенное к единице высоты:

. (3.22)

Подставим (3.22) в (3.21) и получим:

(3.23)

Для реальной атмосферы 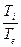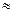1. Следовательно, сухоадиабатический

градиент для реальной атмосферы – величина постоянная (const).

Она выражается:

(3.24)

и равна 0,98°/100 м.

Приближенно можно считать, что температура адиабатически подни­мающейся воздушной частицы падает примерно на один градус при подъеме на каждые 100 м высоты.

Изменение с высотой температуры адиабатически поднимающейся воздушной частицы графически изображается в осях координат – температура – высота, в виде прямой линии. Она называется сухоадиабатой или кривой состояния сухой воздушной частицы.

3.4. Потенциальная температура

Потенциальной температурой () называется температура, которую примет воздушная частица, если ее переместить сухоадиабатически с исходного уровня до уровня с давлением 1000 гПа.

Приближенное выражение для расчета потенциальной температуры имеет вид:

(3.25)

где р₀ – давление воздуха на поверхности Земли;

Т_i – температура воздуха на исходной поверхности;

z – расстояние перемещения частицы по вертикали.

В выражении (3.25) последнее слагаемое правой части представляет собой изменение температуры частицы при перемещении ее от поверхности Земли до уровня 1000 гПа.

Если давление воздуха у поверхности Земли менее 1000 гПа, то уровень 1000 гПа лежит ниже поверхности Земли. Поэтому при дополнительном перемещении частицы от поверхности земли до уровня 1000 гПа частица нагревается.

Потенциальная температура обладает важными свойствами.

§ При сухоадиабатическом перемещении частицы ее потенциальная температура сохраняет постоянное значение, хотя ее температура (как степень нагретости) изменяется.

Это свойство сохранения (консервативности) потенциальной темпера­туры используется в качестве характеристики воздушных масс и оценки их вертикальных перемещений.

§ Если при перемещении частицы ее потенциальная температура изменилась, то это свидетельствует о притоке, либо оттоке тепла.

Другим свойством потенциальной температуры является ее связь с пол­ной энергией воздушной частицы.

§ При адиабатическом перемещении частицы ее полная энергия не изменяется.

 

3.5. Критерии устойчивости атмосферы на основе метода частицы

Распределение температуры окружающего частицу воздуха в различных слоях атмосферы характеризуется вертикальным градиентом температуры

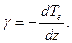(3.26)

Распределение температуры и других метеорологических величин по высоте называется стратификацией атмосферы.

Для определения устойчивости к движению воздуха выделим в атмо­сфере воздушную частицу единичного объема. Характеристикой изменения температуры частицы является сухоадиабатический градиент при ее адиабатическом перемещении.

При вертикальном движении частицы возможны три случая с разными соотношениями между вертикальным и сухоадиабатическим градиентами.

Первый случай: > _а. Данное соотношение свидетельствует о том, что температура воздуха в атмосфере падает с высотой быстрее, чем на 1°С/100 м. На воздушную частицу действуют две силы: сила тяжести и сила Архимеда. Результирующая величина этих сил называется силой плавучести.

При _е > _i, эта сила направлена вверх, а при _е < _i – вниз. Под влиянием силы плавучести частица движется с ускорением, которое выражается формулой:

(3.27)

Если сухую частицу переместить с исходного уровня, на котором

Т_i = Т_е, а , на нижележащий уровень, то ее температура окажется ниже температуры окружающего воздуха, а плотность – выше плотности окружающего воздуха. В этом случае частица будет перемещаться с ускорением вниз.

Таким образом, при смещении частицы с исходного уровня, она про­должит движение со скоростью и ускорением в ту сторону, куда она сместилась в начальный момент.

При этом скорость по абсолютной величине тем больше, чем дальше частица смещается от исходного уровня.

Равновесие частицы в исходном положении неустойчивое.

Стратификация атмосферы при > _а называется сухонеустойчивой.

Второй случай: = _а. В этом случае при перемещении частицы с исходного уровня, на котором Т_i = Т_е, а ,на любой другой уровень, температура и плотность частицы будут равны температуре и плотности окру­жающего ее воздуха. В соответствии с выражением (3.27) ускорение ее дви­жения будет равно нулю.

Термическое состояние атмосферы в этом случае при называется сухобезразличной (равновесной) стратификацией

Третий случай: < _а. Температура с высотой падает медленнее чем на 1°С/100 м. В этом случае при перемещении частицы с исходного уровня, на котором Т_i = Т_е, а , на вышележащий уровень температура частицы будет ниже температуры окружающего ее воздуха, а плотность ее больше плотности воздуха. Частица получит отрицательное ускорение, и будет пе­ремещаться обратно. При перемещении ее на нижележащий уровень ее тем­пература окажется выше, а плотность меньше окружающего воздуха. Частица приобретет положительное ускорение, и возвратится на исходный уровень.

При такой стратификации, на какой бы уровень частица не перемещалась, она будет возвращаться на исходный уровень, после прекращения действия внешних сил.

Стратификация атмосферы при < _а называется сухоустойчивой.

В отдельных слоях атмосферы могут наблюдаться аномальные случаи сухоустойчиной стратификации:

- первый случай – изотермия – >0;

- второй случай – инверсия – <0.

При устойчивой стратификации, а при инверсии в особенности, перемещение частиц по вертикали затруднено, а в случае инверсии – полностью исключено.

При неустойчивой стратификации в атмосфере создаются благоприят­ные условия для возникновения и развития вертикальных движений воздушных частиц.

Данный метод анализа термодинамической устойчивости основан на исследовании поведения индивидуальной частицы. Поэтому его называют методом частиц. Ограничением данного метода является предположение о том, что вертикальное перемещение частицы происходит без теплообмена с окружающей средой, т.е., по адиабатическому закону. В реальных условия атмосферы существует теплообмен между частицей и окружающей ее средой. Но несмотря на это, с качественной стороны, полученные выводы справедливы и для реальной атмосферы.

 

3 .6. Влажноадиабатические процессы

Влажноадиабатическим процессом называется адиабатический про- цесс, протекающий во влажном насыщенном воздухе.

При таком процессе происходит конденсация водяного пара или испа­рение капель воды. Термодинамические процессы в этом случае отличаются от аналогичных процессов, протекающих в сухом воздухе.

Чтобы убедиться в этом, рассмотрим адиабатический подъем влажного воздуха. До тех пор пока влажный воздух не достиг состояния насыщения его состояние изменяется по сухоадиабатическому закону. Температура частицы уменьшается на 1°С/100 м, доля водяного пара постоянна, увеличивается только относительная влажность, вследствие охлаждения частицы.

Границей сухоадиабатического подъема является уровень конденсации, т.е., уровень, на котором влажный ненасыщенный воздух достигает состояния насыщения (относительная влажность равна 100%).

При подъеме частицы выше этого уровня понижение температуры про­должается и начинается процесс конденсации водяного пара. Этот процесс сопровождается выделением скрытой теплоты парообразования (2500 кДж при конденсации одного кг водяного пара). Выделенная теплота, в конечном итоге, расходуется на нагревание этой частицы.

В результате этого нагревания температура частицы выше уровня кон­денсации понижается медленнее.

Кривая состояния насыщенной частицы при ее адиабатическом подъеме называется влажной адиабатой, а изменение температуры частицы при подъеме на единицу высоты при влажноадиабатическом процессе – влажноадиабатическим градиентом у_а.

При влажноадиабатическом процессе наблюдаются следующие эффекты:

- температура поднимающейся частицы уменьшается с высотой мед­леннее, чем при сухоадиабатическом процессе ( '< );

- доля водяного пара, вследствие его конденсации, уменьшается с вы­сотой;

- относительная влажность поднимающегося воздуха постоянна и равна 100%.

Адиабатический подъем влажного воздуха до достижения состояния насыщения (до уровня конденсации) называется сухой стадией, а в состоянии насыщения (выше уровня конденсации) – влажной стадией.