МАГНИТНЫЕ ЦЕПИ. ЗАКОНЫ И ПАРАМЕТРЫ
МАГНИТНЫХ ЦЕПЕЙ
Понятие магнитной цепи
Контур с током или катушка с числом витков 
, по которой протекает ток 
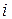, являются источниками магнитного поля (рис.6.1). Для определения характеристик магнитного поля (вектора 
магнитной индукции или вектора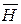 
напряженности магнитного поля) в любой точке пространства необходимо решить достаточно сложную задачу расчета электромагнитного поля.
В электрических цепях удается создать пути для электрического тока, что является результатом весьма большого различия удельной проводимости 
проводников и проводимости 
окружающей их изолирующей среды (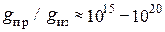
). Поэтому можно пренебречь током утечки в изолирующей среде и считать, что весь ток протекает только по проводнику. Подобно тому, как это делается в электрических цепях, стремятся создать определенный путь и для магнитного потока. Экспериментально установлено, что магнитные силовые линии стремятся проходить в среде с большим значением магнитной проницаемости 
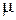(такие среды называют ферромагнетиками). Располагая тела из ферромагнитного материала 
в среде со значительно меньшей магнитной проницаемостью, например, в воздухе или в немагнитном материале с проницаемостью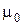 
(
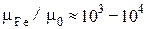), создают определенный путь для прохождения магнитного потока. В дальнейшем магнитную проницаемость ферромагнитных веществ будем обозначать символом 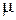, опуская индекс “Fe”.
Магнитной цепью называется совокупность устройств, содержащих ферромагнитные тела, по которым замыкаются линии вектора магнитной индукции и которая может быть описана на основе интегральных понятий о магнитодвижущей силе (м.д.с.) 
и магнитном потоке 
.
Примером простейшей магнитной цепи является катушка с замкнутым ферромагнитным сердечником (рис.6.2). Магнитный поток 
, протекающий по сердечнику, называется основным магнитный потоком.
Так как отношение 
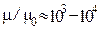, характерное для магнитных цепей, не столь значительно, как отношение проводимостей проводников и изолирующей среды для электрических цепей, то следует учитывать, что часть магнитного потока замыкается по воздуху. Этот магнитный поток назовем магнитным потоком рассеяния 
.
Наличие потока рассеяния приводит к необходимости рассматривать магнитные цепи в общем случае как цепи с распределенными параметрами поскольку магнитный поток различен во всех сечениях сердечника.
Еще одним важным свойством магнитных цепей является их нелинейность. Действительно, магнитная проницаемость 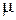ферромагнетиков зависит от напряженности магнитного поля (
) и, следовательно, от токов контуров и катушек, создающих это поле. В сильных полях с увеличением напряженности магнитного поля в сердечнике магнитная проницаемость 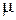материала сердечника существенно уменьшается. Это обстоятельство приводит к увеличению отношения потока рассеяния к основному потоку. При 
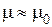разделение потока на основной поток и поток рассеяния теряет смысл. Одновременно теряет смысл понятие о магнитной цепи, и задача о распределении векторов и 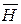в пространстве должна в этом случае ставиться и решаться как задача расчета электромагнитного поля.
При переменной м.д.с. в соответствии с законом электромагнитной индукции проявляется эффект перераспределения магнитного потока по сечению. Вследствие этого в сердечнике создаются области с различной напряженностью магнитного поля и, следовательно, различной магнитной проницаемостью. Это обстоятельство еще более затрудняет расчеты магнитных цепей при рассмотрении всего комплекса электромагнитных явлений, протекающих в них. В то же время, значительные упрощения могут быть получены при сужении круга рассматриваемых явлений.
Таким образом, обоснованное применение понятия о магнитной цепи и математического аппарата ее расчета возможно лишь при правомерности целого ряда упрощающих предположений.
В дальнейшем будем предполагать справедливость следующих допущений:
· считаем, что магнитная проницаемость цепи не зависит от напряженности магнитного поля и, следовательно, от тока, т.е. будем рассматривать магнитную цепь как линейную;
· пренебрегаем потоками рассеяния 
, рассматривая магнитную цепь как цепь с сосредоточенными параметрами;
· считаем, что основной магнитный поток 
равномерно распределен по сечению магнитопровода.
Законы и параметры магнитных цепей
Определим магнитный поток 
для сердечника с постоянным поперечным сечением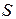 
(рис. 6.3), считая м.д.с. 
катушки известной.
Учитывая допущение о равномерном распределении потока по сечению, из определения магнитного потока получим для рассматриваемой магнитной цепи
Применяя закон полного тока в интегральной форме к контуру 
, являющемуся средней линией сердечника, можем записать
Используя допущение о неизменности потока вдоль контура при постоянном сечении 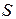, получим
Соотношение 
, с учетом полученных ранее выражений, приводит к равенству
Отношение магнитодвижущей силы (м.д.с.) вдоль всей магнитной цепи к магнитному потоку называют магнитным сопротивлением такой цепи
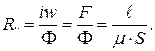
Размерность магнитного сопротивления [ 
] = 1/Гн.
Понятие магнитного сопротивления можно ввести и для участка магнитной цепи. В этом случае 
представляет собой длину участка магнитопровода с сечением 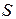. Магнитное сопротивление является основным параметром магнитной цепи.
Соотношение
связывающее магнитный поток, м.д.с. и магнитное сопротивление сердечника, называют законом Ома для магнитной цепи.
Полученное выражение аналогично закону Ома для электрической цепи
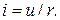
Сравнивая интегральные характеристики магнитных и электрических цепей, можно установить аналогию между ними.
Таблица 6.1
| Магнитная цепь | Электрическая цепь |
Магнитный поток 
М.д.с. 
М.д.с.
на участке АВ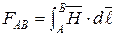 
Магнитное сопротивление 
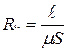Закон Ома для участка
магнитной цепи 
Схема магнитной цепи
| Электрический ток 
Э.д.с. 
Напряжение
на участке АВ 
Электрическое сопротивление 
Закон Ома для участка
электрической цепи 
Схема электрической цепи
|
Расчет магнитной цепи
Рассмотрим магнитную цепь (рис. 6.4), состоящую из последовательных участков с различными сечениями 
, различными магнитными проницаемостями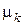 
и воздушным промежутком 
. Величина воздушного зазора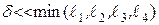 
.
При расчете магнитной цепи выделяют участки магнитной цепи с постоянным сечением, постоянной магнитной проницаемостью и одинаковым магнитным потоком вдоль участка. Каждый участок характеризуется магнитным сопротивлением 
, где длину участка 
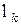можно вычислять вдоль линии, проходящей через середину сечений стержней магнитопровода
При малой длине зазора конфигурация поля в нем существенно не отличается от конфигурации поля в прилегающем участке магнитопровода. Поэтому сечение, сквозь которое проходит магнитный поток в зазоре, можно взять таким же, как и сечение прилегающего к зазору ферромагнитного участка цепи.
Для замкнутого контура рассматриваемой магнитной цепи имеем
Обозначим 
- м.д.с. на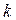 
-м участке магнитной цепи, тогда
или с учетом закона Ома для участка магнитной цепи, получим
Это соотношение, полученное из закона полного тока, остается справедливым для любого контура разветвленной магнитной цепи, т.е. м.д.с. вдоль замкнутого контура магнитной цепи равна сумме произведений магнитного сопротивления на магнитный поток во всех участках (ветвях) цепи, входящих в этот контур.
Последнее уравнение аналогично уравнению второго закона Кирхгофа, составленному для контура электрической цепи при постоянном токе,
В рассматриваемом примере одноконтурной магнитной цепи (рис. 6.4) магнитный поток 
одинаков на различных участках. Следовательно, имеем
причем 
то есть, как и для электрических цепей, магнитное сопротивление последовательно соединенных участков магнитной цепи равно сумме магнитных сопротивлений каждого из участков.
Для напряженности магнитного поля в зазоре можно написать
Эквивалентная схема рассматриваемой магнитной цепи представлена на рис.6.5,
где 
;
Зная магнитную проницаемость вещества сердечника и его размеры, нетрудно рассчитать эквивалентное магнитное сопротивление сердечника и затем при заданной м.д.с. определить магнитный поток
Для разветвленной магнитной цепи (например, рис. 6.6) из условия непрерывности магнитного потока 
с учетом пренебрежения потоками рассеяния следует, что сумма магнитных потоков в участках цепи, отходящих от узла магнитной цепи, равна нулю
Это соотношение аналогично уравнению для узла электрической цепи, записанному согласно первому закону Кирхгофа
Уравнений подобного типа должно быть составлено 
, если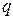 
- число узлов магнитной цепи. Уравнений, составленных по аналогии с уравнениями второго закона Кирхгофа, должно быть 
, где 
- число ветвей магнитной цепи.
Таким образом, расчет магнитных цепей, если можно пренебречь потоками рассеяния и считать магнитную проницаемость материала участков магнитопровода постоянной, аналогичен расчету линейных электрических цепей постоянного тока.
Рассмотрим разветвленную магнитную цепь (рис. 6.6а). Участки магнитной цепи 
, 
, 
(рис. 6.6б) выбраны так, чтобы потоки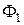 
, 
, 
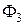вдоль этих участков были постоянными.
Схема замещения рассматриваемой магнитной цепи изображена на рис.6.7. Для этой схемы имеем 
, 
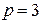, тогда аналог уравнений Кирхгофа для магнитной цепи можно записать следующим образом
где 
.
В результате решения системы уравнений определим магнитные потоки в каждом участке, а через них найдем значения магнитной индукции и напряженности магнитного поля на этих участках.
Аналогия магнитных цепей с электрическими цепями постоянного тока позволяет использовать для расчета магнитной цепи все рассмотренные ранее методы расчета цепей постоянного тока.
Рассмотрим магнитную цепь, в которой имеются катушки с токами в различных ветвях магнитной цепи (рис.6.8а)
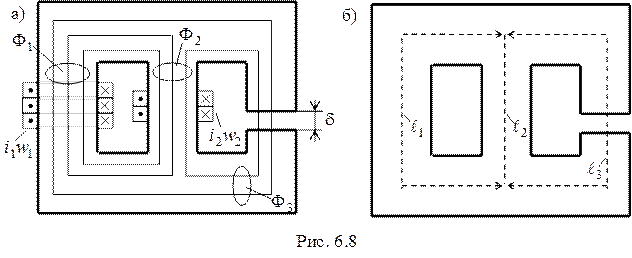
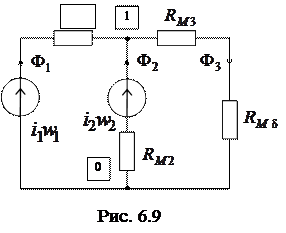Схема замещения магнитной цепи (рис. 6.8а) изображена на рисунке 6.9. Значения магнитных сопротивлений участков цепи определяются из соотношений
Применяя для расчета этой цепи метод узловых напряжений и используя соотношение 
можем записать
Определив из последнего соотношения значение магнитного потока 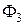, значения остальных потоков получим на основании равенств
Схему замещения магнитной цепи можно также использовать для определения собственных индуктивностей обмоток 
и 
и взаимной индуктивности 
.
В соответствии с определением собственной индуктивности для первой обмотки имеем
где поток 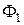создается только током 
в первой обмотке. Рассчитаем схему, изображенную на рис.6.10.
Выражение для потока 
имеет вид
откуда 
.
Взаимную индуктивность 
, в соответствии с определением, рассчитаем из соотношения
Значение магнитного потока 
также определяется из расчета схемы (рис. 6.10), поскольку 
представляет собой потокосцепление со второй обмоткой, создаваемое током в первой.
Можно записать
Окончательно получим
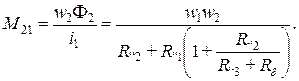
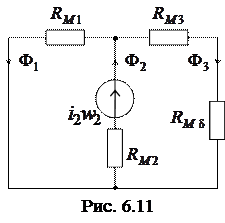
Аналогично проведем расчет собственной индуктивности второй обмотки и взаимной индуктивности 
, для чего используем схему замещения магнитной цепи, изображенную на рис.6.11.
Для собственной индуктивности второй обмотки имеем
причем 
В результате получим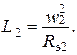 
Взаимную индуктивность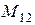 
определим из соотношения
где 
Окончательно имеем 
Отметим, что в обоих случаях получены одинаковые выражения для взаимной индуктивности двух катушек
Поскольку собственные и взаимные индуктивности не зависят от величин токов в обмотках, то в схемах для их расчета (рис. 6.10 и 6.11), значения токов и 
выбираются произвольно. В частности, можно принять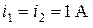 
.
Для иллюстрации приведенных ранее теоретических положений рассмотрим решение нескольких задач.
Задача 1. Определить минимальную силу тока 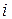электромагнита (рис. 6.12), удерживающего стальной лист массой 
кг, если средний зазор между магнитом и листом, обусловленный неровностями соприкасающихся поверхностей, равен одному миллиметру. Число витков обмотки электромагнита 
, площадь поперечного сечения сердечника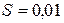 
м2. При решении считать магнитную проницаемость 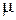вещества сердечника магнита и стального листа бесконечно большой.
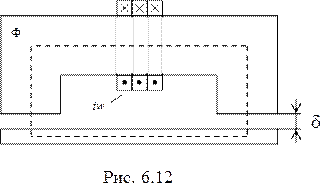
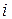Решение. Сопротивление магнитной цепи магнитному потоку , создаваемому током электромагнита, определяется только магнитным сопротивлением зазоров, поскольку магнитные сопротивления участков ферромагнитного сердечника равны нулю (в силу допущения 
).
Величина магнитного потока определяется выражением
Электромагнитную силу, действующую на стальной лист в магнитном поле, определим из соотношения
где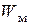 
- энергия магнитного поля системы.
Напряженность магнитного поля в ферромагнетике равна нулю (), поэтому вся энергия магнитного поля 
сосредоточена в области воздушного зазора под полюсами электромагнита.
Считая магнитное поле в зазоре однородным, можно записать
Итак, выражение для электромагнитной силы примет вид
Знак "−" в последнем выражении указывает на то, что сила стремится уменьшить параметр , то есть притянуть стальной лист к электромагниту.
Условием удержания стального листа является неравенство 
отсюда минимальное значение тока, необходимое для этого, равно
А.
Задача 2. Построить линейную эквивалентную схему замещения постоянного магнита (рис.6.13) для рабочего участка характеристики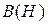 
.
Определить энергию магнитного поля постоянного магнита.
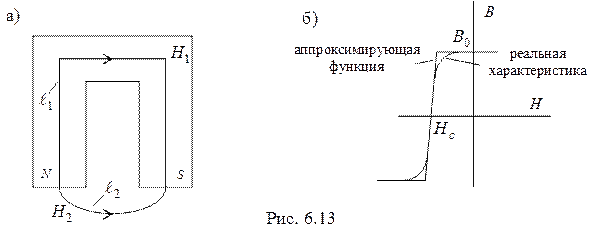
Решение. Для построения линейной эквивалентной схемы замещения постоянного магнита аппроксимируем реальную характеристику 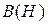на рабочем участке отрезком прямой (рис. 6.13б). В соответствии с законом полного тока имеем
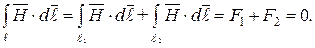
В этом соотношении контур . образован участками 
и 
, совпадающими с линиями напряженности 
и 
внутри магнита и в зазоре, а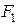 
и 
представляют собой магнитодвижущие силы на этих же участках.
Считая поле в магните однородным, можем записать
С учетом линейной аппроксимации зависимости 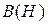, связь напряженности в теле магнита с индукцией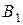 
имеет вид
Домножая обе части последнего равенства на длину участка вдоль средней линии внутри магнита с площадью поперечного сечения 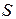, получим
откуда с учетом 
имеем
На основе последнего соотношения можно построить схему замещения постоянного магнита (рис.6.14). Заметим, что магнитный поток , создаваемый постоянным магнитом, зависит от параметров внешней магнитной цепи.
Определим энергию 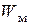однородного магнитного поля в объеме 
длиной и площадью поперечного сечения .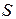
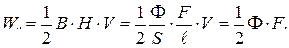
В случае, когда источником однородного магнитного поля является постоянный магнит, энергия магнитного поля определяется выражением
В рассматриваемой задаче энергия магнитного поля магнита может быть определена из соотношения
.
Задача 3. Определить напряженность магнитного поля в зазоре тороидального магнита (рис.6.15). Характеристика материала магнита имеет вид, изображенный на рис. 6.13, б, с параметрами 
А/м,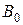 
= 1 Тл, 
. Средний радиус тора 
см, поперечное сечение 
см2.
Решение. Полагая магнитное поле в зазоре однородным, рассчитаем магнитное сопротивление соответственно зазора 
1/ Гн, и магнита 
1/ Гн.
Используя схему замещения постоянного магнита, построенную в предыдущей задаче, изобразим схему замещения постоянного магнита с зазором (рис.6.16).
Для определения напряженности 
магнитного поля в зазоре рассчитаем магнитный поток
причем
Для магнитной индукции в зазоре имеем
Тл,
при этом напряженность магнитного поля в зазоре равна
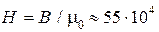А/м.
Задача 4. Система из двух постоянных Г-образных магнитов (рис. 6.17), разделенных выполненным из ферромагнитного материала штифтом, притягивает стальной лист. Определить, во сколько раз отличается сила притяжения при наличии ферромагнитного штифта и без него.
Средний зазор между магнитами и стальным листом = 0,5 мм, а между магнитами и штифтом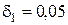 
мм. При расчете считать магнитную проницаемость листа и штифта бесконечно большой. Поперечное сечение магнита 
см2, средняя длина вдоль оси магнитов 
см, длина штифта 
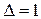см. Параметры характеристики 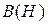материала магнита А/м, 
Тл, .
Решение. Схема замещения рассматриваемой магнитной системы изображена на рис.6.18.
При построении схемы замещения учитывалось, что магнитное сопротивление стального листа равно нулю вследствие бесконечно большого значения магнитной проницаемости материала листа. Нетрудно заметить, что
где 
Электромагнитную силу, действующую на стальной лист, определим из закона сохранения энергии 
так как работа 
, совершенная при перемещении листа на расстояние 
, равна изменению энергии магнитного поля системы. Следовательно, выражение для силы примет вид
Энергию магнитного поля системы можно рассчитать, суммируя энергии, запасенные в постоянных магнитах
Тогда для электромагнитной силы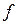 
имеем
Поскольку магнитная проницаемость 
материала штифта принята бесконечно большой, имеем 
. Тогда из последнего соотношения получим выражение для силы 
притяжения листа к постоянным магнитам при наличии штифта
При отсутствии штифта в выражении для силы 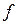следует положить 
. В этом случае значение силы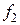 
притяжения листа к постоянным магнитам определится из соотношения
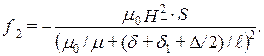
Отношение сил притяжения при наличии штифта и без него получается равным
то есть сила притяжения стального листа к магнитам при наличии штифта увеличивается в 75,6 раза.
Значение силы притяжения листа к магнитам со штифтом приблизительно равно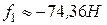 
. Знак "минус" в последнем соотношении указывает, что является силой притяжения.
