Перенос источника э.д.с. Преобразование переноса источника э.д.с. должно быть выполнено таким образом, чтобы уравнения второго закона Кирхгофа оставались неизменными для любого контура схемы. При переносе идеального источника э.д.с. через узел величина и направление э.д.с. сохраняются.
Перенос источника тока. Преобразование переноса источника тока выполняется таким образом, чтобы в любом узле сумма токов осталась без изменения. При переносе идеального источника тока вдоль контура величина его сохраняется, а направление изменяется на противоположное.
Пример 1. Рассчитать токи в ветвях схемы, изображенной на рисунке.
Используя перенос источника э.д.с. через узел, получим схему следующего вида.
Перенос идеального источника э.д.с. через узел позволил упростить схему (стало 3 узла вместо 4), то есть уменьшить на единицу число уравнений Кирхгофа.
Пример 2. В изображенной на рисунке схеме рассчитать токи в ветвях.
Используя перенос идеального источника тока вдоль контура, получим следующую схему
или, преобразуя источники тока в источники э.д.с.,
Используя перенос источника э.д.с. через узел, сводим исходную задачу к расчету двух независимых схем.
Для закрепления изложенного материала рассмотрим решение нескольких задач.
Задача 1. Определить ток 
и напряжение 
в ветви АВ схемы, изображенной на рис.4.4, при замкнутом и разомкнутом ключе. Сопротивления резисторов равны 1 Ом. Величина источника э.д.с. 
В.
Решение. Зададим произвольно условные положительные направления токов в ветвях. Исходная схема при разомкнутом ключе изображена на рис.4.5
Ток = 0, так как ветвь АВ разомкнута. Рассчитывая токи в ветвях схемы, учтем, что при наличии одного источника э.д.с. удобно определить вначале ток 
, используя закон Ома 
где 
- сопротивление всей схемы относительно зажимов источника. Величина определяется путем поэтапного упрощения схемы, показанного на рис.4.6
В результате расчета получим 
Ом, следовательно, ток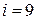 
A. Напряжение на параллельно соединенных резисторах 
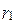и 
рассчитаем следующим образом:
.
Тогда 
. Ток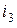 
определим, используя первый закон Кирхгофа 
.
В результате получим следующие значения токов в исходной схеме 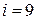А, 
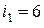А, 
А, 
А, 
.
Для определения напряжения запишем уравнение второго закона Кирхгофа, используя контур (A, B,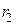 
, 
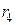, A):
тогда 
В.
Исходная схема при замкнутом ключе изображена на рис.4.7.
Напряжение между точками А и В отсутствует т.е.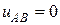 
, так как сопротивление ветви равно нулю. Для определения тока необходимо рассчитать токи в остальных ветвях схемы.
Поскольку 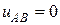, нарисуем схему рис.4.7, объединив узлы А и В в один (рис.4.8).
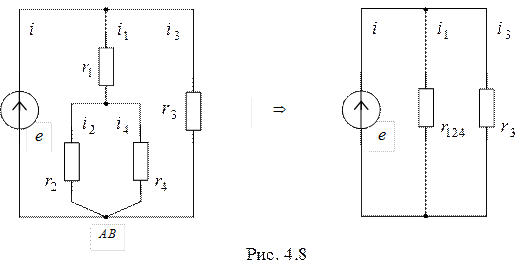
Можно записать
А, 
А,
Тогда 
А.
Напряжение 
на второй и четвертой ветвях, соединенных параллельно, определим из соотношения
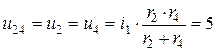В,
а токи во второй и четвертой ветвях вычислим следующим образом:
А, 
А.
Рассчитанные токи в ветвях схемы (рис.4.8) совпадают по направлению с токами в ветвях исходной схемы, поэтому для нее имеем
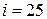А,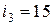 
А, 
А, 
А, 
А.
Ток в ветви АВ (рис.4.7) определим, записав уравнение по первому закону Кирхгофа, например, для узла В
и в результате получим 
А
Задача 2. Определить токи в ветвях схемы (рис.4.9), содержащей зависимый источник э.д.с.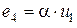 
. Проверить условие баланса мощности. Параметры схемы: 
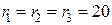Ом; 
; 
A; 
B.
Решение. Определим число независимых уравнений Кирхгофа, которые необходимо сформировать для определения токов в ветвях схемы.
В схеме четыре неизвестных тока (число ветвей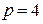 
) следовательно, по законам Кирхгофа необходимо составить четыре уравнения.
Выберем условные положительные направления токов. Схема содержит три узла (
), поэтому по первому закону Кирхгофа составляем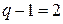 
уравнения. Остальные 
уравнения формируем по второму закону Кирхгофа.
Уравнения первого закона Кирхгофа имеют вид:
для узла 1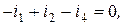 
для узла 2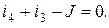 
Для составления уравнений по второму закону Кирхгофа следует выбрать независимые контуры. Направленный граф исходной схемы изображен на рис.4.10.
Пусть дерево графа образовано ветвями 2 и 4. Тогда получим следующие независимые контуры:
контур 1, соответствующий связи 1, образован ветвями 1, 2;
контур 2, соответствующий связи 3, образован ветвями 3, 2, 4.
Направление обхода контуров указано на исходной схеме. Имеем:
для контура 1 
для контура 2 
Зависимый источник э.д.с. учтен в уравнениях Кирхгофа так же, как если бы он был независимым.
С учетом того, что 
, запишем систему уравнений Кирхгофа
После подстановки в эти уравнения численных значений параметров схемы получим следующие результаты:
А, 
А, 
А, 
А.
Составим уравнение баланса мощности. Суммарная мощность, потребляемая приемниками в цепи, равна:
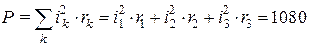Вт.
Суммарная мощность, отдаваемая источниками, равна:
Напряжение 
на зажимах источника тока определим, составив уравнение по второму закону Кирхгофа для контура, включающего в себя резистор 
и источник тока:
Для рассматриваемой цепи получаем
Вт.
Правильность решения задачи подтверждена выполнением условия баланса мощности в цепи
