ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Под электрическими цепями постоянного тока понимают цепи, в которых ток, напряжение, э.д.с. не изменяются во времени. Практически цепи постоянного тока состоят из резистивных элементов и источников энергии. Катушку индуктивности в цепи постоянного тока следует считать короткозамкнутой, так как при постоянном токе 
в катушке не индуцируется э.д.с. самоиндукции 
:
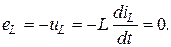
Конденсатор следует рассматривать как разрыв ветви, так как при постоянном напряжении 
на зажимах конденсатора ток в этой ветви отсутствует:
Баланс мощностей
Мощность 
, потребляемая резистором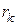 
, определяется по любой из трех формул
Мощность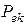 
, отдаваемая источником э.д.с. 
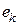, определяется выражением
если условные положительные направления тока и э.д.с. совпадают, и
когда эти направления противоположны.
В отличии от мощности которая всегда положительна, мощность источников 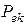может быть и положительной, и отрицательной. Отрицательная мощность получается, если ток в источнике направлен против э.д.с. В этом случае источник э.д.с. фактически является приемником. Такой режим возможен лишь в цепи, где имеется по крайней мере два источника, при этом мощность одного из источников будет величиной положительной.
Мощность 
отдаваемая источником тока 
определяется выражением
если условные положительные направления тока и напряжения противоположны и,
когда эти направления совпадают.
Из закона сохранения энергии следует, что сумма мощностей, рассеиваемых на резисторах цепи, равна сумме мощностей, отдаваемых источниками э.д.с. и тока
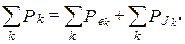
Это соотношение может быть использовано для проверки правильности расчета цепи.
Пример. Схема электрической цепи (рис.3.16) на постоянном токе преобразуется в схему, изображенную на рис.4.1а. Поскольку ток 
эта схема распадается на две несвязанных между собой схемы (рис.4.1 б,в), и ток 
 |
Действительно, для узла 5 согласно первому закону Кирхгофа можем записать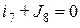 
а для узла 3 имеем 
или 
Для схемы рис.4.1, б по второму закону Кирхгофа
или 
а в схеме рис.4.1, в 
Уравнение баланса мощностей имеет вид:
Подставляя в это уравнение выражения для токов 
и 
и учитывая, что 
, получим тождество.
Определим напряжение на конденсаторе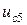 
Для этого составим уравнение по второму закону Кирхгофа для контура (6,4,7,5), выбрав положительный обход контура против часовой стрелки:
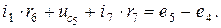
Отсюда 
Преобразования электрических цепей
Для упрощения расчета сложной цепи в ряде случаев целесообразно осуществить преобразование некоторой части цепи. Преобразование будем считать эквивалентным, если токи в ветвях и напряжения на элементах не преобразованной части схемы остаются неизменными. Преобразование цепи целесообразно использовать в тех случаях, когда оно уменьшает число узлов или число независимых контуров.
