Литература: [Л.1], с 40
В качестве примера приведем разложение в ряд Фурье периодической последовательности прямоугольных импульсов с амплитудой 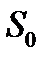 , длительностью
, длительностью 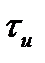 и периодом следования
и периодом следования 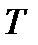 , симметричной относительно нуля, т.е.
, симметричной относительно нуля, т.е.
 , (2.10)
, (2.10)
Здесь 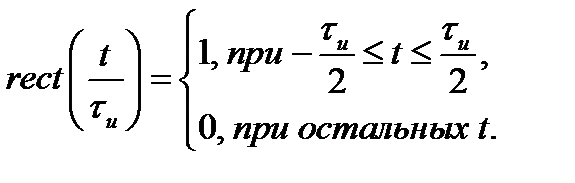
Разложение такого сигнала в ряд Фурье дает
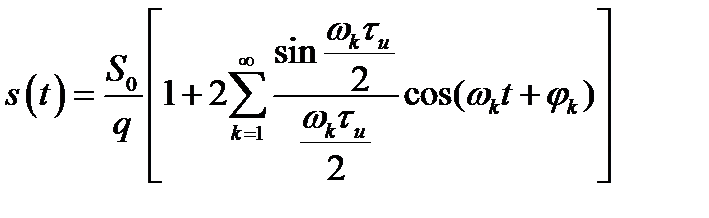 , (2.11)
, (2.11)
где  – скважность.
– скважность.
Для упрощения записи можно ввести обозначение
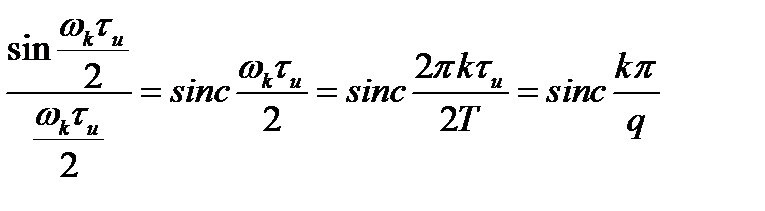 , (2.12)
, (2.12)
Тогда (2.11) запишется следующим образом
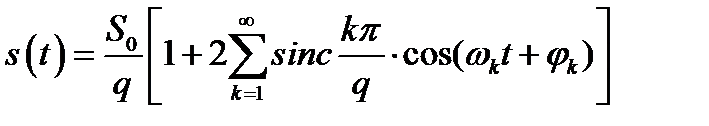 , (2.13)
, (2.13)
На рис. 2.3 изображена последовательность прямоугольных импульсов. Спектр последовательности, как впрочем, и любого другого периодического сигнала, носит дискретный (линейчатый) характер.
Огибающая спектра (рис. 2.3, б) пропорциональна 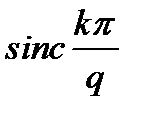 . Расстояние по оси частот между двумя соседними составляющими спектра равно
. Расстояние по оси частот между двумя соседними составляющими спектра равно  , а между двумя нулевыми значениями (ширина лепестка спектра) –
, а между двумя нулевыми значениями (ширина лепестка спектра) – 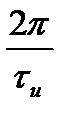 . Число гармонических составляющих в пределах одного лепестка, включая правое по рисунку нулевое значение, составляет
. Число гармонических составляющих в пределах одного лепестка, включая правое по рисунку нулевое значение, составляет 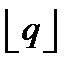 , где знак
, где знак  означает округление до ближайшего целого числа, меньшего
означает округление до ближайшего целого числа, меньшего 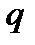 (если скважность – дробное число), или
(если скважность – дробное число), или 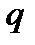 (при целочисленном значении скважности). При увеличении периода
(при целочисленном значении скважности). При увеличении периода 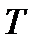 основная частота
основная частота 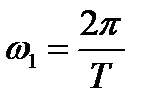 уменьшается, спектральные составляющие на диаграмме сближаются, амплитуды гармоник также уменьшаются. При этом форма огибающей сохраняется.
уменьшается, спектральные составляющие на диаграмме сближаются, амплитуды гармоник также уменьшаются. При этом форма огибающей сохраняется.

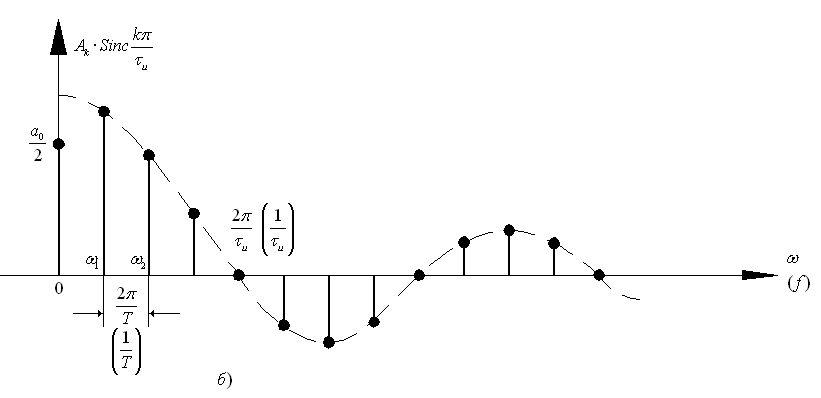
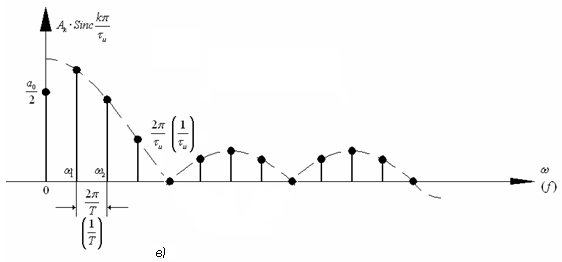

Рис. 2.3
При решении практических задач спектрального анализа вместо угловых частот  используют циклические частоты
используют циклические частоты  , измеряемые в Герцах. Очевидно, расстояние между соседними гармониками на диаграмме составит
, измеряемые в Герцах. Очевидно, расстояние между соседними гармониками на диаграмме составит 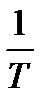 , а ширина одного лепестка спектра –
, а ширина одного лепестка спектра –  . Эти значения представлены на диаграмме в круглых скобках.
. Эти значения представлены на диаграмме в круглых скобках.
В практической радиотехнике в большинстве случаев вместо спектрального представления (рис. 2.3, б) используют спектральные диаграммы амплитудного и фазового спектров. Амплитудный спектр последовательности прямоугольных импульсов представлен на рис. 2.3, в.
Очевидно, огибающая амплитудного спектра пропорциональна  .
.
Что же касается фазового спектра (рис. 2.3, г), то полагают, что начальные фазы гармонических составляющих изменяются скачком на величину -π при изменение знака огибающей sinc kπ/q. Начальные фазы гармоник первого лепестка, полагаются равными нулю. Тогда начальные фазы гармоник второго лепестка составят φ = -π, третьего лепестка φ = -2π и т.д.
Рассмотрим еще одно представление сигнала рядом Фурье. Для этого воспользуемся формулой Эйлера
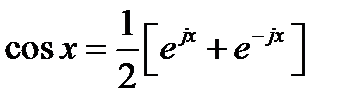 .
.
В соответствии с этой формулой k-ю составляющую (2.9) разложения сигнала в ряд Фурье можно представить следующим образом
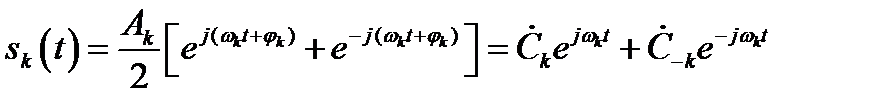 , (2.14)
, (2.14)
где
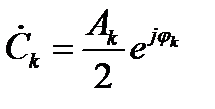 ;
; 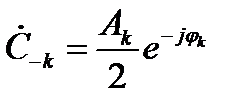 . (2.15)
. (2.15)
Здесь величины 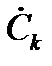 и
и  являются комплексными и представляют собой комплексные амплитуды составляющих спектра. Тогда ряд
являются комплексными и представляют собой комплексные амплитуды составляющих спектра. Тогда ряд
Фурье (2.8) с учетом (2.14) примет следующую форму
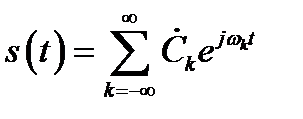 , (2.16)
, (2.16)
где
 , (2.17)
, (2.17)
Нетрудно убедиться в том, что разложение (2.16) проводится по базисным функциям 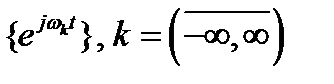 , которые также являются ортогональными на интервале
, которые также являются ортогональными на интервале 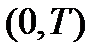 , т.е.
, т.е.

Выражение (2.16) представляет собой комплексную форму ряда Фурье, которая распространяется на отрицательные частоты. Величины  и
и  , где
, где  означает комплексную сопряженную с
означает комплексную сопряженную с 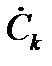 величину, называются комплексными амплитудами спектра. Т.к.
величину, называются комплексными амплитудами спектра. Т.к.  является комплексной величиной, из (2.15) следует, что
является комплексной величиной, из (2.15) следует, что
 и
и  .
.
Тогда совокупность 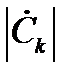 составляет амплитудный, а совокупность
составляет амплитудный, а совокупность 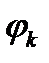 – фазовый спектр сигнала
– фазовый спектр сигнала  .
.

Рис. 2.4
На рис. 2.4 представлена спектральная диаграмма спектра рассмотренной выше последовательности прямоугольных импульсов, представленного комплексным рядом Фурье

Спектр также носит линейчатый характер, но в отличие от ранее рассмотренных спектров определяется как в области положительных, так и в области отрицательных частот. Поскольку  является чётной функцией аргумента
является чётной функцией аргумента 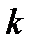 , спектральная диаграмма симметрична относительно нуля.
, спектральная диаграмма симметрична относительно нуля.
Исходя из (2.15) можно установить соответствие между 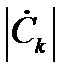 и коэффициентами
и коэффициентами 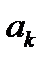 и
и 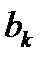 разложения (2.3). Так как
разложения (2.3). Так как
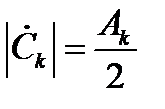 и
и  ,
,
то в результате получим
 . (2.18)
. (2.18)
Выражения (2.5) и (2.18) позволяют найти значения 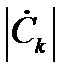 при практических расчетах.
при практических расчетах.
Дадим геометрическую интерпретацию комплексной формы ряда Фурье. Выделим k-тую составляющую спектра сигнала. В комплексной форме k-я составляющая описывается формулой
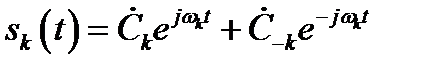 , (2.19)
, (2.19)
где  и
и 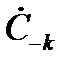 определятся выражениями (2.15).
определятся выражениями (2.15).
В комплексной плоскости каждое из слагаемых в (2.19) изображается в виде векторов длиной 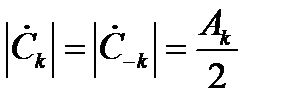 , повернутых на угол
, повернутых на угол 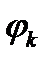 и
и  относительно вещественной оси и вращающихся в противоположных направлениях с частотой
относительно вещественной оси и вращающихся в противоположных направлениях с частотой  (рис. 2.5).
(рис. 2.5).
Очевидно, сумма этих векторов дает вектор, расположенный на вещественной оси, длина которого составляет 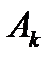 . Но этот вектор соответствует гармонической составляющей
. Но этот вектор соответствует гармонической составляющей


Рис. 2.5
Что касается проекций векторов на мнимую ось, то эти проекции имеют равную длину, но противоположные направления и в сумме дают ноль. А это значит, что сигналы, представленные в комплексной форме (2.16) в действительности являются вещественными сигналами. Иными словами, комплексная форма ряда Фурье является математической абстракцией, весьма удобной при решении целого ряда задач спектрального анализа. Поэтому, иногда спектр, определяемый тригонометрическим рядом Фурье, называют физическим спектром, а комплексной формой ряда Фурье – математическим спектром.
И в заключение рассмотрим вопрос распределения энергии и мощности в спектре периодического сигнала. Для этого воспользуемся равенством Парсеваля (1.42). При разложении сигнала в тригонометрический ряд Фурье выражение (1.42) принимает вид
 .
.
Энергия постоянной составляющей
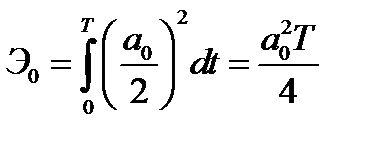 ,
,
а энергия k-той гармоники
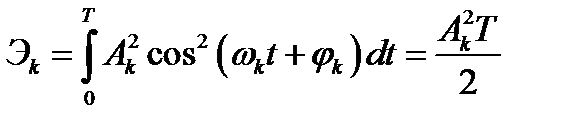 .
.
Тогда энергия сигнала
 . (2.20)
. (2.20)
Т.к. средняя мощность сигнала
 ,
,
то с учетом (2.18)
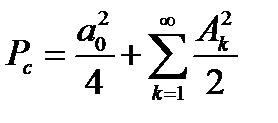 . (2.21)
. (2.21)
При разложение сигнала в комплексный ряд Фурье выражение (1.42) имеет вид
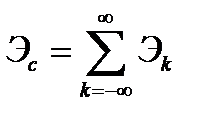 ,
,
где  - энергия k-той гармоники.
- энергия k-той гармоники.
Энергия сигнала в этом случае
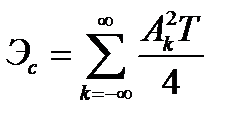 ,
,
а его средняя мощность
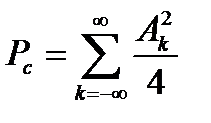 .
.
Из приведенных выражений следует, что энергия или средняя мощность k-той спектральной составляющей математического спектра вдвое меньше энергии или мощности соответствующей спектральной составляющей физического спектра. Это обусловлено тем, что  физического спектра распределяется поровну между
физического спектра распределяется поровну между  и
и  математического спектра.
математического спектра.
Выражения (2.20) – (2.12) позволяют рассчитать и построить спектральные диаграммы распределения энергий или мощностей, т.е. энергетические спектры периодического сигнала.
| -τи/2 |
| τи/2 |
| Т |
| t |
| U0 |
| S(t) |
Задание №1, группа РИ – 210701
Рассчитать и построить спектр амплитуд и спектр фаз периодической последовательности импульсов. U0 = 1 В; τи = 1 мс; Т = 2 мс.
Задание №2, группа РИ – 210601
Рассчитать и построить спектр амплитуд и спектр фаз периодической последовательности импульсов. U0 = 1 В; τи = 1 мс; Т = 4 мс.
| -τи/2 |
| τи/2 |
| Т |
| t |
| U0 |
| S(t) |
| -U0 |
| -τи/2 |
| τи/2 |
| Т |
| t |
| U0 |
| S(t) |
Задание №3, группа РИ – 210501
Рассчитать и построить спектр амплитуд и спектр фаз периодической последовательности импульсов. U0 = 1 В; τи = 1 мс; Т = 2 мс.
Задание №4, группа РИ – 210401
Рассчитать и построить спектр амплитуд и спектр фаз периодической последовательности импульсов. U0 = 1 В; τи = 1 мс; Т = 4 мс.
Задание №5, группа РИ – 210402
Рассчитать и построить спектр амплитуд и спектр фаз периодической последовательности импульсов. U0 = 1 В; τи = 1 мс; Т = 2 мс.
Задание №6, группа РИ –
Рассчитать и построить спектр амплитуд и спектр фаз периодической последовательности импульсов. U0 = 1 В; τи = 1 мс; Т = 4 мс.
| -τи |
| Т |
| t |
| U0 |
| S(t) |






