1.1. Особенности термодинамического поведения
реального газа
В паротурбинных и холодильных установках рабочие тела следует рассматривать как реальные газы. Между свойствами идеального и реального газов имеются существенные различия, обусловленные влиянием сил межмолекулярного взаимодействия и наличием собственного объёма молекул реального газа.
Для анализа поведения реального газа рассмотрим на диаграмме р,v процесс изотермического сжатия реального газа (рис. 1.1). При температурах выше критической (см. табл. 1.1), а также при больших значениях удельного объёма изотермы реального газа близки к равнобочным гиперболам, как у идеального газа. При изотермическом сжатии газа при Т<Ткр его давление монотонно возрастает, пока не достигнет определённого значения, называемого давлением насыщенного пара ps, находящегося в равновесии с жидкостью (процесс 1–2). При дальнейшем сжатии давление пара не изменяется, но он конденсируется –– переходит в жидкое состояние (процесс 2–3). Когда весь пар сконденсируется, начнётся изотермическое сжатие жидкости; здесь давление резко возрастает при незначительном уменьшении удельного объёма (процесс 3–4).
Таблица 1.1. Критические параметры некоторых веществ
| Веще- ство | Параметры | Веще- ство | Параметры | ||||
| Т кр, К | р кр, МПа | ρкр, кг/м3 | Т кр, К | р кр, МПа | ρкр, кг/м3 | ||
| H2 | 33,2 | 1,3 | СО2 | 304,2 | 7,38 | ||
| N2 | 126,2 | 3,40 | NH3 | 405,5 | 11,28 | ||
| O2 | 154,6 | 5,04 | H2O | 647,3 | 22,11 |
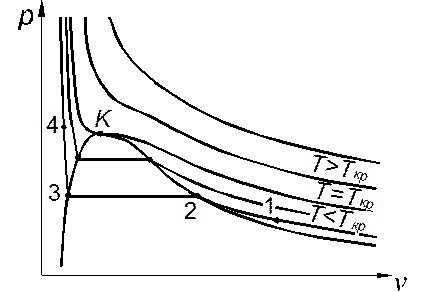Рис. 1.1. Изотермы реального газа на диаграмме p,v.
|
Точки 2 и 3 соответствуют характерным состояниям пара ижидкости при фазовом равновесии: 2 — насыщенному пару, 3 — насыщенной (кипящей) жидкости. Участок 1–2 соответствует паровой ветви изотермы, 3–4 — жидкостной, а участок конденсации 2–3 –– состояниям влажного пара, то есть равновесной смеси паровой и жидкой фаз; на этом участке изотерма одновременно является изобарой.
Значение удельного объёма насыщенного пара v" на большинстве докритических изотерм гораздо больше значения удельного объёма насыщенной жидкости v'. С ростом температуры разность v"– v' уменьшается и становится равной нулю при критической температуре в критической точке К, в которой исчезают различия между свойствами кипящей жидкости и насыщенного пара. Критическая изотерма Т = Т кр на диаграмме p,v имеет в критической точке горизонтальную касательную и точку перегиба, что математически выражается критическими условиями
| (1.1) |
Кривая 2–К–3 на термодинамических диаграммах p,v и T,v, отделяющая область двухфазного состояния (влажного пара) от однофазной, называется пограничной кривой. Она состоит из двух ветвей: пограничной кривой жидкости К–3 на диаграмме p,v и К-2 на диаграмме T,v и пограничной кривой пара К–2 на диаграмме p,v и К-3 на диаграмме T,v, которые плавно сопрягаются в критической точке.
При изобарном подводе теплоты к жидкости, взятой при низкой температуре Т 1, и давлении, меньшем критического, температура жидкости повышается до температуры насыщения Тs=T 2, то есть до температуры фазового равновесия жидкости и пара (процесс 1–2 на диаграмме Т,v, рис. 1.2). Удельный объём жидкости при её нагреве от Т 1до Т 2увеличивается незначительно. При дальнейшем подводе теплоты при постоянном давлении происходит парообразование — фазовый переход вещества из жидкого в парообразное состояние (процесс 2–3). Температура в процессе парообразования остается постоянной и равной Тs. После превращения всей жидкости в пар подвод теплоты приводит к росту температуры пара (к его перегреву).
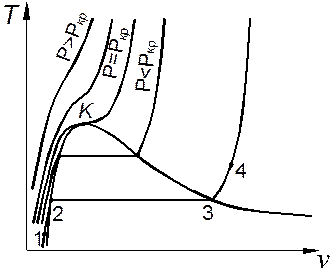Рис. 1.2. Изобары реального газа на диаграмме Т,v.
|
Итак, на докритической изобаре можно выделить три характерных участка: 1–2 — нагрев жидкости до температуры насыщения, 2–3 —парообразование (кипение), 3–4 — перегрев пара. Противоположный процесс — изобарный отвод теплоты –– приводит к охлаждению пара и его конденсации, а при дальнейшем отводе теплоты жидкость охлаждается и затем затвердевает.
С ростом давления увеличивается температура насыщения и уменьшается разность v"– v'. При критическом давлении v' = v" = vкр. Изобара p = p кр в критической точке К имеет горизонтальную касательную и точку перегиба.
Из диаграмм р,v и Т,v видно, что каждому значению давления насыщенного пара ps соответствует определённое значение температуры Ts ё. Кривая ps=f(Ts) на фазовой диа-
грамме р,Т (рис.1.3), соответствующая равновесному сосуществованию жидкости и пара, называется кривой парообразования. Максимальные значения р и Т на данной кривой –– это параметры критической точки К, а минимальные — параметры тройной точки L, в которой находятся в равновесии три фазы: паровая, жидкая и твердая.
Рис. 1.3. Фазовая диаграмма реального газа.
|
На диаграмме р,Т показаны также изохоры, каждая из которых представляет собой линию малой кривизны, исходящую из точки на кривой парообразования. Изохоры пара, которым соответствуют значения v>v кp, расположены правее кривой парообразования 1, а изохоры жидкости при v<v кp — левее. Изохора v=v крисходит из критической точки и имеет в ней общую касательную с кривой парообразования, что выражается правилом Планка-Гиббса
 .
| (1.2) |
Такое термодинамическое поведение реального газа свойственно всем индивидуальным веществам в характерных для каждого из них интервалах изменения параметров. Оно гораздо сложнее поведения идеального газа.
На полной фазовой диаграмме (рис. 1.4) показаны три фазы, разделённые линиями фазового равновесия 0–L, L–К и L–N, сходящимися в тройной точке L. Определив по параметрам Т и р положение точки на диаграмме, можно установить состояние вещества. Положение точки на линии фазового равновесия свидетельствует о том, что сосуществуют две фазы. Линия О–L соответствует равновесию твердой и газообразной фаз, линии L–N и L–К –– равновесию твердой–жидкой и жидкой–газообразной фаз. В критической точке К заканчивается линия равновесия жидкость–пар.
Рис. 1.4. Фазовые диаграммы для веществ, плотность которых при плавлении уменьшается (а) либо увеличивается (б).
|
Для большинства веществ наклон линии равновесия твердое тело–жидкость положителен, как показано на рис. 1.4 а, что обусловлено уменьшением плотности вещества при плавлении. В этом случае повышение давления жидкости при T = const приводит к затвердеванию вещества (линия 1–2 на рис 1.4 а). Однако у некоторых веществ плотность при плавлении возрастает, у них наклон линии равновесия твердое тело–жидкость отрицателен (см. рис. 1.4 6). Пример такого вещества –– вода; лёд при изотермическом сжатии плавится (линия 1–2 на рис. 1.4 6).
На диаграмме р,Т (рис. 1.4) изобарный процесс 3–4 соответствует сначала нагреву твердого тела, затем его плавлению при температуре Т пл и давлении р пл и, наконец, нагреву жидкости. Линия 3–4 пересекает кривую равновесия твёрдое тело–жидкость. При продолжении этого процесса (линия 4–4')происходит нагрев жидкости, парообразование при температуре Т пи давлении р п, а затем перегрев пара. Линия 4–4' пересекает кривую равновесия жидкость–газ. Если давление меньше давления в тройной точке, твердое тело при изобарном нагреве переходит в газообразное состояние, минуя жидкую фазу. Это процесс сублимации (возгонки) 5–6.
У аморфных веществ, не имеющих в твёрдом состоянии кристаллической структуры (например, у воска), переход из твёрдого состояния в жидкое при постоянном давлении происходит при переменной температуре.
1.2. Уравнения состояния и таблицы термодинамических свойств реального газа
Применение методов термодинамики для решения технических задач невозможно без знания термодинамических свойств рабочих веществ. Экспериментальное определение свойств реальных газов –– трудоёмкий процесс, и не все необходимые для расчётов свойства могут быть получены в эксперименте (например, энтропия). В то же время по термическому уравнению состояния p=f (T, v)можно рассчитать не только термические (р, v, T),но и калорические свойства (h, s, cv, cp), так как на основании первого и второго законов термодинамики получены термодинамические соотношения, связывающие эти свойства.
В связи со сложностью термодинамического поведения реальных газов уравнение состояния реального газа имеет сложную структуру. Среди уравнений состояния одно из наиболее простых –– уравнение Ван-дер-Ваальса
 ,
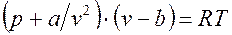| (1.3) |
где а и b — постоянные, учитывающие соответственно парное взаимодействие молекул и их собственный объём.
Это уравнение качественно правильно описывает почти все особенности поведения реального газа. Однако оно даёт большие погрешности вблизи пограничной кривой, в критической области и в области жидкой фазы.
М.П. Вукалович и И.И. Новиков предложили более сложное уравнение состояния, учитывающее объединение молекул в комплексы из двух, трёх и бὀльшего числа молекул. Это явление влияет на свойства вещества в области высоких плотностей. Такое уравнение, использовавшееся для расчета свойств воды и водяного пара, имеет вид
 ,
| (1.4) |
где А 1(Т), А 2(Т), ... — функции температуры,
а и b — постоянные, аналогичные постоянным в (1.3).
Общее уравнение состояния реального газа, теоретически обоснованное Дж. Майером и Н.Н. Боголюбовым методами статистической физики, записывается в форме
| (1.5) |
Функции температуры В (Т), С (Т), ... — вириальные коэффициенты, учитывающие парные, тройные и более сложные взаимодействия молекул. При v →∞ уравнение (1.5) переходит в уравнение состояния идеального газа.
На практике в уравнении (1.5) ряд заменяют полиномом. Функции В (Т), С (Т),... также представляют в виде по-
линомов от 1/ Т, их коэффициенты определяют по опытным данным о термодинамических свойствах вещества.
Уравнение состояния содержит в компактной форме информацию о свойствах вещества и может использоваться для расчётов процессов и циклов с помощью ЭВМ. Однако во многих инженерных расчётах применяются не эти сложные уравнения, а составленные с их помощью таблицы термодинамических свойств и диаграммы состояния. Для воды и водяного пара М.П. Вукалович, С.Л. Ривкин и А.А. Александров рассчитали таблицы свойств, которые широко используются при тепловых расчётах.
На кафедре термодинамики ОИИМФ в 1960–1995 гг. составлены уравнения состояния и рассчитаны таблицы термодинамических свойств воздуха и его компонентов, метана, этана, пропана и других технически важных газов. Ряд таблиц был утверждён Госстандартом СССР в качестве таблиц стандартных справочных данных, обязательных к применению во всех отраслях народного хозяйства.
Для расчёта калорических свойств вещества с помощью уравнения состояния используются термодинамические соотношения, которые получаются из объединённого уравнения I и II законов термодинамики:
 .
| (1.6) |
Для вывода этих соотношений выразим в уравнении (1.6) полные дифференциалы ds и du через частные производные
 .
| (1.7) |
Для частного случая изохорного процесса (dv = 0), учитывая известное равенство (∂ u/∂T) v = cv, из уравнения (1.7) получим
 .
| (1.8) |
Для изотермического процесса (dT = 0) из (1.7) следует
 .
| (1.9) |
Продифференцировав (1.9) по Т при v = const, найдём
 .
| (1.10) |
Для смешанной производной порядок дифференцирования безразличен, и с учетом равенства (1.8) можно записать
 ,
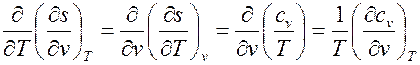| (1.11) |
 .
| (1.12) |
Подставив полученные выражения в (1.10) и исключив одинаковыечлены в левой и правой частях, получим
 .
| (1.13) |
Это выражение представляет собой дифференциальное термодинамическое соотношение, связывающее частные производные термических и калорических величин.
Подставив выражение (1.13) для производной (∂ s /∂ v) T в равенство (1.9), можно записать уравнение для расчета частной производной (∂ u /∂ v) T через термические параметры
 ,
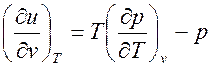| (1.14) |
где правую часть можно вычислить из уравнения состояния.
Дифференцируя соотношение (1.13) по Т и учитывая (1.8), получим
 ,
| (1.15) |
или окончательно
| (1.16) |
Аналогичным путём могут быть получены и другие термодинамические соотношения, связывающие в дифференциальной форме термические и калорические свойства веществ.
Использование термодинамических соотношений для определения калорических свойств можно проиллюстрировать на примере расчёта внутренней энергии на основании соотношения (1.14), интегрируя которое получим
| (1.17) |
При расчётах внутренней энергии в (1.17) следует подставить выражения функций р и (∂ p /∂ T) v, полученные из уравнения состояния p = f (T, v). После подстановки интегрируем при постоянной температуре, в результате чего на каждой изотерме появляется своя постоянная интегрирования φ. Совокупность этих постоянных образует неизвестную функцию φ(T).
Для определения функции φ(T) рассмотрим предельный случай p →0, когда уравнение состояния приобретает вид p = RT / v. Тогда подынтегральное выражение в (1.17) обращается в нуль и видно, что функция φ(T) является внутренней энергией идеального газа. Окончательно получим
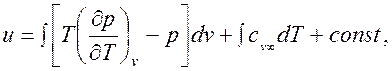
| (1.18) |
где постоянная интегрирования определяется началом отсчёта внутренней энергии идеального газа. Аналогично из соотношений (1.13) и (1.16) можно получить выражения для расчёта энтропии и изохорной теплоемкости реального газа
| (1.19) |
| (1.20) |
Взяв вторую форму основного уравнения термодинамики, представленную через переменные Т и р, запишем объединённое уравнение обоих законов термодинамики в виде
| (1.21) |
На основании уравнения (1.21) можно получить дифференциальные термодинамические соотношения при переменных Т и р. Для их использования необходимо располагать уравнением состояния в форме v = F (T, p).
Термодинамические соотношения имеют важное прикладное и теоретическое значение. Они позволяют на основании термического уравнения состояния вещества рассчитывать его калорические свойства, которые экспериментально определяются сложнее и менее точно, чем термические свойства. Это сокращает объём трудоёмких экспериментальных исследований калорических свойств и в тоже время позволяет составлять подробные таблицы термодинамических свойств реальных газов.
Хорошее согласование рассчитанных значений калорических свойств с опытными данными свидетельствует о точности и взаимной согласованности использованных данных о термических и калорических свойствах вещества, а также о строгости термодинамических соотношений и справедливости I-го и II-го законов термодинамики, на основании которых они получены. Последнее обстоятельство определяет теоретическое значение этих соотношений.
Таблицы свойств пара и жидкости в состоянии насыщения являются однопараметрическими, поскольку свойства на пограничной кривой определяются одним параметром состояния. В качестве независимой переменной выбирают либо температуру, либо давление.
Таблицы свойств однофазной области (в состоянии жидкости либо пара) составляют в зависимости от двух переменных — давления и температуры 
. Иногда в верхней части таблицы для каждой изобары повторяют данные о свойствах насыщенных пара и жидкости, что позволяет решать ряд задач, не прибегая к таблицам для состояния насыщения. Жирная горизонтальная линия в таблице на изобарах при давлениях ниже критического разделяет данные о свойствах жидкости и перегретого пара.
Таблицы составляют с такими шагами по температуре и давлению, которые позволяют применять линейную интерполяцию при промежуточных значениях Т и р.
Используя данные для состояния насыщения, можно определять свойства влажного пара, если известна степень сухости, то есть массовая доля насыщенного пара во влажном паре. Тогда 1 кг влажного пара как смеси содержит (1- х)кг насыщенной жидкости и х кг насыщенного пара. Свойства этих фаз обозначают одним и двумя штрихами. Определив по таблицам для заданной температуры либо давления значения v', v", h', h", s', s",можно рассчитать свойства влажного пара по правилу аддитивности:
  ,
| (1.22) |
 ,
| (1.23) |
 .
| (1.24) |
При малых давлениях (температурах) v" намного больше v' и значения vx можно рассчитывать по формуле vx≈v"x.
Разность h" – h' = r — это количество теплоты, подведенной в процессе фазового перехода вещества из состояния кипящей жидкости в состояние насыщенного пара. Величина r называется теплотой парообразования; она уменьшается с ростом давления насыщенного пара и равна нулю при р = ркр. В таблицах обычно даны значения r,их удобно использовать при расчёте по формуле (1.23).
1.3. Термодинамические диаграммы реального газа
Для облегчения расчётов процессов с реальным газом используют термодинамические диаграммы, построенные по табличным данным. Достоинство диаграмм по сравнению с таблицами –– наглядность, позволяющая проводить качественный анализ процессов и циклов, а недостаток — меньшая точность. На практике большую роль играет изоэнтропный процесс, поэтому широкое распространение получили энтропийные диаграммы Т, s и h, s,на которых этот процесс изображается вертикальной прямой линией.
На рис. 1.5 приведена диаграмма Т, s для реального газа. На диаграмме нанесена сетка изобар, конфигурация которых аналогична конфигурации этих кривых на диаграмме Т, v (см. рис 1.2). На докритических изобарах левая ветвь кривой характеризует состояния жидкости, правая — перегретого пара, а горизонтальный участок изобары ––
Рис. 1.5. Диаграмма T, s для реального газа.
|
состояния влажного пара. Двухфазная область отделена от однофазной пограничной кривой, максимум которой соответствует критической точке К. Левая и правая ветви этой кривой на диаграмме Т, s примерно симметричны.
Критическая изобара касается пограничной кривой в критической точке, где имеет горизонтальную касательную и точку перегиба. Сверхкритические изобары представляют собой монотонные кривые, имеющие перегибы. В области жидкости изобары близки к пограничной кривой. По мере роста температуры и понижения давления конфигурация изобар в однофазной области приближается к конфигурации изобар идеального газа в этихкоординатах.
На диаграмме Т, s также наносят изохоры, которые круче изобар (как и для идеального газа). В двухфазной области изохоры — наклонные кривые малой кривизны, обращенные выпуклостью вверх. При переходе из однофазной области в двухфазную изохоры имеют излом, которому соответствует скачок изохорной теплоёмкости.
На диаграмме Т, s часто наносят линии h = const (изоэнтальпы). Они располагаются тем выше, чем больше значение энтальпии. С понижением давления эти линии стремятся к горизонталям, так как свойства пара приближаются к свойствам идеального газа. Некоторые изоэнтальпы имеют максимум, соответствующий точке на кривой инверсии. Эта кривая отделяет область параметров, в которой дроссельный эффект α h = (дТ/др) h положителен, от области, где α h <0. Положение кривой инверсии и упомянутых областей показано на диаграмме р,Т (рис. 1.6), а особенности процесса дросселирования рассматриваются в § 2.5.
Рис. 1.6. Кривая инверсии (1) и кривая парообразования (2): α h >0 – область понижения температуры газа при дросселировании, α h <0 – область повышения температуры газа.
|
Пользуясь формулой (1.24) для энтропии влажного пара, наносят в двухфазной области диаграммы T, s линии x =const (на рис. 1.5 они не нанесены). Предельным значениям х= 0 и х= 1соответствуют пограничные кривые жидкости и пара. Все линии х= сonst сходятся в критической точке.
На диаграмме Т, s площадь под кривой процесса изображает теплоту процесса, поэтому диаграмма называется тепловой. Площадь под участком изобары 1–2 соответствует теплоте, идущей на нагрев жидкости от температуры Т 1 до температуры насыщения Тs, площадь под участком 2–3 — теплоте парообразования, а площадь под участком 3–4 — теплоте перегрева пара от температуры насыщения до Т 4.
Диаграмма Т, s с сетками изобар, изохор и изоэнтальп называется полной, поскольку с её помощью можно выполнять расчеты, не привлекая уравнение состояния либо таблицы термодинамических свойств. Тем не менее, желательно помимо диаграммы использовать таблицы, так как значения удельного объёма и энтальпии определяются по ней с большой погрешностью, особенно в области жидкости.
Тепловая диаграмма удобна для анализа циклов, но для инженерных расчетов чаще применяют диаграмму h, s (рис. 1.7),с помощью которой значения энтальпии определяются проще и точнее. На диаграмме h, s критическая точка расположена не в максимуме пограничной кривой, а левее, так как энтальпия насыщенного пара достигает максимума при докритическом давлении (для водяного пара при р =3 МПа), а при дальнейшем росте давления убывает.
Рис. 1.7. Диаграмма h, s для реального газа
|
На диаграмме h, s нанесены изобары, изохоры, а также изотермы в области перегретого пара и линии x = const в области влажного пара, в которой изотермы совпадают с изобарами. Для влажного пара изобары — прямые линии, так как их тангенс угла наклона (∂ h /∂ s) p = T в этой области равен температуре насыщения Ts то есть постоянен для изобары.
Чем выше давление насыщения (а следовательно и температура насыщения), тем круче изобара в двухфазной области. Этим обусловлен веерообразный ход изобар в двухфазной области на диаграмме h, s. В отличие от диа грамм T, v и T, s, на диаграмме h, s изобары плавно переходят из двухфазной области в однофазную, так как в точке перехода для обоих участков изобары (∂ h /∂ s) p = Ts.
Из соотношения (∂ h /∂ s) p = T очевидно, что кривизна изобар на диаграмме h,s всегда положительна. Следовательно, все изобары, в том числе и сверхкритические, не имеют перегибов. Изохоры, как и на диаграмме T, s, имеют бὀльшую крутизну, чем изобары.Кривые х= сonst на диаграмме h, s рассчитывают и строят так же, как на диаграмме T, s.
Изотермы на диаграмме h, s с ростом энтропии (то есть с понижением давления) стремятся к горизонтальным прямым, соответствующим изотермам идеального газа. На ряде изотерм имеются минимумы, геометрическое место которых на этой диаграмме образует кривую инверсии.
При малых значениях x, а также при высоких давлениях и низких температурах изобары сближаются и примыкают к пограничной кривой жидкости. Поэтому диаграмма h, s обычно охватывает не всю двухфазную область, а лишь часть её при значениях x> 0,65.
На диаграмме h, s теплота изобарного процесса и техническая работа изоэнтропного процесса, равные разности значений энтальпии, изображаются отрезками (а не площадями, как на диаграмме Т, s). Это упрощает расчёты и обусловило широкое применение диаграммы h, s на практике.
При помощи диаграмм Т, s и h, s можно определять свойства перегретого пара и жидкости, если заданы значения давления и температуры, и свойства влажного пара, если известны значения степени сухости и давления (либо температуры). С помощью диаграммы h, s можно найти температуру насыщения пара по его давлению, определив, какой изотерме соответствует точка пересечения данной изобары с пограничной кривой. Хотя на диаграмме h, s пограничная кривая жидкости не представлена, для низких и умеренных давлений можно с приемлемой точностью определить значение энтальпии воды в состоянии насыщения, необходимое при расчётах циклов паротурбинных установок, по формуле
| (1.25) |
где ts,°С— температура насыщения при данном давлении,
размерность значения энтальпии — кДж/кг.
Коэффициент 4,1868 в формуле (1.25) представляет собой изобарную теплоёмкость воды в кДж/(кг.К), которую при невысоких давлениях можно считать постоянной. При давлении насыщения менее 3 МПа погрешность значений энтальпии, рассчитанных по (1.25), не превышает 3 %.
При расчётах циклов парокомпрессорных холодильных установок применяют специальную диаграмму h,ln p, а при расчетах процессов во влажном воздухе –– диаграмму H, d (энтальпия–влагосодержание). Диаграмма h,ln p рассматривается в курсе холодильных установок, а диаграмма H, d описана в последнем разделе данного пособия.
