Термодинамические процессы

В РЕАЛЬНОМ ГАЗЕ

При исследовании термодинамического процесса требуется определить значения всех параметров рабочего тела в начале и конце процесса, а также вычислить работу, совершенную телом, и подведенную к нему (либо отве­денную) теплоту. Для этого необходимо знать уравнение процесса в какой-либо системе координат, уравнение состояния рабочего тела и уравнение для расчета внутренней энергии. Также должны быть заданы параметры, опре­деляющие начальное состояние рабочего тела (например, Т и р для перегретого пара, р и х для влажного пара), и один из изменяющихся в процессе параметров в конечном состоянии (либо величина, по которой его можно рассчитать). Выбор тех или иных исходных данных обусловлен характером про­цесса либо решаемой задачей. Например, могут быть заданы параметры рабочего тела в одном из указанных состояний и значение теплоты либо работы процесса, а требуется оп­ределить параметры в другом состоянии.

Для воды и водяного пара и для многих хладагентов имеющиеся таблицы и диаграммы пол­ностью заменяют уравнение состояния и уравнение для внутрен­ней энергии и позволяют рассчитывать термодинамические процессы. При решении задач применение аналитического либо графического метода в конкретных случаях определяется видом процесса и требуемой точностью расчета. В принципе, все термодинамические задачи можно решить с помощью таб­лиц, однако тогда приходится много интерполировать. Поэтому иногда сочетают оба метода: часть свойств определяют по таблицам, а часть — по диаграммам.

Существенной особенностью процессов в любом реальном газе является возможность их протекания как в однофазной, так и в двухфазной области или последовательно в обеих фазах. Поэтому всегда необходимо определять с помо­щью таблиц либо диаграмм, к какой из этих областей относятся начальное и конечное состояния рабочего тела. Это обстоятельство определяет использование тех либо иных таблиц и, при необходимости, фор­мул для расчета свойств влажного пара.

При расчетах процессов могут встретиться следующие случаи:

1. Начальное и конечное состояния относятся к однофазной области, причем процесс может либо полностью протекать в этой области, либо проходить также через двухфазную область. В этом случае задача решается с помощью таблиц для жидкости и перегретого пара.

2. Начальная и конечная точки лежат в двухфазной области. В такой ситуации используют таблицы для кривой насыщения и формулы для расчета свойств влажного пара.

3. Процесс начинается в однофазной, а заканчивается в двухфазной области (либо наоборот). В данном случае термодинамические свойства в точке, относящейся к однофазной области, определяют по таблице свойств жидкости и перегретого пара, а свойства во второй точке рассчитывают по формулам для свойств влажного пара с использованием таблиц для состояния насыщения.

Во всех случаях задачи можно решать с помощью диаграмм, но следует иметь в виду, что на диаграмме h, s для водяного пара отсутствуют пограничная кривая насыщенной жидкости и область жидкости.

Ниже рассматриваются процессы, протекающие при постоянных значениях тер­мических параметров (изобарный, изохорный и изотермический), а затем более сложные процессы, совершающиеся при постоян­ных значениях калорических свойств (адиабатный (изоэнтропный) и процесс дросселирования). В заключение главы подробно рассмотрен весьма важный для паротурбинных установок процесс течения пара.

2.1. Изобарный процесс

Данный процесс весьма распространен на практике и имеет место в боль­шинстве теплообменных аппаратов. В частности, процесс нагрева жидкости до температуры кипения, парообразования и перегрева пара в котельном агрега­те протекает при постоянном давлении.

Для изобарного процесса деформационная работа (работа рас­ширения) рассчитывается по формуле

(2.1)

а техническая работа равна нулю (поскольку при p = const dp =0)

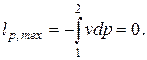
(2.2)

Из второй формы основного уравнения термодинамики

(2.3)

следует, что в изобарном процессе теплота q_p равна изменению энтальпии (так как l_{p , тех} =0). Изменение внутренней энергии ∆ и=и ₂ —и ₁определяется из первой формы основного уравнения термодинамики.

(2.4)

Приведенные формулы справедливы независимо от области проте­кания процесса. Если в процессе участвуют М кг вещества, в фор­мулах появляется множитель М.

Рис. 2.1. Изобарный процесс в реальном газе на диаграммах T, s и h, s.

На рис. 2.1. изображены три отмеченных выше случая протекания изобарного процесса. В первом случае, когда начало и конец про­цесса относятся к однофазной области (например, в процессах 1–2, 3–4, 5–6, 3–6), следует задать давление р, начальную и ко­нечную температуры Т ₁и Т ₂. Тогда по таблице для однофазной области (либо по диаграм­мам) находят значения v ₁, h ₁, v ₂, h ₂и рассчитывают значения энергетических эффектов (l, q и Δ u) по соотношениям (2.1), (2.3) и (2.4).

Во втором случае, когда процесс полностью протекает в двух­фазной области (например, процесс 7–8), задают давление р и значения степени сухости в начале и в конце процесса х ₁и х ₂. Значения v₁, v₂, h₁ и h₂ рассчитывают по формулам (1.22) и (1.23), причем значе­ния v', v ", h' и h" при заданном р берут из таблицы для состояния насыщения. Значения l, q и Δ u рассчитывают так же, как и в предыдущем случае.

Если процесс частично протекает в однофазной и частично в двухфазной области (процесс 4–7), для состояния, относящегося к однофазной области, помимо давления задают температуру, а для влажного пара — значение х. Значения v и h для первого состояния определяют по таблице, a для второго — по формулам (1.22) и (1.23). Затем рас­считывают значения l, q и ∆ и.

Могут встретиться и более сложные случаи задания параметров, когда вместо температуры либо степени сухости задано значение v, h либо s. Тогда состояние, в котором находится вещество, определяется путём сравнения заданного зна­чения свойства с его значениями в состоянии насыще­ния. Если состояние относится к однофазной области, то значения других свойств находят по соответствующей таблице линейной интерполяцией, если же к двухфазной, то вначале определяют степень сухости х,а затем рассчитывают значения других свойств по формулам для влажного пара. Определив зна­чения термических и калорических свойств в начале и в конце про­цесса, рассчитывают l, q и ∆ u.

 

2.2. Изохорный процесс

 

Этот процесс протекает при нагреве (охлаждении) газа в баллонах. Близок к изохорному процесс сжатия жидкости в насосах (например, воды при подаче её в котёл) ввиду малой сжимаемости жидкости.

Независимо от области, в которой протекает этот процесс, его деформационная работа равна нулю (так как при v = const dv =0)

(2.5)

а техническая работа рассчитывается по формуле

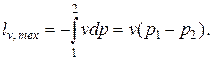
(2.6)

Из первой формы основного уравнения термодинамики (2.4) сле­дует, что в изохорном процессе теплота q_v равна изменению внут­ренней энергии (поскольку l_v =0).

При расчетах могут встретиться такие же случаи (рис. 2.2), как и рассмотренные выше при анализе изобарного про­цесса.

Рис. 2.2. Изохорный процесс в реальном газе на диаграммах T, s и h, s.

1. Если начальная и конечная точки процесса относятся к однофазной области (например, процессы 1–2, 3–4, 5–6 и 3–6), то помимо значения v следует задать значения давления либо температуры в этих точках. По указанным данным с помощью таблицы определяют интерполяцией значения третьего термиче­ского параметра и калорических свойств в начале и конце процесса. Затем рассчитывают значения внутренней энергии u ₁ =h ₁– p ₁ v и u ₂ =h ₂– p ₂ v и теплоты процесса q_v=u ₂ –и ₁.

2. В том случае, когда процесс протекает только в двухфазной обла­сти (например, процесс 7–8), начальное и конечное состояния могут быть заданы так же, как и в предыдущем случае. Тогда по значениям p ₁ и р ₂(либо Т ₁ и Т ₂ ) с помощью таблицы для состояния насыщения находят значения v ₁ ', v ₁ ", h ₁ ', h ₁ " и v ₂ ', v ₂ ", h ₂ ', h ₂ ". Используя задан­ное значение v, рассчитывают х ₁ и х ₂ из соотношения (1.22), а затем значения h ₁ и h ₂ по формуле (1.23). Располагая значения­ми р, v и h в начальном и конечном состояниях, можно определить u ₁, и ₂и q_v.

Иногда могут быть заданы значения v, x ₁и x ₂. Тогда опреде­ляют приближенные значения удельного объёма насыщенного пара v ₁ " = v/x ₁и v₂" = v/x ₂и по таблице для состояния насыщения находят соответ­ствующие значения Т ₁, Т ₂либо р ₁, р ₂. Затем на основании форму­лы (1.22) уточняют значения температуры либо давления насы­щенного пара методом последовательных приближений до приемлемого согласования заданного и расчетного значений v, после чего рассчитывают значения h ₁, h ₂, u ₁, и ₂и q_v. С помощью диаграмм такая задача решается без приближений, но на диаграмме h, s большая часть двухфазной области не представлена.

3. Если процесс протекает частично в однофаз­ной, а частично в двухфазной области (например, процессы 4–7, 5–8), для начального и конечного состояний помимо величины v должны быть заданы значения температуры (либо давления). Для влажного пара можно задать значения v и х. Тогда определяют энтальпиюв этих состояниях с помощью соответствующих таблиц, а затем рассчитывают значения u ₁, и ₂и q_v.

Когда заданное значение температуры либо давления меньше критического, для определения области состояний, к которой от­носится точка, следует сравнить значение v с величинами v' и v", найденными по таблице для кривой насыщения. Если v<v', точка относится к об­ласти жидкости, если v'<v<v" — к двухфазной области, при v>v" — к области перегретого пара.

2.3. Изотермический процесс

Этот процесс с реальным газом в однофазной области встреча­ется редко, но в двухфазной области изобарные процессы парообразования и конденсации одновременно являют­ся изотермическими.

Количество теплоты, подведенной к 1 кг вещества в изотерми­ческом процессе, рассчитывают по формуле

(2.7)

Деформационную и техническую работу изотермического про­цесса можно рассчитать по выражениям, полученным из основного уравнения термодинамики:

,	(2.8)
.	(2.9)

Следует подчеркнуть, что для реального газа, в отличие от идеального, значения разностей u ₂ – u ₁ и h ₂ – h ₁ на изотерме не равны нулю.

При расчетах могут встретиться те же случаи, что и при рассмотрении изобарного и изохорного процессов (рис. 2.3).

Рис. 2.3. Процесс T = const в реальном газе на диаграммах T, s и h, s.

1. Начало и конец процесса расположены в однофазной обла­сти (например, процессы 1–2, 3–4, 5–6, 3–6). В этом случае помимо температуры обычно задают начальное и конечное давле­ния р ₁и p ₂.Тогда по таблице находят значения v ₁, h ₁, s ₁ и v ₂, h ₂, s ₂, рассчитывают величины u ₁ и u ₂, а затем вычисляют q_Т, l_T и l_{T , тех} по формулам (2.7) – (2.9). Если вместо одного либо обоих значений давления заданы зна­чения удельного объёма, остальные свойства определяют по таблице интерполяцией.

2. Процесс протекает в двухфазной области (процесс 7–8). В этом случае изотермический процесс совпадает с рассмотренным выше изобарным процессом.

3.Процесс начинается в однофазной, а заканчивается в двухфазной области — процесс 4–7 (либо наоборот — процесс 8–5). Тогда для состояния, относящегося к однофазной области, помимо температуры задают давление, а для влажного пара — зна­чение х. Значения v и h для однофазного состояния определяют по соответствующей таблице, а для двухфазного рассчитывают по формулам (1.22) и (1.23), определив предварительно значения свойств пара и жидкости на пограничной кривой по таблице для состояния насыщения.

При расчетах изотермического процесса, так же как изобарного и изохорного, можно использовать диаграммы Т, s и h, s (исключительно либо в соче­тании с таблицами).

2.4. Изоэнтропный процесс

Этот процесс всегда встречается при тепловых расчетах циклов энергетических и холодильных установок, так как является идеальным (образцовым) процессом расширения водяного пара в турбине или сжатия хладагента в компрессоре холодильной установки.

Уравнение изоэнтропного процесса имеет вид s = сonst, отсюда следует, что он протекает без теплообмена между системой и окру­жающей средой, то есть является адиабатным. Действительно, поскольку ds = 0, теплота процесса также равна нулю

.

(2.10)

Из основного уравнения термодинамики в первой (2.4) и второй (2.3) формах при q = 0получаем

,	(2.11)
.	(2.12)

Итак, деформационная работа изоэнтропного процесса равна раз­ности значений внутренней энергии, а техническая — разности значений энтальпии в начальном и конечном состояниях.

Расчеты изоэнтропного процесса легче проводить с помо­щью энтропийных диаграмм h, s либо Т, s. При этом, как и для других процессов, могут встретиться следующие частные случаи (рис. 2.4):

1. Процесс полностью протекает в однофазной области (про­цесс 1–2). Тогда для начальной точки задают обычно температу­ру Т ₁ и давление p ₁, а для конечной — давление р ₂. Определив на диаграмме точку пересечения изотермы Т ₁и изобары р ₁,находят значения v ₁, h ₁ и s ₁. Из этой точки проводят изоэнтропу до пересечения с изобарой р ₂и, опре­делив конечное состояние, находят значения v ₂и h ₂. Затем определяют техническую работу по формуле (2.12) и дефор­мационную — по формуле (2.11), рассчитав предварительно зна­чения u ₁и u ₂.

При решении этой задачи с помощью таблиц определяют по таблице для однофазной области значения v ₁, h ₁ и s ₁. Если s ₁ >s ₂ " (где s ₂ " —

Рис. 2.4. Процесс s = const в реальном газе на диаграммах T, s и h, s.

значение энтропии насыщенного пара при давлении р ₂),то пар в конечном состоянии перегрет. Тогда по этой же таблице на изобаре р ₂линейной интер­поляцией находят точку, в которой s ₂ =s ₁, и определяют значения v ₂и h ₂в этой точке. Деформационную и техническую работу опре­деляют так же, как и при расчетах по диаграмме.

2. Процесс полностью протекает в двухфазной области (процесс 3-4). В этом случае задают давление р ₁(либо температуру Т ₁ ) и степень сухости х ₁в начале процесса (вместо х ₁ можно задать любое из аддитивных свойств — v ₁, h ₁ либо s ₁). Также задают давление в конце процесса р ₂.Определив начальную точку на пе­ресечении соответствующих кривых, находят значения неизвест­ных свойств в начальном состоянии, затем проводят из нее изоэнтропу до пересечения с изобарой р ₂и находят свойства в конечном состоянии. После этого можно рассчитать де­формационную и техническую работу по формулам (2.11) и (2.12).

Решая эту задачу с помощью таблиц, вначале определяют значения v’, v", h ', h", s' и s" при давлении р ₁(либо при температуре Т ₁) по таблицам для кривой насыщения. Зная значение х ₁,по формулам (1.22)–(1.24) рассчитывают значения v ₁, h ₁и s ₁. Если вместо х ₁задано одно из этих свойств, то сначала определяют х ₁ по соответствующей формуле, а затем рассчитыва­ют другие свойства. Поскольку в этом процессе s ₂ =s ₁, определив по таблице зна­чения s₂' и s ₂ " при давлении р ₂, рассчитывают степень сухости х ₂в конце процесса. Рассчитав затем значения v ₂и h ₂,получают все данные, необходимые для расчета l и l _тех.

3. Если начальная точка процесса расположена в однофазной области, а конечная — в двухфазной (процесс 5–6), значения свойств в начальном состоянии определяют так же, как в первом случае, а в конечном — так же, как во втором.

В процессе изоэнтропного расширения давление пара понижа­ется, поэтому если начальная точка процесса находится в одно­фазной области, то конечная может попасть в двухфазную. Если же начало процесса расширения находится в двухфазной области, то он весь расположен в ней. При изоэнтропном сжа­тии давление пара растёт, поэтому наблюдается обратная картина: процесс, начавшийся в однофазной области, полностью располо­жен там, а начавшийся в двухфазной области может закончить­ся в однофазной.

 

2.5. Процесс дросселирования

 

Дросселированием называется термодинамический процесс не­равновесного перетекания газа либо жидкости от большего дав­ления к меньшему без совершения работы. Дросселирование, про­текающее без теплообмена с окружающей средой, называется адиабатным. Этот процесс происходит при большом местном со­противлении, когда можно пренебречь изменением кинетической энергии. Из основного уравнения термодинамики для потока

(2.13)

видно, что при адиабатном дросселировании h ₁ =h ₂,то есть начало и конец процесса находятся на линии h = const (на изоэнтальпе).

Из второго закона термодинамики следует, что во всяком необратимом процессе энтропия возрастает. Так как дросселирование является явно необратимым процессом, то на энтро­пийных диаграммах конечная точка процесса всегда лежит правее начальной (рис.2.5). Заметим, что этот процесс изображают на диаграммах штриховой линией, подчеркивая его необратимость.

Во всех случаях, когда процесс начинается правее максимума линии h = const на диаграмме Т, s либо правее минимума изотермы на диаграмме h, s (процесс 1–2) температура вещества при дрос­селировании понижается (дроссельный эффект a_h=(∂T/∂p)_h положителен). Если же процесс начинается и оканчивается левее экстремумов этих линий (процесс 3–4), температура вещества повышается (дроссельный эффект отрицателен). Как отмечено в §1.3, кривая, соединяющая упомянутые экстремумы и разделяющая области параметров, в которых дроссельный эффект имеет разные знаки, называется кривой инверсии; на самой кривой a_h =0. Если процесс начинается в области a_h <0, а оканчивается в об-

Рис. 2.5. Процесс дросселирования реального газа на диаграммах T,s и h,s.

ласти a_h >0 (например, процесс 5–6), то в итоге может наблюдаться как пониже­ние, так и повышение температуры по сравнению с первоначальной в зависимости от соотношения протяженности участков процесса в соответствующих областях.

Для водяного пара в области параметров, охваченной диа­граммой h, s (до 800 °С и100 МПа), дроссельный эффект положи­телен. В области жидкости при температуре ниже 200°С дроссе­лирование воды сопровождается повышением температуры, и лишь при продолжении процесса в двухфазной области температура понижается.

В процессе дросселирования удельный объём реального газа во всех случаях увеличивается. При дросселировании влажного пара его степень су­хости чаще всего возрастает, но если начальная точка процес­са расположена на диаграмме h, s левее максимума соответствую­щей линии х = const, возможно некоторое уменьшение степени су­хости.

Рассматриваемый процесс играет особую роль в холодильной технике. При дросселировании холодильного агента его темпе­ратура понижается. Он поступает в испаритель при температуре, которая ниже температуры воздуха и продуктов, находящихся в охлаждаемом помещении. В испарителе влажный пар хладагента превращается в насыщенный пар, от­бирая при этом теплоту от охлаждаемого объекта.

Задачи, связанные с определением параметров пара после дросселирования, решают с помощью таблиц термодинами­ческих свойств либо диаграмм h, s и Т, s. При этом должно быть задано начальное состояние пара (значения р ₁, T₁ либо р ₁, х ₁) и конечное давление р ₂.

Решая задачи с помощью таблиц, по начальным парамет­рам определяют значение энтальпии h ₁ = h₂ и сравнивают его со значением энтальпии насыщенного пара h₂" при давлении р ₂. Если h₂<h ₂ ", то пар после дросселирования влаж­ный. Тогда по формуле (1.23) определяют значение х ₂, после чего, используя таблицу для кривой насыщения, можно рассчитать значения v ₂и s ₂по форму­лам (1.22) и (1.24). Если же h ₂ >h ₂ ", то пар в конце процесса перегрет, и его свойства определяют по таблице для однофазной области интерпо­ляцией на изобаре р ₂.

Проще всего решать задачи на процесс дросселирования с по­мощью диаграммы h, s. Определив начальную точку процесса как точку пересечения изобары p ₁с изотермой Т ₁(либо с кривой x ₁ = const), проводят через эту точку параллельно оси абсцисс линию h = const до пересечения с изобарой р ₂и таким образом определяют состояние пара в конце процесса.

 

2.6. Процесс течения

 

Процесс течения является основным рабочим процессом в паро­вой турбине, в которой пар под влиянием разности давлений с большой скоростью вытекает из сопел, попадает на лопатки рабочего колеса и отдает ему свою кинетическую энергию.

Расчет процесса течения газа (либо жидкости) заключается в определении скорости течения и двух каких-либо термодинамиче­ских свойств движущегося газа как функции пространственных координат. Другие характеристики движения могут быть вычис­лены по известным значениям этих трёх величин.

Ограничившись случаем, когда газ не совершает техническую работу (и к нему не подводится работа извне), запишем основное уравнение термодинамики для стационарного потока (2.13) в виде

(2.14)

откуда следует

(2.15)

Из уравнения (2.15) видно, что приращение кинетической энергии газа происхо­дит за счет уменьшения его энтальпии и подвода теплоты.

При непрерывном течении каждый элемент потока находится термодинамическом равновесии и имеет определенные значения параметров состояния, непрерывно изменяющиеся во времени и в пространстве. Таким образом, элемент потока при движении со­вершает термодинамический процесс, который аналогичен стати­ческому процессу. Однако в статическом процессе параметры рабочего тела из­меняются одновременно во всех его частях, а при течении процесс происходит последовательно во времени с каждым элементом. Оба процесса могут быть описаны одним и тем же уравнением, вид которого определяется только внешними воздействиями, оказы­ваемыми на поток — подводом теплоты и перепадом давлений в канале.

Для наблюдателя, перемещающегося вместе с потоком, основ­ное уравнение термодинамики записывается в виде (2.3):

.

На основании этого уравнения и (2.15) получим

(2.16)

то есть изменение кинетической энергии потока равно техниче­ской работе статического процесса, уравнение которого совпадает с уравнением процесса, совершаемого элементом потока. Если известно это уравнение в координатах р, v,можно рассчитать изменение кинетической энергии по формуле (2.16). Определив затем по параметрам начального и конечного состояний значения энтальпии h ₁и h ₂, можно вычислить количество теплоты, подве­денной к потоку, по уравнению (2.14).

Уравнения (2.13)–(2.15) справедливы как при наличии, так и при отсутствии в потоке трения, обусловленного силами вязкости, поскольку закон сохранения энергии, на основании которого полу­чено уравнение (2.13), справедлив для любых процессов. Для ря­да технически важных задач представляет интерес течение без трения и теплообмена (обратимое или идеальное адиабатное те­чение). Такой процесс является изоэнтропным, и для него спра­ведливо равенство

(2.17)

Из (2.17) следует, что при обратимом адиабатном течении скорость потока на выходе из канала равна

(2.18)

При истечении газа из сосуда большого объёма начальное значение скорости невелико и им можно пренебречь. В этом случае

(2.19)

где размерность w – м/с, h – Дж/кг.

Если значения h выразить в кДж/кг, формула (2.19) принимает вид

(2.20)

Значение разности энтальпий h ₁ – h ₂для любого реального газа, в том числе и для водяного пара, можно легко определить по диаграмме h, s,проведя линию s = const из начальной точки до пересечения с изобарой, соответствующей конечному давлению р ₂(рис. 2.6).

Для идеального газа можно подставить в формулу (2.19) вместо разности энтальпий известное выражение для технической работы изоэнтропного процесса. Тогда формула для скорости обратимого адиабатного течения идеального газа (при условии w ₁=0) примет вид

(2.21)

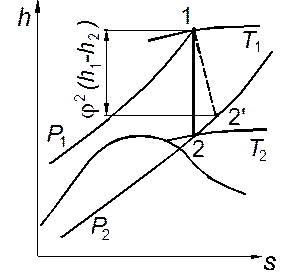Рис. 2.6. Процесс течения реального газа на диаграмме h, s.

На практике имеет место реальное (необратимое) адиабатное течение при наличии трения. Если сопоставить между собой ре­альный и идеальный процессы течения при одинаковых условиях, то сум­ма, фигурирующая в правой части уравнения (2.14), будет одной и той же в обоих случаях, но значения слагаемых будут разными. При трении часть кинетической энергии потока превращается в теплоту, которая воспринимается им и вызывает рост энтальпии, поэтому конечная скорость окажется меньше, а конечное значение энтальпии больше, чем в идеальном случае.

Реальная скорость потока w _2Допределяется через скорость иде­ального течения по формуле

,

(2.22)

где φ – скоростной коэффициент.

Значение φ, определяемое по опытным данным, меньше 1 и зависит от рода текущего вещества, состояния поверхности канала и других факторов. Для сопл паровых турбин, имеющих достаточно гладкую поверхность, значение φ находится в пределах 0,95–0,98.

Поскольку трение приводит к изменению энтальпии и других параметров потока, можно условно изображать необрати­мое адиабатное течение на термодинамических диаграммах, полагая, что теплота трения подводится извне. Этот процесс, сопровождающийся ростом энтропии, на энтропийных диаграммах расположен правее линии s = const, проведенной из начальной точки. На основании формул (2.19) и (2.22) получим

(2.23)

где h _2Д >h ₂ –– действительное значение энтальпии потока при заданном ко­нечном давлении р ₂.

Из уравнения (2.23) вытекает формула для определения величины h _2Д

(2.24)

где ξ = 1–φ² — коэффициент потери энергии.

Следовательно, если на диаграмме h, s от начальной точки изоэнтропы отложить вниз отрезок φ²(h ₁— h ₂ ) либо от конечной точки отложить вверх отрезок ξ(h ₁— h₂) и из его конца провести горизонтальную прямую до пересечения с изобарой р ₂, то точка пересечения 2' будет соответствовать реальному конечному со­стоянию потока вещества. Таким путём можно определить ряд промежу­точных состояний при различных давлениях и построить кривую реального процесса (изображенную штриховой линией на рис. 2.6).

Определив по диаграмме h, s значения температуры и энтро­пии в ряде промежуточных точек реального процесса, можно построить его на диаграмме Т, s (рис.2.7). На этой диаграмме изменение энталь­пии изображается площадью под изобарой. Так как при умерен­ных давлениях изобары в области жидкости практически совпада­ют с пограничной кривой, приращение кинетической энергии пото­ка при идеальном адиабатном течении, равное h ₁– h ₂, изобразится площадью 1–2–3–4, ограниченной двумя крайними изобарами, изоэнтропой и пограничной кривой жидкости. Площадь а–2–2'–b изобра­жает разность энтальпий в конце реального и идеального процес­сов h _2Д– h ₂, соответствующую потере кинетической энергии вслед­ствие трения. Площадь а–1–2'–b под кривой реального процесса соответствует теплоте, эквивалентной работе тре- ния. Из диаграммы Т, s видно, что потеря кинетической энергии меньше

работы трения. Это объясняется тем, что работа трения превращается в теплоту, которая воспринимается потоком и на последующих этапах про­цесса восстанавливает часть потерянной кинетической энергии.

Если бы процесс 1–2' протекал обратимо с подводом теплоты от внешнего источника, то в соответствии с уравнением (2.15) при­ращение кинетической энергии потока изображалось бы площадью 1–2'–2–3–4, то есть было бы больше, чем при реальном и даже при идеальном адиабатном течении. Следовательно, внутренний под­вод к потоку теплоты трения не эквивалентен подводу того же ко­личества теплоты извне.

Для определения профиля канала, по которому движется поток, необходимо рассмотреть вопрос о форме струи газа при его течении. Из уравнения (2.1) получим уравнение для приращения кинетической энергии потока в дифференциальной форме

(2.25)

Для изоэнтропного процесса уравнение (2.25) можно записать в виде

(2.26)

Рис. 2.7. Процесс действительного течения пара на диаграмме Т, s.

Производная (∂p/∂v)_s связана со скоростью распространения зву­ка а соотношением

(2.27)

Учитывая (2.27), представим уравнение (2.26) в виде

(2.28)

Для стационарного потока справедливо уравнение сплошности

(2.29)

где т — массовый расход,

f –– площадь поперечного сечения.

После логарифмирования и дифференцирования уравнения сплошности получим

(2.30)

Выразив из (2.28) величину dv / v и подставив ее в (2.30), получим окончательно

(2.31)

где M = w / a –– так называемое число Маха (отношение скорости течения потока к местной скорости звука).

Уравнение (2.31) связывает изменение площади поперечного сечения струи при идеальном адиабатном течении без совершения технической работы с изменением скорости потока и с числом Маха. Анализируя это уравнение, рассмотрим сначала случай, когда скорость потока надо увеличить (dw> 0). Число Маха при этом условии возрастает, так как при изоэнтропном расширении давление и температура газа понижаются и скорость звука уменьшается. Тогда из (2.31) следует, что при M <1 df< 0, а при M> 1 df> 0. Следо­вательно, при ускоренном движении потока, имеющего дозвуковую скорость и достигающего при движении сверхзвуковой, струя газа вначале сужается, а затем расширяется. В минимальном (переходном) сечении при df = 0 M= 1, то есть скорость течения потока равна скорости распространения звука в нём. Профиль канала, по которому движется газ, во избежание по­терь кинетической энергии должен соответствовать рассмотренной форме струи.

Скорость звука в жидкостях существенно больше, чем в газах, поэтому течение жидкостей всегда происходит при дозвуковых скоростях (М <1), и для ускорения движения жидкости сечение канала должно уменьшаться (df< 0 ).

В так называемом струйном компрессоре или эжекторе наряду с ускоренным течением имеет место замедленное (диффузорное) течение, при котором кинетическая энергия струи переходит в по­тенциальную и давление потока в направлении движения возра­стает. При замедленном течении dw< 0 ииз уравнения (2.31)видно, что при М> 1 df< 0, а при M< 1 df> 0. Таким образом, если течение потока начинается при сверхзвуковых скоростях и заканчи­вается при дозвуковых, канал должен иметь сначала сужающуюся часть, а затем расши­ряющуюся.

При адиабатном течении с трением описанная форма струи со­храняется, но в минимальном сечении скорость потока несколько отлича­ется от местной скорости звука. При ускоренном движении потока сече­ние, в котором М= 1, находится в расширяющейся части струи.

Скорость течения, совпадающая с местной скоростью звука, называется критической, а давление в соответствующем сечении — критическим давлением истечения р _к. Отношение величины р _к к давлению p ₁ заторможенного потока в начальном сечении, в котором можно пренебречь скоростью w ₁, называется критическим отноше­нием давлений β_к. Если отношение давления среды р_а,в которую происходит истечение, к давлению p ₁больше значения β_к, канал должен иметь только сужающуюся часть, в противном случае он имеет также расширяющуюся часть. Сопло, состоящее из сужаю­щейся и расширяющейся частей, впервые применил для получения сверхзвуковых скоростей течения газа шведский инженер Лаваль в конце XIX века.

Для изоэнтропного течения идеального газа критическое отно­шение давлений и критическую скорость течения можно определить аналитически. Сочетая уравнение для скорости течения идеального газа (2.21) с уравнением сплошности (2.29), получим следующее выражение для расчета площади поперечного сечения струи, соответствующего давлению р

(2.32)

Подставив в (2.32) выражение , получим

(2.33)

При заданных величинах p ₁ и v ₁ площадь поперечного сечения канала зависит только от отношения давлений p / p ₁= β, фигурирующего под корнем. Выражение в квадратных скобках обозначим через ψ

(2.34)

Из выражения для ψ видно, что оно дважды обращается в нуль: при β=0 и при β=1. Следовательно, функция ψ(β) имеет экстремум в интервале изменения β от 0 до 1. Взяв производную d ψ/ d β и приравняв её нулю, найдём то отношение давлений, при котором ψ имеет максимум, а значит, f имеет минимум. Это отношение давлений называется критическим и оказывается равным

(2.35)

Оно зависит от числа атомов в молекуле газа и равно 0,528 для двухатомного газа и 0,546 для трехатомного (при значении показателя адиабаты k = 1,3). Для водяного пара как реального газа величина β_к явля­ется переменной и зависит от начальных параметров потока, но в области перегретого пара при умеренных давлениях с приемле­мой точностью можно принимать значение β_к = 0,546, а для насы­щенного пара β_к = 0,577. При оценочных расчетах принимают β_к ≈ 0,5.

Подставив в формулу (2.21) выражение для β_к, определим критическую скорость течения идеального газа

(2.36)

Профилирование сопла заключается в определении зависимо­сти площади поперечного сечения от длины сопла. В простейшем случае расширяющаяся часть сопла имеет коническую форму с углом раствора γне более 12º (во из­бежание отрыва потока от стенок). Тогда достаточно определить диаметры минимального и выходного сечений d _minи d ₂,после чего можно рассчитать длину расширяющейся части l

(2.37)

Сужающуюся часть сопла чаще всего не рассчитывают, а профилируют так, чтобы сглаженный входной участок плавно сопрягался с минимальным сечением.

Площадь поперечного сечения определяют на основании урав­нения сплошности

(2.29a)

Значение скорости w вычисляют по формуле (2.20) для идеального течения либо по (2.22) для теченияс трением. Значения удельного объёма v во всех сечениях находят по диаграмме h, s либо по таблицам.

При известном значении р ₂ = р_а определение скорости и удель­ного объёма пара на выходе из сопла и расчет выходного сечения по уравнению (2.29а) не вызывает затруднений. Однако для водяного пара расчет давления p _кв минимальном сечении с учетом приведенных выше значений β_к носит приближенный ха­рактер, особенно при наличии трения. Поэтому для точного рас­чета сопла необходимо построить процесс течения на диаграмме h, s,определить значения w и v при промежуточных давлениях и рассчитать соответствующие значения f. Построив график зависимости f от р, можно найти минимальное сечение f _min,а затем вычислить значения d _min, d ₂и длину сопла. Для повышения точности опре­деления f _minцелесообразно при нахождении величин w и v ис­пользовать таблицы свойств и принимать меньший шаг по дав­лению в окрестности значения р _к,вычисленного по формуле p _к = p ₁β_к.

Если внешние условия изменяются по сравнению с теми, для которых рассчитано сопло, то некоторые характеристики процесса течения могут изменяться в определённых пределах. В качестве примера рассмотрим случай, когда имеется сужающе­еся сопло и уменьшается давление среды р_а, в которую происходит истечение,таким образом, что получается серия установившихся режимов течения при различных значениях р_а. Пока отношение p_a/p ₁превышает значение β_к, ско­рость на выходе возрастает и соответственно растет массовый расход пара т. При p_a/p ₁ = β_к в выходном сечении установятся кри­тическое давление истечения и критическая скорость и значение т станет максимальным. Дальнейшее уменьшение давления среды не изменит давление на выходе из сопла, скорость истечения и, следовательно, расход пара. Расширение пара за соплом от давления р ₂ = р _кдо давления р_а будет происходить неупорядочен­но и сопровождаться вихреобразованием, при котором кинетиче­ская энергия потока превращается в тепловую.

В случае истечения из отверстия в стенке резервуара либо из трубы постоянного сечения и при изменении давления среды скорость потока на выходе изменяет­ся таким же образом, как при истечении из сужающегося сопла. Однако тогда при любых значениях р_а возникают завих­рения потока перед входом в трубу и при выходе из неё, вызы­вающие потери энергии. Более подробно вопрос о течении газа при режиме, отличающемся от расчетного, рассмотрен в учебной ли­тературе.

Расчет процесса течения обычно выполняют, используя диаграм­му h, s. Здесь могут встретиться те же три частных случая, что и при расчете изоэнтропного процесса расширения (§ 2.4). Процесс идеального адиабатного течения, как изоэнтропный, изображается на этойдиаграмме линией s = сonst, а для построения реального про­цесса течения при наличии трения надо знать скоростной коэффи­циент φ и найти ряд промежуточных состояний. Заметим, что иногда идеальный процесс, начавшийся в однофазной области, может заканчиваться в двухфазной, а совершающийся в том же интервале давлений реальный процесс полностью расположен в однофазной области, так как конечные значения энтальпии и эн­тропии во втором случае больше, чем в первом (процессы 1–2 и и 1–2' на рис. 2.7). Определив по диаграмме значения разности энтальпий h ₁- h и удельного объёма для конечного и ряда проме­жуточных давлений, рассчитываем соответствующие значения w и f и находим размеры сопла по методике, изложенной выше.

Процесс течения, как и рассмотренные ранее процессы, может быть рассчитан с помощью таблиц термодинамических свойств, но этот способ является более трудоёмким, чем расчет по диаграмме h, s. Целесообразно основные расчеты выполнять по диаграмме, привлекая дополнительно таблицы для уточнения значений удель­ного объёма.