3.1. Параметрический способ задания кривой
Наиболее общим способом задания кривой является написание её уравнения в координатной или векторной формах (см. п.1.1.).
Координатная форма уравнения плоской кривой представляет собой систему
, (1)
где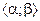 
, 
, – некоторый промежуток, а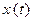 
и 
– определенные на нем функ- ции. Система (1) каждому t, 
сопоставляет точку плоскости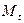 
с абсциссой 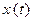и ординатой . Когда t, возрастая, пробегает отрезок 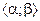, точка 
перемещается по плоскости; траектория, описываемая ею, и есть кривая G (рис.3.1).
Рис. 3.1.
Система
(2) есть координатная форма уравнения кривой G, расположенной в пространстве. Она каждому t, , ставит в соответствие точку 
, а кривая G есть траектория, которую описывает 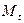, когда t, возрастая, пробегает отрезок 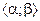(рис. 3.2). Уравнения 
, входящие в систему (2), называют параметрическими уравнениями кривой Г
Рис. 3.2.
Уравнение (1) плоской кривой можно считать частным случаем уравнения (2) при 
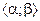на ; поэтому ниже, в основном, рассматриваем кривые, заданные уравнением (2). Это уравнение чаще записываем в векторной форме:
, (3)
где 
, 
. Заметим, что кривая G является годографом век- тор- функции
Ниже функции 
и 
, а, следовательно, и вектор- функцию 
, счи- таем непрерывными на .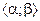
Пусть кривая Г задана уравнением (3).
Определение. Кривую Г назовём элементарной кривой, если из условия 
, следует 
.Уравнение кривой задает отображение отрезка 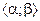числовой оси на множест- во точек плоскости или пространства, принадлежащих кривой. Это отображение непрерывно (так как непрерывная функция), а в случае элементарной кривой оно ещё и взаимно однозначно.
Рис. 3.3.
|
Пример 3. Пусть плоская кривая G является графиком функции 
, непрерывной на промежутке 
, 
: 
(рис.3.3). Уравнение этой кривой можно записать в явной форме 
; можно записать для нее параметрические уравнения:
.
Очевидно, график G есть элементарная кривая.
Определение. Точку P, 
, назовем кратной точкой кривой или точкой самопересечения, если существуют 
и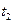 
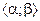, , принадлежащие и такие, что точки 
и 
совпадают с P (следовательно, 
).
Пример 1. Рассмотрим плоскую кривую G, заданную системой
.
Эта кривая изображена на рис.3.4. При возрастании t точка 
описывает G, двигаясь в направлении, указанном на рисунке стрелками. При 
она проходит через точку 
; описав петлю, она снова проходит через точку P при 
. P – точка самопересечения кривой G.
Рис. 3.4.
|
Кривая, имеющая хотя бы одну точку самопересечения, не является элементарной.
Замечание. Если хотя бы одна из координатных функци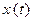й , и 
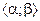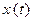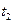строго монотонна на , то кривая G, заданная уравнением (3), является элементарной кривой. Дей- ствительно, пусть, к примеру, , строго моно- тонна. Тогда для любых и , , лежащих на 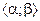, будет выполнено 
, а этого достаточно, чтобы утверждать: .
3.2. Касательная к кривой
В п.1.5. главы 2 было введено понятие о касательной к графику функции 
: касательная есть предельное положение секущей. Здесь мы определим это понятие для кривой, представленной параметрически и расположенной, вообще говоря, в пространстве.
Пусть G - элементарная кривая, заданная уравнением (3), где вектор- функция непрерывна на , .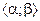
Зафиксируем некоторое число 
, 
, и определим для и 
вектор- функцию 
: 
Так как G – элементарная кривая, то при 
, поэтому определена при , причём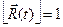 
(рис. 3.5.).
Допустим, что существует предел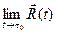 
; обозначим этот предел через 
. Обозначим также через 
точку с координатами 
, 
и 
(рис. 3.5).
Определение 2. Касательной к кривой G в точке назовем прямую 
, проходящую через точку параллельно вектору .
Замечание. Прямую 
, проходящую через точки и (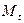
), , называют секущей. Вектор – направляющий вектор секущей (рис. 3.5). При 
секущая вращается вокруг точки так, что угол между 
и стремится к нулю. Имея в виду это обстоятельство, касательную называют предельным положением секущей 
при .
Определение 2 имеет смысл, если существует 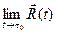. Между тем, этот предел существует не всегда.
Рис. 3.6.
|
Пример 1. Пусть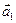 
, 
и 
– заданные векторы, причем 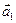и отличны от нуля и неколлинеарны. Обозначим через точку, радиусом-вектором которой является . Рассмотрим кривую G, уравнение которой
,
G состоит из двух лучей с общей вершиной : луча 
, параллельного 
и луча 
, параллельного (рис.3.6). При всех 
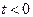точка 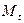лежит на , поэтому при 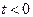вектор коллинеарен ; при 
коллинеарен . Отсюда ясно, что односторонние пределы в точке 
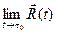различны, поэтому не существует. Следовательно, касательной к G в точке нет.
Итак, касательная существует не всегда.
Теорема 1. (О существовании касательной) Пусть вектор- функция в урав- нении (3) непрерывно дифференцируема в точке 
, 
, причём 
. Тог- да:
1) существует касательная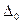 
к кривой G в точке 
, где , 
, 
;
2) уравнение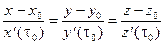 
, есть уравнение касательной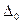
► Так как , то хотя бы одна из координат 
, 
, 
век- тора 
отлична от нуля. Для определенности будем считать, что 
. Функ- ция 
– непрерывна в точке , поэтому найдется 
такое, что на ин- тервале 
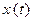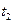. Значит, возрастает на этом интервале. Отсюда следует (см. замечание, п.3.1,): при любых и , , лежащих на интервале 
,справедливо .
1) В проколотой окрестности 
рассмотрим вектор- функцию :
Пусть 
. Имеем: 
.
Вектор-функция дифференцируема в точке , поэтому
;
отсюда: 
.
Итак, 
.
Аналогично получим:
.
Так как односторонние пределы одинаковы, то предел 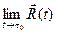существует и равен 
. Следовательно, касательная в точке Р0 существует: это прямая 
, проходящая через параллельно
2) Запишем каноническое уравнение прямой . Она проходит через точку , а вектор является её направляющим вектором. Очевидно, что векторы 
и 
сонаправлены; поэтому в качестве направляющего вектора прямой можно взять 
. Значит, каноническое уравнение запишется так: . 
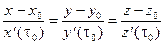Замечание. В процессе доказательства теоремы установлено, что вектор является направляющим вектором касательной . В этом состоит геометрический смысл производной вектор- функции..
Определение. Кривую G, заданную представлением (3), называют гладкой кри- вой, если
1) вектор-функция непрерывно дифференцируема на 
;
2) 
.
Из этого определения и доказанной теоремы вытекает, что в каждой точке глад- кой кривой существует касательная к ней. Кроме того, так как производная 
, определяющая направление касательной, непрерывна на , на кривой нет “угло- вых” точек - точек, при переходе через которые направление касательной меняется скачком. В этом состоит геометрический смысл определения гладкой кривой. Геометрически гладкая кривая – это кривая, имеющая в каждой точке касательную, положение которой при движении точки вдоль кривой изменяется плавно.
Определение. Плоскость, проходящую через точку , 
, перпендикулярно касательной 
к G в точке , называют нормальной плоскостью кривой G в точке . Всякую прямую, проходящую через перпендикулярно , называют нормалью кривой G в точке .
Если G задана представлением (3), то уравнение нормальной плоскости к G в точке 
запишется так:
.
Остановимся отдельно на случае, когда G есть плоская кривая, являющаяся графиком функции 
на промежутке 
, . Система
есть координатная форма уравнения Г, а
,
где 
, 
есть векторная форма её уравнения. Если имеет на непрерывную производную 
, то производная 
непрерывна и отлична от 
на ; поэтому Г удовлетворяет требованиям определения гладкой кривой.. Пусть 
, 
, где 
. Запишем уравнение касательной к G в точке 
(см. утверждение 2) теоремы):
, т.е.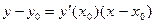 
(сравните с уравнением касательной, полученным в п.1.5. гл. 2).
3.3. Длина кривой
Пусть кривая G задана уравнением
, (3)
Рис. 3.8.
|
где вектор-функция 
непрерывна на 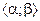, . Обозначим через T некоторый набор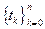 
чисел, лежащих на : 
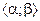. Введем также следующие обозначения: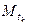 
– точка с координата- ми 
, 
, 
, 
; 
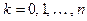– ломаная линия, звеньями которой являются прямолиней- ные отрезки 
, 
, 
, 
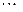. Вершины ло- маной , точки 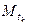, , 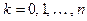лежат на G, мы будем говорить, что ломаная вписана в кривую G (рис.3.8). Через 
обозначим длину ломаной :
.
Определение 1. Длиной кривой G назовем точную верхнюю грань длин всевозможных ломаных, вписанных в G.
Обозначать длину G будем через 
. Таким образом, по определению
,
где 
есть совокупность всевозможных наборов чисел 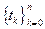таких, что ; здесь n принимает любые натуральные значения.
Величина – либо положительное число, либо 
. Достаточно ясно, напри- мер, что в такую неограниченную кривую, как парабола, можно вписать ломаную как угодно большой длины ; поэтому для параболы 
.
Определение. Кривую G назовем спрямляемой кривой, если ее длина есть неотрицательное число (т.е. если 
).
Введем обозначения, которые используются ниже. Пусть вектор-функция 
непрерывно дифференцируема на сегменте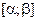 
Тогда функци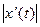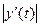и 
, 
и 
непрерывны, а потому и ограничены на 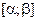. Обозначим через 
, 
и 
точные нижние грани на 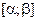функци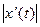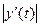й , и соотвеетст- венно, а через 
, 
и 
– точные верхние грани на 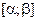этих функций.
Теорема 1. (Достаточный признак спрямляемости кривой) Пусть кривая G, задана уравнением (3), где непрерывно дифференцируема на сегменте 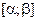. Тогда G спрямляема, а ее длина удовлетворяет неравенствам:
. (4)
Пусть 
, . Запишем выражение для длины ломаной , вписанной в кривую G:
.
По формуле конечных приращений (теорема 4, п. 2.2, гл. 2) на сегменте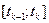 
найдутся точки 
, 
и 
такие, что 
, 
, 
, где 
. Отсюда:
. (5)
Так как 
, 
и 
, то
.
Неравенство 
справедливо для всякого набора T, поэтому
.
Тем самым доказаны спрямляемость кривой G и правая часть неравенств (4). Докажем левую часть этих неравенств. Из (5) имеем:
.
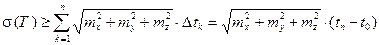Совокупность содержит всевозможные наборы ; среди этих наборов имеются такие, для которых 
и 
. Если набор удовлетворяет условиям и , то 
, поэтому и 
не меньше 
, т.е. 
.
3.4. Уравнение с натуральным параметром
Пусть G – спрямляемая кривая, заданная уравнением (3). где вектор-функция непрерывно дифференцируема на сегменте , .
Обозначим через 
длину дуги, ограниченной точками 
и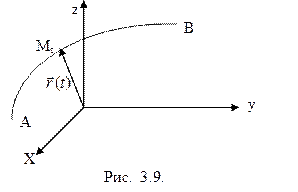 
(рис. 3.9). Величину будем рассматривать как функцию аргумента t, заданную на сегменте . Эту функцию называют переменной длиной дуги. Заметим: 
.
Теорема. (О переменной длине дуги) Переменная длина дуги 
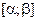дифференцируема на , причем 
.
Пусть 
, 
и такое, что 
. Обозначим: 
. 
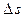есть длина дуги кривой G, которую пробегает точка 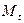при возрастании t от 
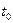до 
. По теореме о достаточном признаке спрямляемости
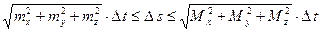, (6)
где 
, 
и – точные нижние грани 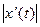, 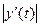и на 
, а , и – точные верхние грани на тех же функций. Так как указан- ные функции непрерывны на , существуют лежащие на точки 
, 
и 
, такие, что 
, 
, 
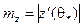, а также точки 
, 
, и 
, такие, что 
, 
, 
. Из (6) теперь получим:
.
При 
, каждая из точек 
стремится к 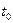справа, поэтому, так как , 
и 
непрерывны в точке 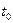, получим:
.
Здесь 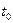– произвольное число из 
; значит, 
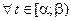
. (7)
Пусть теперь 
, 
и такое, что 
Заметим, что при приращение 
. Аналогично изложенному выше получим:
, (8)
где 
, 
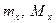и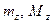 
– точные грани на 
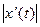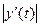функций , и соответственно. Поделив все части (8) на отрицательное число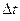 
, получим:
. (9)
На существуют точк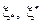и 
, 
и 
, в которых 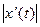, , 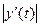достигает своих точных нижних и верхних граней. Из (9) имеем:
.
Перейдя здесь к пределу при 
, получим:
.
Здесь 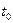– произвольное число из 
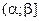; следовательно, доказано: 
. (10)
Из (7) и (10) вытекает: 
. Кроме того, 
(см. (7) и 
(см. 10)). Таким образом, утверждение теоремы справедливо.
Пусть кривая G, заданная представлением (3) является гладкой. Тогда . Но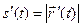 
; значит, 
на 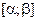, и функция 
возрастает на 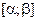от 
до 
. Обратная функция 
возрастает на 
, множество ее значений есть ;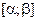 
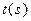дифференцируема на , причем 
(гл.2, п. 1.3.).
Обозначим: 
. Когда s возрастает от 0 до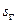 
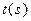, возрастает от a до b, так что годографом вектор- функции 
на является годограф вектор-функции на 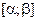, т.е. кривая G. Следовательно, G можно задать параметрически уравнением
, (11)
в котором параметр s имеет геометрический смысл длины дуги. Этот параметр называют натуральным параметром кривой G, а уравнение (11) – уравнением G с натуральным параметром (иногда – натуральным уравнением G).
Замечание. Вектор-функция 
в уравнении (11) непрерывно дифференцируе- ма на , причем 
.
Из (2) следует, что 
непрерывна и не обращается в нуль на 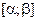; поэтому 
непрерывна на . Имеем:
.
