2.1. Производная вектор- функции в точке
Пусть вектор-функция  определена в окрестности
определена в окрестности  точки t0 , т.е. на не- котором интервале (α,β),
точки t0 , т.е. на не- котором интервале (α,β),  , и пусть t принадлежит этой окрестности, но не совпадает с t0. Составим проиэведение скалярного множителя
, и пусть t принадлежит этой окрестности, но не совпадает с t0. Составим проиэведение скалярного множителя 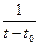 на вектор разности
на вектор разности  -
-  :
:  . Это произведение представляет собой вектор- функцию, определённую в проколотой окрестности точки t0 , и можно ставить вопрос о сущест- вовании её предела при
. Это произведение представляет собой вектор- функцию, определённую в проколотой окрестности точки t0 , и можно ставить вопрос о сущест- вовании её предела при  . В дальнейшем выражение
. В дальнейшем выражение  будем записывать в виде дроби:
будем записывать в виде дроби:  .
.
Определение. Если существует 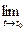
 , то этот вектор называют произ- водной вектор-функции
, то этот вектор называют произ- водной вектор-функции  в точке t0 .
в точке t0 .
Производную вектор-функции  в точке t0 обозначают символами
в точке t0 обозначают символами  и
и  . Таким образом,
. Таким образом,


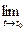

Используя введённые в п.3 обозначения, можем записать:


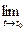
 =
= 
 =
= 
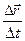 =
= 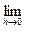
 .
.
Установим связь между производной вектор-функции и производными её координатных функций.
Теорема 7. ( О связи производной вектор- функции с производными её коорди- натных функций) Пусть вектор-функция  определена в окрестности
определена в окрестности  t0
t0  , а x (t), y (t) и z (t) – её координатные функции. Тогда:
, а x (t), y (t) и z (t) – её координатные функции. Тогда:
1) для того, чтобы существовала производная  необходимо и достаточно, чтобы существовали производные
необходимо и достаточно, чтобы существовали производные  и
и  ;
;
2) если производные  и
и  существуют, то
существуют, то
 =(
=( ,
,  )
)
► Так как  -
-  = (x (t)- x (t0), y(t)- y(t0), z (t) - z (t0)), то
= (x (t)- x (t0), y(t)- y(t0), z (t) - z (t0)), то

 =
=  .
.
1) Необходимость. Пусть  существует:
существует: 

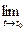
 . По тео- реме о покоординатной сходимости координаты вектора
. По тео- реме о покоординатной сходимости координаты вектора  являются пределами при
являются пределами при  соответствующих координатных функций
соответствующих координатных функций  ,
,  ,
,  вектор-функции
вектор-функции  . Значит, каждая из дробей
. Значит, каждая из дробей  ,
,  ,
,  имеет при
имеет при  конечный предел, т. е. производные
конечный предел, т. е. производные 
 и
и  существуют.
существуют.
Достаточность. Пусть существуют  и
и  , т.е. дроби
, т.е. дроби  ,
,  и
и  имеют при
имеют при  пределами числа
пределами числа 
 и
и  соответственно. Тогда из теоремы о покоординатной сходимости следует, что существует предел при
соответственно. Тогда из теоремы о покоординатной сходимости следует, что существует предел при  вектор-функции
вектор-функции  , причём числа
, причём числа  и
и  являются его координатами, т.е.
являются его координатами, т.е.  существует, причём
существует, причём
 =(
=( ,
,  ),
),
2) Это утверждение уже доказано, см. Достаточность. ◄
2.2.. Дифференцируемые вектор-функции
Пусть  - скалярная функция, определенная в окрестности
- скалярная функция, определенная в окрестности  . t0
. t0  , а μ – - некоторое положительное число. Если
, а μ – - некоторое положительное число. Если  , то говорят, что при
, то говорят, что при 
 есть “о малое” от
есть “о малое” от  и при этом записывают:
и при этом записывают:  =
= 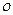 (
( ).
).
Сформулируем аналогичное понятие для вектор- функций.
Пусть вектор-функция  определена в окрестности
определена в окрестности  . t0
. t0  , а α1 (t), α2(t) и α3(t) – её координатные функции:
, а α1 (t), α2(t) и α3(t) – её координатные функции:  = (α1 (t), α2(t), α3(t)). Пусть, далее, μ – некоторое положительное число.
= (α1 (t), α2(t), α3(t)). Пусть, далее, μ – некоторое положительное число.
Определение. Если 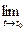
 , будем говорить, что при
, будем говорить, что при  вектор-функция
вектор-функция  есть “о малое” от
есть “о малое” от  и при этом записывать:
и при этом записывать:  =
= 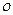 (
( ).
).
Замечание. Так как 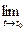

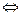
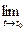
 (см. Замечание к теореме 1). а
(см. Замечание к теореме 1). а  - скалярная функция, то справедливо следующее утверждение: при
- скалярная функция, то справедливо следующее утверждение: при  вектор-функция
вектор-функция  есть “о малое” от
есть “о малое” от  тогда и только тогда, когда её длина
тогда и только тогда, когда её длина  при
при  есть “о малое” от
есть “о малое” от  .
.
Лемма. Чтобы при  вектор-функция
вектор-функция  была “о малым” от
была “о малым” от  , необходимо и достаточно, чтобы этим свойством обладала каждая её координатная функция:
, необходимо и достаточно, чтобы этим свойством обладала каждая её координатная функция:
 =
= 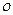 (
( )
) 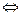
 .
.
► Имеем:  . По теореме о покоординат- ной сходимости
. По теореме о покоординат- ной сходимости
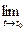

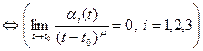 . ◄
. ◄
Определение. Вектор-функцию  назовём дифференцируемой в точке t0 , если она определена в некоторой окрестности этой точки, и существует вектор
назовём дифференцируемой в точке t0 , если она определена в некоторой окрестности этой точки, и существует вектор 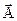 та- кой, что для приращения Δ
та- кой, что для приращения Δ  (h) справедливо асимптотическое представление:
(h) справедливо асимптотическое представление:
Δ  (h) =
(h) = 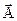 h +
h +  (3) Здесь
(3) Здесь  , Δ
, Δ  (h) =
(h) =  -
-  =
=  -
-  , а
, а  - некоторая вектор-функ- ция
- некоторая вектор-функ- ция  такая, что
такая, что 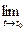
 .
.
Теорема 8. (Критерий дифференцируемости)Пусть вектор-функция  определена в окрестности
определена в окрестности  t0
t0  . Чтобы
. Чтобы  была дифференцируемой в точке t0 , необходимо и достаточно, чтобы существовала производная
была дифференцируемой в точке t0 , необходимо и достаточно, чтобы существовала производная  .
.
► Необходимость. Пусть  дифференцируема в точке t0. Заменив в форму- ле (3)
дифференцируема в точке t0. Заменив в форму- ле (3)  на
на 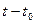 получим:
получим:  -
-  =
= 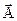
 + +
+ + 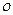 (
(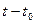 ). Отсюда:
). Отсюда:
 и
и 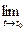
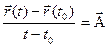 .+
.+ 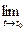
 . Так как
. Так как 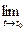
 =
=  , то
, то 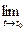
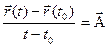 , т.е. производная
, т.е. производная  существует и равна
существует и равна 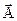 .
.
Достаточность. , Пусть  существует и пусть. x (t), y (t) и z (t) – координат- ные функции
существует и пусть. x (t), y (t) и z (t) – координат- ные функции  Тогда по теореме 6 существуют производные
Тогда по теореме 6 существуют производные  и
и  . Значит, эти скалярные функции дифференцируемы в точке t0; поэтому для их прира- щений справедливы представления:
. Значит, эти скалярные функции дифференцируемы в точке t0; поэтому для их прира- щений справедливы представления:


где  ,
,  ,
,  - функции, удовлетворяющие условиям:
- функции, удовлетворяющие условиям:

 Отсюда:
Отсюда:
 -
-  = (x (t0+h)- x (t0), y(t0+h)- y(t0), z (t0+h) - z (t0)) =
= (x (t0+h)- x (t0), y(t0+h)- y(t0), z (t0+h) - z (t0)) =
= (

 ) =
) =
= (

 ) h + h (
) h + h ( ,
,  ,
,  ) =
) =
=  h + h
h + h  ,
,
где  = (
= ( ,
,  ,
,  ). Ввиду условий, которым удовлетворяют
). Ввиду условий, которым удовлетворяют  ,
,  ,
,  , можем записать:
, можем записать:  . Итак,
. Итак,
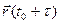 -
-  =
=  h + h
h + h  ,
,
где  . Заметим:
. Заметим: 
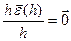 , т.е. h
, т.е. h  =
=  . Значит,
. Значит,
Δ  (τ) =
(τ) =  h +
h +  , (4) Получено представление (3), в котором
, (4) Получено представление (3), в котором 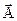 =
=  . ◄
. ◄
Следствие 1. Вектор 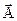 в представлении (3) приращения дифференцируемой функции определяется единственным образом, а именно,
в представлении (3) приращения дифференцируемой функции определяется единственным образом, а именно, 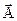 =
=  .
.
Этот результат уже получен, см. Необходимость.
Следствие 2. Если вектор-функция  дифференцируема в точке
дифференцируема в точке  , то суще- ствует вектор-функция
, то суще- ствует вектор-функция  , удовлетворяющая условиям
, удовлетворяющая условиям  , и такая, что справедливо представление Δ
, и такая, что справедливо представление Δ  (τ) =
(τ) =  h + h
h + h  .
.
Существование  уже доказано, см. Достаточность.
уже доказано, см. Достаточность.
Следствие 3. Вектор-функция  дифференцируема в точке
дифференцируема в точке  тогда и толь- ко тогда, когда в этой точке дифференцируемы её координатные функции.
тогда и толь- ко тогда, когда в этой точке дифференцируемы её координатные функции.
Утверждение следует из доказанной теоремы и теоремы 7.
Замечание. Если вектор-функция  дифференцируема в точке
дифференцируема в точке  ,то она и непрерывна в этой точке.
,то она и непрерывна в этой точке.
Действительно, из (3) следует:  ; значит (см. теорему 6),
; значит (см. теорему 6),  неп- рерывна в
неп- рерывна в  .
.
Пусть вектор- функции  и
и  , а также скалярная функция
, а также скалярная функция  определе- ны в окрестности
определе- ны в окрестности  точки t0 . Пусть, далее,
точки t0 . Пусть, далее,  -некоторое число, а
-некоторое число, а 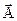 - некоторый вектор. Введём обозначения:
- некоторый вектор. Введём обозначения: 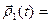
 +
+  ;
; 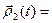

 ;
;  (
( ,
,  )- - скалярное произведение;
)- - скалярное произведение;  [
[  ,
,  ] - векторное произведение.
] - векторное произведение.
Теорема 9. (О действиях над дифференцируемыми вектор-функциями) Если  ,
,  и
и  дифференцируемы в точке t0 , то
дифференцируемы в точке t0 , то  ,
,  ,
,  и
и  также диф- ференцируемы в этой точке, причём
также диф- ференцируемы в этой точке, причём
1)  =
= 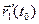 +
+  ;
;
2) 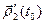 =
= 
 +
+ 
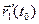 ; в частности, если
; в частности, если  ≡
≡  , то
, то 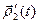 =
= 
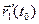 ;
;
3) 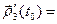 (
(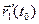 ,
,  ) + (
) + ( ,
,  ); в частности, если
); в частности, если  ≡
≡ 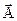 , то
, то 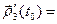 (
(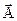 ,
,  ).
).
4) 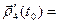 [
[ 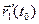 ,
,  ] + [
] + [ 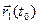 ,
,  ]; в частности, если
]; в частности, если  ≡
≡ 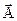 , то
, то  [
[ 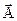 ,
,  ].
].
Доказательства всех четырёх утверждений проводятся по единой схеме. Из- ложим доказательство утверждения 4).
► Пусть 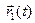
 ,
, 
 . Тогда
. Тогда  [
[  ,
,  ]=
]=  =
=
=  . По условию теоремы
. По условию теоремы  и
и  дифференцируемы в точке t0 ; значит (см. следствие 3 теоремы 8), в этой точке дифференцируемы их координатные функции. Отсюда вы-текает дифференцируемость в точке t0 функций
дифференцируемы в точке t0 ; значит (см. следствие 3 теоремы 8), в этой точке дифференцируемы их координатные функции. Отсюда вы-текает дифференцируемость в точке t0 функций  =
=  ,
,  = =
= =  и
и  =
=  , которые являются коорди- натными функциями вектор-функции
, которые являются коорди- натными функциями вектор-функции  . Следовательно (см. следствие 3 теоремы 8),
. Следовательно (см. следствие 3 теоремы 8),  дифференцируема в точке t0 . Значит, существует производная
дифференцируема в точке t0 . Значит, существует производная  , причём (см. теорему 7)
, причём (см. теорему 7)  = (
= ( ,
, 
 ). Вычислив производные
). Вычислив производные  ,
, 
 , получим:
, получим:
 =(
=(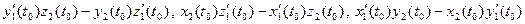 ) + (
) + ( ) = = [
) = = [ 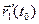 ,
,  ] + [
] + [ 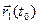 ,
,  ]. ◄
]. ◄
Теорема 10. (О производной сложной вектор-функции) Пусть скалярная функ- ция  определена в окрестности
определена в окрестности  , t0
, t0  , а вектор-функция
, а вектор-функция  определена в окрестности
определена в окрестности  точки
точки  =
=  . Если
. Если  дифференцируема в точке
дифференцируема в точке  , а
, а  дифференцируема в точке t0 , то сложная вектор-функция
дифференцируема в точке t0 , то сложная вектор-функция  дифференци- руема в точке t0 , причём
дифференци- руема в точке t0 , причём  .
.
► Пусть x (θ), y (θ) и z (θ) – координатные функции  :
:  = (x (θ), y (θ), z (θ)). Заметим:
= (x (θ), y (θ), z (θ)). Заметим:  =(
=( ). Так как
). Так как  дифференцируема в точке
дифференцируема в точке  , то в этой точке дифференцируемы её координатные функции (см. следствие 3 теоремы 8). По теореме о производной сложной скалярной функции суперпозиции
, то в этой точке дифференцируемы её координатные функции (см. следствие 3 теоремы 8). По теореме о производной сложной скалярной функции суперпозиции  дифференцируемы в точке t0 , причём
дифференцируемы в точке t0 , причём
 . Теперь можем записать:
. Теперь можем записать:
 (
( ) = (
) = ( ) =
) =
= ( =
=  . ◄
. ◄
Определение. Будем говорить, что вектор-функция  дифференцируема на интервале (α, β), если она дифференцируема в каждой его точке. Будем говорить, что вектор-функция
дифференцируема на интервале (α, β), если она дифференцируема в каждой его точке. Будем говорить, что вектор-функция  дифференцируема на сегменте [ α, β ], если она дифференцируе- ма на интервале (α, β) и, кроме того, существуют односторонние производные
дифференцируема на сегменте [ α, β ], если она дифференцируе- ма на интервале (α, β) и, кроме того, существуют односторонние производные


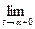
 и
и 

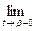
 .
.
Теорема 11. Пусть вектор-функция  непрерывна на сегменте [ α, β ] и диф- ференцируема на интервале (α, β). Тогда существует точка
непрерывна на сегменте [ α, β ] и диф- ференцируема на интервале (α, β). Тогда существует точка  (α, β) такая, что справедливо неравенство:
(α, β) такая, что справедливо неравенство:
 .
.
► Рассмотрим скалярную функцию f (t), заданную на [ α, β ] равенством: f (t) = ( ,
,  ). Из условия теоремы вытекает, что f (t) непрерывна на сегменте [ α, β ] и дифференцируема на интервале (α, β). По теореме Лагранжа существует точ- ка
). Из условия теоремы вытекает, что f (t) непрерывна на сегменте [ α, β ] и дифференцируема на интервале (α, β). По теореме Лагранжа существует точ- ка  (α, β) такая, что справедлива формула конечных приращений: f (β) - fα) = =
(α, β) такая, что справедлива формула конечных приращений: f (β) - fα) = =  . Отсюда: | f (β) - fα) | = |
. Отсюда: | f (β) - fα) | = |  . Опираясь на свойства скалярно- го произведения, можем записать:
. Опираясь на свойства скалярно- го произведения, можем записать:
f (β) – f(α) = ( ,
,  ) =
) =  ;
;
| 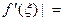 |((
|(( ,
,  )|
)| 
 | |
| |  |. Отсюда и из равенства | f (β) - fα) | = |
|. Отсюда и из равенства | f (β) - fα) | = |  следует:
следует:


 | |
| |  |
|  . Сократив на
. Сократив на 
 |, получим неравенство, которое и требовалось доказать. ◄
|, получим неравенство, которое и требовалось доказать. ◄
Теорема 12. Пусть вектор-функция  удовлетворяет на интервале (α, β) ус- ловию:
удовлетворяет на интервале (α, β) ус- ловию:  , где С≥ 0. Если
, где С≥ 0. Если  дифференцируема на интервале (α, β), то при всяком
дифференцируема на интервале (α, β), то при всяком  скалярное произведение (
скалярное произведение ( ,
,  ) равно нулю.
) равно нулю.
► Рассмотрим скалярную функцию f (t), заданную на (α, β) равенством: f (t) = ( ,
,  ) =
) =  . Очевидно, f (t)
. Очевидно, f (t)  на (α, β), и потому
на (α, β), и потому  на (α, β). Но
на (α, β). Но  (
( ,
,  ) = (
) = ( ,
,  ) + (
) + ( ,
,  )= 2 (
)= 2 ( ,
,  ). Отсюда:
). Отсюда:
( ,
,  )
)  на (α, β). ◄
на (α, β). ◄
Замечание. Если при соблюдении условий этой теоремы оба вектора  и
и  ненулевые, то они ортогональны.
ненулевые, то они ортогональны.
2.3. Дифференциал вектор- функции
Пусть вектор-функция  дифференцируема в точке t0 , t0
дифференцируема в точке t0 , t0  .
.
Определение. Дифференциалом вектор-функции  в точке t0 назовём произ- ведение
в точке t0 назовём произ- ведение  h, где h = Δ t – приращение аргумента t.
h, где h = Δ t – приращение аргумента t.
Обозначать дифференциал будем символами d  или d
или d  , подчеркнув во вто- ром символе то обстоятельство, что дифференциал представляет собой вектор-функ- цию аргумента h, определённую на всей числовой оси равенством d
, подчеркнув во вто- ром символе то обстоятельство, что дифференциал представляет собой вектор-функ- цию аргумента h, определённую на всей числовой оси равенством d  =
=  h или, так как приращение h = Δ t независимой переменной t равно дифференциалу d t, равенством d
h или, так как приращение h = Δ t независимой переменной t равно дифференциалу d t, равенством d  =
=  d t. Заметим ещё, что формулу (4) теперь можно записать в виде:
d t. Заметим ещё, что формулу (4) теперь можно записать в виде: 
Δ  (h) = d
(h) = d  +
+  .
.
Из утверждений теоремы 9 вытекают следующие правила вычисления диффе- ренциалов в точке  : Если
: Если 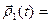
 +
+  ;
; 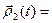

 ;
;  (
( ,
,  ) и
) и  [
[  ,
,  ], то
], то
1)  ;
;
2) 

 ;
;
3) 
 ;
;
4) 
 .
.
Иэ теоремы 10 вытекает инвариантность формы дифференциала вектор-функ- ции. Действительно, пусть  - скалярная функция, дифференцируемая в точке
- скалярная функция, дифференцируемая в точке  , а
, а  дифференцируема в точке t0 , где
дифференцируема в точке t0 , где 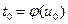 .Тогда сложная вектор-функ- ция
.Тогда сложная вектор-функ- ция  дифференцируема в точке
дифференцируема в точке  , причём
, причём 
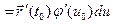 . Отсюда, так как
. Отсюда, так как  , получим:
, получим: 
 . Таким обра- зом, формула
. Таким обра- зом, формула 
 справедлива и в том случае, когда аргумент
справедлива и в том случае, когда аргумент  вектор-функ- ции
вектор-функ- ции  является зависимой переменной.
является зависимой переменной.
2.4. Производные и дифференциалы высших порядков
Пусть вектор-функция  дифференцируема в окрестности
дифференцируема в окрестности  точки
точки 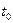 ,
,  , т.е. на некотором интервале
, т.е. на некотором интервале  ,
,  . Сопоставив каждому t,
. Сопоставив каждому t,  , вектор
, вектор  , мы определим на
, мы определим на  новую вектор-функцию, которую называют производной от вектор-функции
новую вектор-функцию, которую называют производной от вектор-функции  и обозначают через
и обозначают через  , или через
, или через  , или через
, или через  .
.
Если производная  дифференцируема в точке
дифференцируема в точке 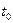 , то производную от
, то производную от  в точке
в точке 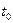 называют производной второго порядка от вектор-функции
называют производной второго порядка от вектор-функции  в точке
в точке 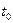 и обозначают через
и обозначают через  . Если производная
. Если производная  дифференцируема в каждой точке интервала
дифференцируема в каждой точке интервала  , то на
, то на  существует производная от вектор-функции
существует производная от вектор-функции  ; эту производную называют производной второго порядка от вектор-функции
; эту производную называют производной второго порядка от вектор-функции  и обозначают через
и обозначают через  , или через
, или через  , или через
, или через  . Вообще, при всяком натуральном n,
. Вообще, при всяком натуральном n,  , производной порядка n от вектор-функции
, производной порядка n от вектор-функции  называют производную от производной порядка
называют производную от производной порядка  этой вектор-функции, обозначая ее через
этой вектор-функции, обозначая ее через  , или через
, или через 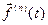 , или через
, или через  .
.
Определение 5. Будем говорить, что вектор-функция  n,
n,  , раз дифференцируема в точке
, раз дифференцируема в точке 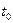 ,
,  , если в точке
, если в точке 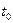 существуют производные от
существуют производные от  до порядка n включительно.
до порядка n включительно.
Для скалярных функций аналогичное понятие введено в §10 гл.1. Заметим, что n -кратная дифференцируемость вектор- функции  в точке
в точке 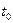 означает, что
означает, что  и ее производные
и ее производные  определены и дифференцируемы в некоторой окрестности
определены и дифференцируемы в некоторой окрестности  и, кроме того, производная
и, кроме того, производная  дифференцируема в точке
дифференцируема в точке 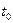 .
.
Упражнение. Доказать утверждения:
I. Пусть вектор-функция 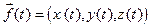 определена в некоторой окрестности
определена в некоторой окрестности  ,
,  . Тогда:
. Тогда:
1) ( n раз дифференцируема в точке
n раз дифференцируема в точке 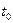 ) Û (
) Û (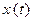 ,
,  и
и  n раз дифференцируемы в точке
n раз дифференцируемы в точке 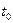 );
);
2) ( n раз дифференцируема в точке
n раз дифференцируема в точке 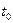 ) Þ
) Þ  .
.
II. Пусть вектор-функции  и
и 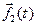 n раз дифференцируемы в точке
n раз дифференцируемы в точке 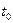 ,
,  , и пусть l – некоторое число, а
, и пусть l – некоторое число, а  – некоторый вектор. Положим:
– некоторый вектор. Положим:  ,
,  ,
, 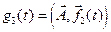 ,
,  . Тогда:
. Тогда:
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
В этом и предыдущих пунктах введены основные понятия дифференциального исчисления вектор-функций: предел, непрерывность, производная, дифференциал. Они аналогичны соответствующим понятиям дифференциального исчисления скалярных функций и обладают аналогичными свойствами. Однако, полной аналогии между тео- ремами дифференциального исчисления для скалярных и векторных функций нет. Например, ясно, что не имеет смысла говорить о наибольшем или наименьшем значе- нии вектор- функции на промежутке, поэтому для вектор- функции нельзя сформулиро-вать теорему, аналогичную теореме Ферма (гл.2, п.2.1.). Нет для вектор- функций и аналогов теорем Ролля, Коши и Лагранжа (гл.2, п. 2.2.). Однако, справедлива теорема, аналогичная теореме Тейлора- Пеано (§4).
Теорема 6. Пусть вектор-функция  n,
n,  , раз дифференцируема в точке
, раз дифференцируема в точке 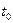 ,
,  . Тогда справедлива асимптотическая формула:
. Тогда справедлива асимптотическая формула:
 .
.
 Так как
Так как 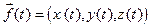 n раз дифференцируема в точке
n раз дифференцируема в точке 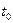 , то и ее координатные функции обладают этим свойством. По теореме Тейлора–Пеано (§4 гл.2)
, то и ее координатные функции обладают этим свойством. По теореме Тейлора–Пеано (§4 гл.2)
 ,
,
 ,
,
 ,
,
где  ,
,  ,
,  . Отсюда:
. Отсюда:
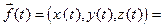

 ,
,
где  . Так как
. Так как  ,
,






