Вихревым движением называется вращательное движение частицы вокруг осей, проходящих через частицу.
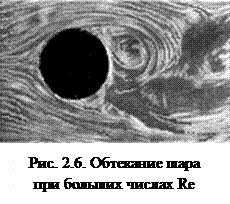Изучение вихревого движения жидкости и газа в аэродинамике имеет важное практическое значение. На вихревой теории, в частности, основаны методы определения аэродинамических характеристик крыльев бесконечного и конечного размаха. При обтекании тел реальным потоком может происходить отрыв потока с образованием вихрей (рис. 2.6).
Вращательное движение частиц характеризуется угловыми скоростями:
, 
,
.
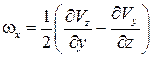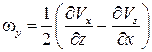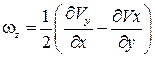То есть в каждой точке пространства вращение жидких частиц можно охарактеризовать вектором угловой скорости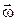 
, модуль которого равен 
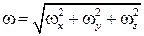. Каждый такой вектор 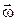характеризует местное вращение жидкости.
При исследовании полей угловых скоростей обычно вводят понятия, аналогичные тем, которые были введены применительно к полю линейных скоростей. Для описания поля угловых скоростей вращения вводится понятие вихревыхлиний. Построение вихревых линий аналогично построению линий тока (рис. 2.7).
Вихревой линией называется линия, проведенная в данный момент времени в потоке жидкости или газа, в каждой точке которой вектор угловой скорости направлен по касательной к ней.
По аналогии с линиями тока можно записать дифференциальные уравнения вихревых линий:
.
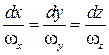Кроме понятия вихревых линий вводится понятие вихревых трубок. Рассмотрим произвольный малый замкнутый контур, не совпадающий с вихревой линией, и проведем через каждую точку этого контура вихревую линию (рис. 2.8). Совокупность этих линий образует вихревую трубку. Жидкость или газ, заключенные в ней, называются вихревым шнуром (вихревой нитью или вихрем).
Боковые поверхности вихревой трубки образованы вихревыми линиями, и, следовательно, поток вихря вектора скорости через боковую поверхность равен нулю.
Так как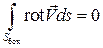 
, то поток вихря для любых поперечных сечений вихревой трубки (интенсивность вихря) одинаков: 
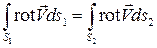. Если для поперечного сечения вихревой трубки 
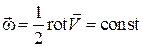, то интенсивность вихревой трубки постоянна:
.
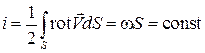Отсюда, вторая теорема Гельмгольца звучит следующим образом:
Поток вихря вектора скорости сквозь произвольно проведенное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки.
Из этой теоремы можно сделать вывод о возможных формах существования вихрей:
1. Сечение вихревой трубки нигде не равно 0, так как при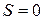 
и постоянной интенсивности вихревой трубки угловая скорость вращения 
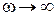, что физически невозможно.
2. Вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя (вихревые кольца), либо опираются на стенку (поверхность твердого тела) или на свободную поверхность (поверхность раздела двух сред с разной плотностью). Вихри теоретически могут иметь бесконечную протяженность, что возможно только в идеальной жидкости. В реальных условиях под действием сил вязкостного трения вихрь постепенно разрушается. Значение интенсивности (или напряжения) вихря связано с возникающей вокруг вихря циркуляцией вектора скорости.
При отсутствии вихревого движения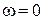 
. Если в этом случае траектории частиц представляют собой замкнутые кривые, то такое движение является частным случаем циркуляционного течения (частицы вращаются относительно оси, не проходящей через нее, и не вращаются относительно собственных осей).
В аэрогидромеханике важную роль играет понятие циркуляции скорости Г. Выделим в движущейся жидкости произвольный замкнутый контур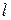 
(рис. 2.9). Пусть в некоторой точке этого контура скорость равна V, а проекция ее на касательную 
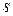к данной точке контура равна 
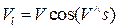. Запишем произведение 
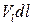и возьмем от него криволинейный интеграл по контуру :
.
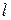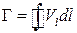Определяемая таким образом величина Г называется циркуляцией скорости по замкнутому контуру. При вычислении Г направление обхода контура (направление интегрирования) считается положительным, если охваченная контуром область остается слева.
Рассмотрим в качестве примера циркуляционного течения обтекание несимметричного профиля крыла плоскопараллельным потоком.
Допустим, что среда обтекает крыло, вызывая появление подъемной силы. Тогда скорости течения под нижней поверхностью крыла меньше скорости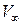 
невозмущенного набегающего потока, а над верхней поверхностью – больше 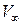. Характер возмущенного течения у крыла можно выяснить, вычитая из локальных скоростей скорости прямолинейного поступательного потока. В результате получим поток возмущения, т. е. движение, которое возникает в среде от присутствия крыла. Поскольку влияние 
крыла местное, то линии тока потока возмущения не уходят на бесконечность, а должны иметь начало и конец на поверхности крыла или быть замкнутыми. Такой поток с замкнутыми линиями тока и называют циркуляционным. Таким образом, течение у крыла можно представить как сумму поступательного невозмущенного потока и течения по замкнутым траекториям (рис. 2.10).
Интенсивность циркуляционного потока у крыла характеризуется величиной циркуляции скорости по замкнутому контуру :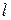
,
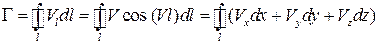где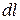 
– элемент дуги контура; 
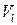– проекция скорости на элемент 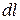. В общем случае произвольно выбранный контур 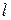может не совпадать с линией тока циркуляционного течения (рис. 2.11). Таким образом, циркуляционным называется движение, при котором циркуляция скорости 
; если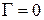 
, то движение среды происходит без циркуляции.
Если циркуляция скорости вокруг профиля (крыла) равна нулю, то профиль (крыло) не создает подъемной силы. Если величина подъемной силы не равна нулю, то в обязательном порядке около профиля создается циркуляционное течение и циркуляция скорости .
Применим понятие циркуляции скорости к сечению вихревой трубки, проведенному по нормали к ее оси. Вихревая нить индуцирует вокруг себя поле скоростей. При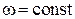 
скорость движения частиц на расстоянии 
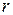от оси вихря определяется как 
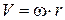. Выберем замкнутый контур, охватывающий вихрь, в виде окружности радиусом 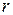. Тогда циркуляция вектора скорости по этому контуру будет равна 
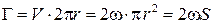, где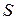 
– площадь, охватываемая окружностью. Полученное выражение есть не что иное, как удвоенная интенсивность вихревой трубки.
Таким образом, мы рассмотрели методы описания движения среды, математическое описание движения жидкой частицы, движения без вращения частицы, вихревого движения. Далее будут рассмотрены уравнения движения газа как сплошной среды.
Контрольные вопросы и задания
1. На основании анализа уравнения линии тока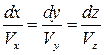 
покажите, что через критическую точку может проходить бесконечное число линий тока.
2. В некоторой точке пространства движущейся жидкости площадь поперечного сечения трубки тока становится равной нулю. Какой кинематический объект находится в этой точке пространства, если линии тока направлены в его сторону?
3. Почему через каждую точку потока можно провести только одну линию тока? Не находится ли данное положение в противоречии с кинематическим образом, о котором говорится в задании 2?
4. В чем принципиальное отличие движения жидкой частицы от движения твердого тела?
5. Потенциал скорости для некоторой точки пространства движущейся жидкости равен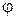 
. Запишите выражение для расчета величины скорости потока через потенциал.
6. Потенциал скорости в точке А равен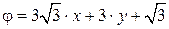 
(м2/с). Чему равны величина вектора скорости и угол его наклона к оси ОХ?
7. 
В некотором сечении площадью 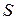вихревого жгута угловая скорость равна 
. Чему равна угловая скорость вращения вихревого жгута в сечении, площадь которого равна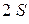 
?
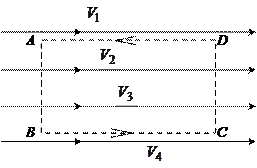
8. Рассчитайте величину циркуляции скорости Г по замкнутому контуру АВСD (рис. 2.12) при условии, что:
а) скорость течения во всем объеме движущейся жидкости одна и та же (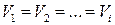
);
|
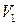на линии тока, прилегающей (совпадающей) с DA, равна 
.
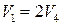В каком из вариантов наблюдается циркуляционное течение?
9. Объясните, почему на рис. 2.11 вектор скорости в нижней части контура обхода направлен именно таким образом.
10. 
Исходя из положения, что угловая скорость вращения не может быть равной ¥, объясните, что будет происходить с вихревым жгутом, образовавшимся в некотором месте пространства, и как он может себя вести.
