Задача кинематического изучения движения жидкости заключается в определении в каждой точке движущегося газа значения скорости для любого момента времени.
Движение газа можно изучать двумя методами – методом Эйлера или методом Лагранжа.
Метод Эйлера. В методе Эйлера фиксируется точка пространства с координатами x, y, z и исследуется изменение скорости частиц в этой точке с течением времени. Отслеживаемая скорость частиц является функцией координат и времени V = ƒ (t, x, y, z). Совокупность величин x, y, z, t называется переменными Эйлера.
Движение газа по методу Эйлера задается следующим образом:
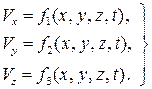(2.1)
Предполагая движение газа непрерывным, будем считать указанные функции однозначными, непрерывными и дифференцируемыми функциями координат x, y, z и времени t. В этом случае для нахождения траектории частиц газа следует в уравнениях (2.1) заменить 
на производные 
и интегрировать следующую систему дифференциальных уравнений:
(2.2)
После интегрирования системы (2.2) получим
где a, b, c – произвольные постоянные, значения которых определяются исходя из начальных условий. Исключим время t и получим уравнение траектории частицы газа.
Проекции ускорения газовых частиц в переменных Эйлера следующие:
где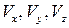 
– функции от x, y, z; x, y, z – функции от t.
По правилу дифференцирования сложной функции
. (2.3)
Так как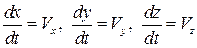 
, то выражения для проекций ускорения запишутся в виде
Следует помнить, что когда берутся полные производные, то учитывается не только изменение времени t, но и изменение координат (в зависимости от времени – x (t), y (t), z (t)) частицы газа при ее движении по траектории. Частные производные 
называются конвективными. Конвективная производная отражает то обстоятельство, что скорость движения изменяется при перемещении из одной точки пространства в другую. Конвективное ускорение имеет место практически всегда при стационарном и нестационарном движениях. Оно может быть равно нулю только тогда, когда 
.
Частные производные по времени берутся при фиксированных значениях координат и называются локальными (местными) производными. Локальная производная характеризует нестационарность процесса. При стационарном движении локальное ускорение 
всегда равно нулю. При нестационарном движении оно равно нулю только тогда, когда в данной точке скорость имеет экстремальное (максимальное или минимальное) значение во времени.
Метод Лагранжа. В методе Лагранжа фиксируются индивидуальные частицы газа и рассматривается их движение вдоль собственных траекторий. Так как газовых частиц бесчисленное множество, то охарактеризуем каждую частицу. В качестве характеристики частицы выберем ее координаты в начальный момент времени t = t 0 (a, b, c). Это означает, что из всей совокупности траекторий данной частице будет принадлежать та, которая проходит через точку a, b, c. Таким образом, координаты данной частицы x, y, z зависят от a, b, c, t – переменных Лагранжа, т. е.
. (2.4)
Уравнения (2.4) – это параметрические уравнения семейства траекторий, заполняющих все пространство, занятое газом.
Таким образом, если в методе Эйлера траектории движения частиц получаются интегрированием дифференциальных уравнений (2.2), то в методе Лагранжа они заданы функциями (2.4), из которых могут быть найдены проекции скорости и ускорения частиц:
, 
,
, 
,
, 
.
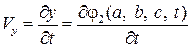Однако для решения большинства практических задач аэродинамики нет необходимости знать траектории движения частиц. Чаще всего нужно иметь данные о величине скорости в данной точке пространства вне зависимости от индивидуальности частицы, проходящей через нее. Этим практическим вопросам отвечает метод Эйлера, который как наиболее простой чаще всего применяется в аэродинамике.
Линии тока и траектории
Методу Лагранжа отвечает понятие траекторий частиц. Траектория представляет собой линию, изображающую путь, пройденный в пространстве частицей за некоторый отрезок времени.
Методу Эйлера соответствует понятие линий тока жидкости. Рассмотрим в момент времени t поле скоростей потока жидкости. Общую картину течения можно получить, если провести в потоке движущейся жидкости линии, совпадающие с направлением вектора скорости. Пусть вектор скорости в некоторой точке 1 пространства равен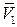 
(рис. 2.1). В этот же момент t в другой точке 2, расположенной на векторе 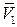и очень близкой к точке 1, вектор скорости равен 
, и т. д. В результате такого построения получаем ломаную линию 1 – 2 – 3 – 4 – 5 …, обладающую тем свойством, что вектор скорости, соответствующий начальной точки каждого звена, направлен вдоль этого звена. Устремив к нулю длину каждого отрезка, получаем кривую, называемую линией тока. Линиятока – мгновенная линия, вдоль которой в данный момент времени двигается совокупность частиц.
Если движение неустановившееся, то в следующий момент времени скорость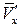 
в точке 1 отлична от предыдущего значения. Поэтому, проводя дальнейшие рассуждения и построения, аналогичные предыдущим, придем к иной кривой (к другой линии тока).
Линией тока называется линия, касательная к каждой точке которой совпадает по направлению с вектором скорости в данный момент времени.
Если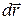 
– элемент линии тока, то из условия, что на линии тока ║ 
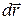, можно записать следующие уравнения:
(2.5)
которые являются дифференциальными уравнениями линий тока.
Семейство линий тока дает картину течения в данный момент времени, можно сказать, моментальный снимок направлений скоростей потока.
Через каждую точку пространства может проходить множество траекторий частиц, они могут пересекаться и пересекать сами себя.
Линии тока не пересекаются ни сами с собой, ни с другими линиями тока, так как вектор скорости в одной точке пространства не может иметь два разных значения в данный момент времени. Исключение составляют лишь особые точки, в которых скорость V = 0 (критические точки или точки торможения) или V = ∞ (исток, сток). Критическая точка – точка потока, в которой вектор скорости равен нулю, т. е. одновременно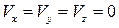 
. Для системы уравнений линий тока (2.5) эта точка является особой, в ней может нарушаться теорема единственности решения. Через критическую точку может проходить несколько и даже бесконечно много линий тока. Аналогичный вывод можно получить для источника и стока. Для этих кинематических образов значение скорости в их центрах обращается в бесконечность. Следовательно, и они являются особыми точками для системы уравнений (2.5).
Необходимо четко представлять разницу между линией тока и траекторией движения частицы. Если траектория отражает изменение положения частицы с течением времени, то линия тока указывает направление скоростей разных частиц в один и тот же момент времени. И только при установившемся движении линия тока совпадает с траекторией частицы. В этом случае траектории всех частиц, проходящих через какую-либо точку пространства, будут одинаковыми, следовательно, в каждый момент времени все частицы, которые лежат на траектории, будут образовывать и линию тока. В случае неустановившегося движения линии тока и траектория частицы не совпадают.
Уравнения траектории следующие: 
Поверхность тока – поверхность, построенная для фиксированного момента времени, в каждой точке которой вектор скорости лежит в касательной плоскости. Если выделить в движущейся жидкости некоторый бесконечно малый замкнутый контур, через каждую точку которого можно провести линию тока, то совокупность всех линий тока образует замкнутую поверхность – трубку тока (рис. 2.2). Жидкость, движущуюся внутри трубки тока, называют элементарной струйкой.
Трубка тока – простой и наглядный кинематический образ. Разбив весь поток на достаточно узкие трубки тока, можно, пользуясь основным свойством трубки – непроницаемостью ее боковой поверхности, изучать бесконечно малые перемещения выделенного объема жидкости. Между двумя произвольными линиями тока количество протекающей жидкости постоянно, поскольку вектор скорости лежит в касательной плоскости к поверхности трубки тока. То же самое можно сказать и о трубке тока: расход жидкости через любое сечение трубки тока одинаков.
Движение жидкой частицы
В кинематике твердого тела доказывается, что в общем случае движение твердого тела в каждый момент времени складывается из поступательного перемещения и вращения вокруг некоторой оси (мгновенной оси вращения). Движение жидкой частицы гораздо сложнее, так как она в процессе движения еще и деформируется.
Рассмотрим в момент времени t движение бесконечно малой частицы жидкости (рис. 2.3). Пусть точка М частицы имеет скорость, проекции которой равны 
, 
, 
в системе координат OXYZ. Поместим в эту точку начало системы координат Mx 1 y 1 z 1.
Тогда в некоторой точке 
на поверхности частицы с координатами 
проекции скорости равны
Применим к полученной системе разложение в ряд Тейлора и, сохраняя только величины первого порядка малости (члены с 
и 
в степени не выше первой), получим следующее:
,
, (2.6)
.
Преобразуем эти выражения: прибавим к правой части первого уравнения (2.6) величины 
и 
и перегруппируем члены:
Аналогично преобразуем второе и третье уравнения системы (2.6), дополнениями которых являются члены 
, 
и 
Введем следующие обозначения:
, 
, 
,
, 
,
, 
.
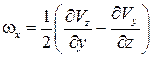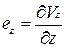Тогда преобразованные выражения (2.6) для проекций вектора скорости можно записать следующим образом:
(2.7)
Введем функцию 
. Ее производные по координатам 
равны
, 
,
.
Теперь перепишем систему уравнений (2.7) с помощью функции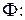 
(2.8)
Выясним физический смысл каждого из слагаемых, входящих в выражения (2.8):
1. 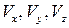– это проекции скорости поступательного движения рассматриваемой частицы в пространстве твердого тела.
2. 
, 
, 
– проекции угловой скорости вращения частицы жидкости (как твердого тела) вокруг мгновенной оси, проходящей через точку М. Такое вращательное движение называется вихревым движением, а компоненты угловой скорости 
– компонентами вихря. Угловая скорость вращательного движения равна 
, где 
– так называемый ротор или вихрь вектора скорости:
= 
– 
,
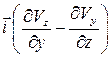где 
– операция градиента, т. е. 
.
Физически неравенство нулю значения 
в какой-либо точке потока означает, что в этой точке имеет место вращение элементарного объема. Составляющие угловой скорости вращения равны
. (2.9)
3. 
. Смысл этих слагаемых можно выяснить, исходя из простых физических соображений. Ясно, что жидкая частица при движении деформируется, и эти члены представляют собой не что иное, как скорости деформации частицы. Поясним это на примере.
Пусть бесконечно малая частица имеет в момент t форму прямоугольного параллелепипеда. Рассмотрим его проекцию на плоскость XY (рис. 2.4, прямоугольник МВDС). Компоненты скорости в точке М 
равны 
. Составляющие скорости в точках В 
и С 
с точностью до малых первого порядка можно представить в виде
, 
,
, 
,
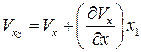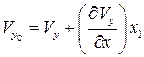или, так как рассматривается перемещение точек С и В относительно точки М, то
, 
,
, 
.
Очевидно, что 
и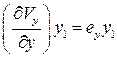 
есть скорости линейной деформации ребер прямоугольника. 
и 
указывают на поворот ребер МС и МВ, т. е. скорости деформации скашивания прямоугольника в некоторый косоугольник. Ребро МС поворачивается со скоростью 
, МВ – со скоростью 
, т. е. скорость изменения прямого угла ВМС складывается из угловых скоростей вращения ребер МС и МВ и, следовательно, представляет собой сумму 
. Аналогичные рассуждения можно провести для других проекций параллелепипеда.
Отсюда следует, что – компоненты скорости деформации жидкой частицы. Следовательно, формулы (2.8) подтверждают следующее:
Элементарное перемещение частицы жидкости (газа) состоит из поступательного перемещения ее центра со скоростью 
, вращения относительно некоторой оси, проходящей через этот центр с угловой скоростью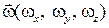 
, и деформационного движения, характеризуемого функцией 
.
Эта теорема (первая теорема Гельмгольца) является основной теоремой кинематики жидкой среды. То есть движение жидкой частицы в общем случае можно разложить на поступательное движение, вращательное движение и движение от деформации, которая состоит из линейной деформации и деформации скашивания. Такое разложение наиболее правильно с динамической точки зрения, так как оно разделяет движения, происходящие от сил разной природы.
