ТЯГА ДВИЖИТЕЛЯ
Теорема импульсов и ее применение для определения тяги. Тягой называется реактивная сила, которая развивается движителем в результате его взаимодействия с рабочим телом. Тяга возникает вследствие того, что движитель отбрасывает рабочее тело в сторону, противоположную полету, действуя на него с определенной силой. С такой же силой, но противоположно направленной, рабочее тело воздействует на движитель, образуя реактивную силу (тягу).
Тяга рассчитывается с помощью теоремы импульсов, согласно которой изменение полного импульса потока рабочего тела, проходящего через замкнутый контур, равно равнодействующей всех внешних сил, приложенных к объему рабочего тела, заключенного в этом контуре.
На рис. 6.1 показан замкнутый контур, который образован двумя сечениями, расположенными перпендикулярно потоку (сечением Н невозмущенного потока перед движителем и сечением С на выходе из движителя),
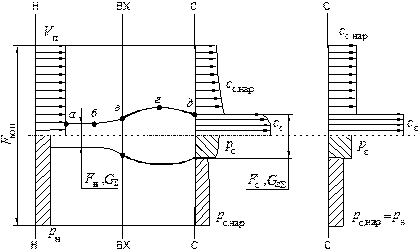
Рис. 6.1. Скорость потока и давление в характерных сечениях контура
и цилиндрической поверхностью, расположенной на достаточно большом расстоянии от движителя. Сечение Н и цилиндрическая поверхность выбираются на таком расстоянии от движителя, на каком параметры потока можно считать невозмущенными: давление равно атмосферному, а скорость потока равна скорости полета (движитель предполагается неподвижным, а воздух – движущимся со скоростью полета).
Для выбранного контура теорема импульсов может быть записана следующим образом:
P эф = Ф с – Ф н. (6.1)
Здесь Ф – полный импульс потока в данном сечении, равный сумме динамического и статического импульсов:
Ф = dG + dF. (6.2)
В уравнении (6.1) P эф – эффективная тяга (реактивная сила, которая направлена против направления движения потока). Она представляет собой равнодействующую всех сил, приложенных к внутренним и внешним поверхностям движителя.
Чтобы рассмотреть силы, возникающие на внутренней и наружной сторонах кругового контура абвгд, запишем уравнение (6.1) для потока, проходящего через движитель, и потока, обтекающего его:
P эф = (Ф с – Ф н) вн + (Ф с – Ф н) нар.
Обозначив изменение полного импульса для внутреннего и наружного потоков через Р' и X ', запишем
P эф = P' + X '. (6.1а)
Согласно теореме импульсов P' = (Ф с – Ф н) вн – результирующая всех сил, действующих на контур абвгд со стороны внутреннего потока; X ' = (Ф с – Ф н) нар – результирующая всех сил, действующих на тот же контур со стороны наружного потока. Подчеркнем, что в общем случае полный импульс – величина векторная, а результирующая сила должна определяться как разность векторов. В рассматриваемом случае поток не изменяет своего направления, а величины P' и X ' представляют собой проекции указанных сил на ось двигателя.
Теорема импульсов имеет универсальный характер и по ней, аналогично тому, как определяется сила P', можно рассчитать результирующий вектор сил, приложенных к внутренним поверхностям любого узла или элемента двигателя. Например, разностью полных импульсов в сечениях на выходе из сопла (Ф с) и на входе в него (Ф т), см. рис. 1.2, определяется проекция на ось сопла сил, приложенных к его внутренним поверхностям (включая силу атмосферного давления).
Вывод формул внутренней, эффективной и удельной тяги. Силы действия потока на контур складываются из сил нормального давления рабочего тела на этот контур и тангенциальных сил трения. Проекции этих сил на ось движителя определяются по уравнению импульсов, так как изменение полного импульса рассматривается только в направлении оси движителя (радиальные составляющие этих сил уравновешиваются, так как контур абвгд – круговая поверхность и поток осесимметричный).
Пользуясь формулой (6.2), выразим силы P' и X ' через параметры потока:
P' = с dG г S + с dF – G S V п – F н p н;
X ' = с нар dG нар + с нар dF нар – G нар V п – (F кон – F н) p н.
Заменяя истинные значения скорости и давления в сечении С их осредненными значениями (см. рис. 6.1) и предполагая, что среднее давление в сечении С для наружного потока равно атмосферному, получаем
P' = G г S c с + F с pс – G S V п – F н p н; (6.1б)
X ' = G нар (c с нар – V п) + F н p н – F с p н. (6.1в)
Сила P' – положительна, а X ' – отрицательна, т.е. направлена по движению потока. Причем величина p н (F н – F с) представляет собой проекцию на ось двигателя силы атмосферного давления, действующего на контур абвгд со стороны наружного потока.
Подставляя уравнения (6.1б) и (6.1в) в формулу (6.1а), получаем
P эф = G S (c с n c – V п) + F с (p с – p н) + G нар (c с нар – V п),
где n c = G г S / G S – коэффициент изменения массы рабочего тела между сечениями Н и С.
В полученном уравнении обозначим:
P = G S (c с n c – V п) + F с (p с – p н), (6.3)
X = G нар (c с нар – V п). (6.3а)
Тогда
P эф = P + X. (6.3б)
Силы P и X меньше рассмотренных ранее значений P' и X ' на величину p н (F н – F с).
Реактивную силу Р называют внутренней тягой или просто тягой движителя. Внутренняя тяга является результирующей сил нормального избыточного (по сравнению с атмосферным) давления и тангенциальных сил трения, действующих на контур абвгд со стороны рабочего тела, проходящего через движитель. Точнее, сил, действующих на все внутренние поверхности движителя и, кроме того, на жидкий контур абв. Согласно (6.3), внутренняя тяга зависит от параметров потока в сечениях С и Н. Если давление в сечении С равно атмосферному p с = p н, то
P = G S (c с n c – V п). (6.3в)
Отношение тяги к расходу воздуха через движитель называют удельной тягой движителя (или удельной тягой двигателя). При p с = p н
P уд = P / G S = c с n c – V п. (6.4)
Коэффициент n с, входящий в формулы (6.3) и (6.4), изменяется обычно в пределах 1,01 … 1,04. Поэтому при качественном анализе влияния различных факторов на параметры ГТД в целях упрощения формул он принимается равным единице (гл. 6, 7, 9 и др.), а при термогазодинамическом расчете двигателя его необходимо учитывать (гл. 8).
Удельная тяга движителя определяется приращением скорости рабочего тела в движителе относительно скорости полета. Абсолютная тяга, согласно (6.3в), пропорциональна, кроме того, расходу рабочего тела через движитель.
В формуле для эффективной тяги P эф (6.3б) сила X(как и X ')отрицательна (в уравнении (6.3а) скорость потока c с нар < V п) и выражает внешнее сопротивление движителя. Эффективная тяга, таким образом, равна разности между внутренней тягой и силой внешнего сопротивления движителя. Она затрачивается на совершение полезной работы по преодолению внешнего сопротивления летательного аппарата и его инерции. Внутренняя тяга затрачивается, кроме того, для преодоления внешнего сопротивления, создаваемого в полете самим движителем.
Образование и место приложения тяги.Следует помнить, что тяга является результирующей всех сил, приложенных ко всем поверхностям движителя. Известное утверждение: "Тяга образуется в сопле и приложена к соплу" – ошибочное в принципе. Тяга образуется во всех элементах, где есть изменение полного импульса, и приложена соответственно ко всем элементам движителя.
На примере дозвукового идеального ПВРД легко увидеть (рис. 6.2), что к соплу приложена составляющая тяги, направленная в сторону, противоположную полету P = P вх – P с. Составляющие тяги – проекции на ось двигателя сил избыточного (над атмосферным) давления на входное устройство P вх и сопло P с можно примерно оценить, имея в виду, что p с = p н и p г = p в. Тогда, принимая среднее избыточное давление на единицу поверхности входного устройства и сопла одинаковым и равным (p в– p н) / 2, будем иметь: P вх = (F mid – F н) (p в– p н) / 2 и P с = (F mid – F с) (p в– p н) / 2. Величина P вх > P с, так как F с > F н, что следует из условия неразрывности потока для сечений Н и С:
Рис. 6.2. Места приложения тяги
дозвукового идеального ПВРД
|
=.
Так как для идеального ПВРД p *с= p *н и l с= l п, то
F с / F н =.
Тяга передается от движителя к летательному аппарату через подвески двигателя, а также через все узлы, которые крепятся непосредственно к ЛА.
ТРД И ТВД КАК ЧАСТНЫЕ СЛУЧАИ ТРДД
В пятой главе отмечалось, что полезно используемое тепло цикла ГТД затрачивается в общем случае на приращение кинетической энергии рабочего тела, проходящего через основной контур двигателя, и на создание избыточной работы на валу турбины (5.6). Проследим за дальнейшим преобразованием избыточной работы турбины ГТД, являющегося двигательной установкой летательного аппарата (рис. 6.3).
В двухконтурном ТРД избыточная работа турбины передается компрессору наружного контура. Пренебрегая механическими потерями в трансмиссии на эту передачу, запишем уравнение баланса мощностей турбины N тII и компрессора N кII наружного контура:
N тII = N кII.
Представим величину мощности в виде произведения удельной работы на секундный расход рабочего тела; тогда, пренебрегая изменением массы рабочего тела в проточной части двигателя, получим
L тII G I = L кII G II,
| ||||
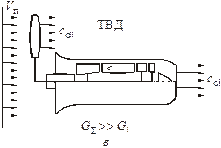
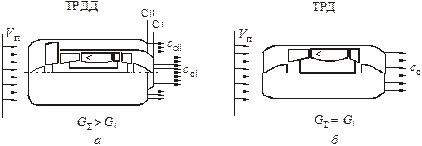
| Рис. 6.3. Схемы движителей: а – ТРДД; б – ТРД; в – ТВД |
или
L тII = L кII m, (6.5)
где m = G II/ G I – степень двухконтурности.
Работу L кII, подведенную к 1 кг воздуха, проходящего через наружный контур, выразим через кинетическую энергию на основании уравнения энергии, записанного для сечений Н и СII:
iн + + LкII = i сII +,
откуда
LкII =Lr II +,
гдеLr II = iсII – iн – потери тепла с рабочим телом, выходящим из наружного контура (рис. 6.4).
Эти потери возникают вследствие того, что часть механической энергии затрачивается на преодоление гидравлических сопротивлений в наружном контуре, преобразуясь в тепловую энергию, что приводит к увеличению температуры рабочего тела.
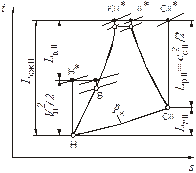Рис. 6.4. Диаграмма i-s рабочего
процесса в наружном контуре ТРДД
|
Подставляя полученное выражение для LкII в (6.5), а (6.5) – в (5.6), получим
L e =+
+ m + Lr II m. (6.6)
Уравнение (6.6) выведено для двухконтурного двигателя, но оно справедливо и для ТВД. В этом случае под т понимается отношение расхода воздуха через винт (G II) к расходу воздуха через двигатель, а под Lr II – потери в винте. Полученное уравнение справедливо и для ТРД, таккак для случая т= 0 его можно представить в виде равенства (5.6) при Lт II = 0.
Из уравнения (6.6) следует, что работа цикла любого из трех основных типов ГТД складывается из приращения кинетической энергии рабочего тела, проходящего через основной и наружный контуры двигателя (для ТРДД) или через основной контур и винт (для ТВД), и работы, затраченной на преодоление гидравлических потерь. Подчеркнем, что величина L e определяется в расчете на 1кг рабочего тела, проходящего через внутренний (основной контур).
Как показано в разд. 6.1, приращение скорости рабочего тела приводит к возникновению тяги. Следовательно, тяга создается и основным контуром двигателя, и наружным контуром ТРДД, и винтом ТВД. Все это – движители. Необходимо, однако, иметь в виду, что в ТРД и ТРДД скорость рабочего тела увеличивается в процессе расширения газа. Такие движители называются струйными; они отличаются от винтовых, в которых механическая энергия вращения преобразуется в приращение кинетической энергии путем отбрасывания винтом массы проходящего через него воздуха.
ТРД и ТВД являются, таким образом, частными случаями ТРДД. Степень двухконтурности рассматриваемых двигателей лежит в следующих пределах:
m = 0 – для ТРД;
m = 0,2... 10 – для современных ТРДД;
m = 15... 20 – для разрабатываемых ТРДДсв;
m = 25... 100 – для ТВ(В)Д с самолетным винтом (винтовентилятором);
m = 500... 1000 – для ТВаД с вертолетным (несущим) винтом.
Итак, три типа ГТД отличаются друг от друга прежде всего по степени двухконтурности, и, как будет показано далее, их основные особенности являются следствием этого различия.
