Варианты контрольных работ
Контрольная работа 1(1 семестр) 4
Контрольная работа 2 (2 семестр) 9
Контрольная работа 1(1 семестр)
Тема 1. Матрицы и определители
1.1. Вычислить определитель.
1. 
| 2. 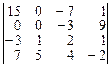
|
3. 
| 4. 
|
5. 
| 6. 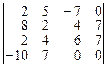
|
7. 
| 8. 
|
9. 
| 10. 
|
1.2. Найти обратную матрицу для матрицы А и сделать проверку.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 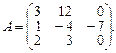
| 8. 
|
9. 
| 10. 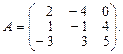
|
Тема 2. Системы линейных уравнений
Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса или методом Жордана–Гаусса.
1. 
| 2. 
|
3. 
| 4. 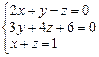
|
5. 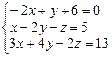
| 6. 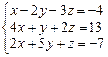
|
7. 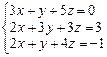
| 8. 
|
9. 
| 10. 
|
Тема 3–4. Векторная алгебра. Уравнение прямой
По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.
1. А(1; 2); В (–1; 2); С(3; 0).
2. А(3; 3); В(–3; –3); С(3; 5).
3. А(–1; 1); В(5; 1); С(3; 7).
4. А(3; 1); В (3; –5); С(–1; –1).
5. А(0; 5); В(5; 0); С(9; 3).
6. А(0; 0); В (8; 2); С(–2; 6).
7. А(–1; 4) В(–1; 2); С(–7; 3).
8. А(2; –1); В(5; 3); С(5; –2).
9. А(3; –3); В(7; –3); С(5; 5).
10. А(9; 0); В(5; 5); С(0; 3).
Тема 4. Уравнение плоскости
Даны точки М1 и М2.
Составить уравнение плоскости, проходящей через точку ш1 перпендикулярно вектору 
Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость.
1. М1 (–3; 2; 1); М2 (1; 2; 3).
2. М1 (2; –1; 3); М2 (1; 3; 1).
3. М1 (5; –4; 1); М2 (3; 2; 1).
4. М1 (–2; 3; 1); М2 (1; 1; 4).
5. М1 (–1; 4; 3); М2 (2; 5; 1).
6. М1 (2; –1; 5); М2 (–2; 1; 3).
7. М1 (3; 2; –2); М2 (5; 1; 2).
8. М1 (2; –5; 4); М2 (1; 3; 4).
9. М1 (2; 2; –1); М2 (1; 3; 1).
10. М1 (4; –2; 1); М2 (3; 1; 2).
Тема 5. Линии второго порядка
Составьте уравнение окружности с центром в заданной точке А и данным радиусом R. Сделать чертеж.
1. А(1; –7); R = 1.
2. А(–2; 6); R = 2.
3. А(–3; 2); R = 3.
Найти координаты вершин, оси, фокусы и эксцентриситет эллипса. Сделать чертеж.
4. 16x2 + 25y2 = 400.
5. 4x2 + 9y2 = 36.
6. 9x2 + 16y2 = 144.
По заданному уравнению гиперболы найти: координаты вершин, координаты фокусов, эксцентриситет, уравнение асимптот. Сделать чертеж.
7. 4x2 – 5y2 – 100 = 0.
8. 9x2 – 4y2 – 144 = 0.
Показать, что уравнение представляет собой уравнение параболы, найти: вершину, ось, директрису параболы.
9. 4x2 + 4x – 8y – 19 = 0.
10. 2x2 + 6x + y + 4 = 0.
Тема 6. Пределы функций
Вычислить пределы.
1. а)  б)
б)  в)
в) 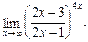
2. а) 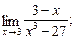 б)
б)  в)
в) 
3. а)  б)
б)  в)
в) 
4. а)  б)
б)  в)
в) 
5. а)  б)
б) 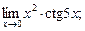 в)
в) 
6. а) 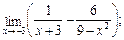 б)
б)  в)
в) 
7. а)  б)
б)  в)
в) 
8. а)  б)
б)  в)
в) 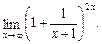
9. а) 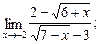 б)
б)  в)
в) 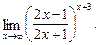
10. а)  б)
б)  в)
в) 
Тема 7. Основы дифференцирования
Найти производную сложной функции.
1. 
| 2. 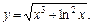
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 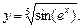
|
9. 
| 10. 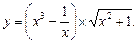
|
Тема 8. Исследование функций
Исследовать функцию и построить ее график.
1. 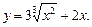
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 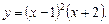
|
Контрольная работа 2 (2 семестр)
Тема 9. Неопределенный интеграл
Вычислить неопределенный интеграл.
1. а)  ; б)
; б) 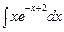 ; в)
; в)  ;
;
г)  .
.
2. а)  ; б)
; б) 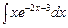 ; в)
; в) 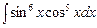 ; г)
; г) 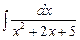 .
.
3. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
4. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 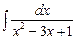 .
.
5. а)  ; б)
; б) 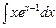 ; в)
; в)  ;
;
г)  .
.
6. а)  ; б)
; б)  ; в)
; в) 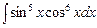 ; г)
; г)  .
.
7. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
8. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 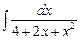 .
.
9. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
10. а) 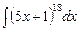 ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
Тема 10. Определенный интеграл
10.1. Вычислить определенный интеграл.
1. а)  ; б)
; б)  .
.
2. а)  ; б)
; б)  .
.
3. а) 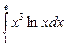 ; б)
; б)  .
.
4. а)  ; б)
; б)  .
.
5. а)  ; б)
; б)  .
.
6. а)  ; б)
; б) 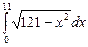 .
.
7. а) 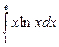 ; б)
; б)  .
.
8. а)  ; б)
; б)  .
.
9. а)  ; б)
; б)  .
.
10. а)  ; б)
; б)  .
.
10.2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж.
1. 
2. 
3. 
4. 
5. 
6. 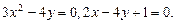
7. 
8. 
9. 
10. 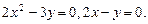
Тема 11. Несобственный интеграл
Вычислить интеграл или установить его расходимость.
1. а) 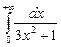 ; б)
; б)  .
.
2. а)  ; б)
; б)  .
.
3. а)  б)
б) 
4. а) 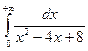 ; б)
; б)  .
.
5. а)  ; б)
; б)  .
.
6. а) 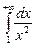 ; б)
; б) 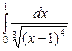 .
.
7. а)  ; б)
; б)  .
.
8. а)  ; б)
; б)  .
.
9. а) 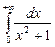 ; б)
; б) 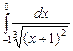 .
.
10. а)  ; б)
; б)  .
.
Тема 12. Ряды
12.1. Числовые ряды. Исследовать ряд на сходимость.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 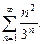
| 10. 
|
12.2. Степенные ряды. Определить область сходимости степенного ряда.
1. 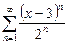 . .
| 2. 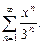
|
3. 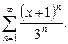
| 4.  . .
|
5.  . .
| 6. 
|
7. 
| 8. 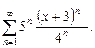
|
9. 
| 10. 
|
Тема 13. Функции нескольких переменных
Исследовать функцию на экстремум.
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 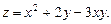
|
7. 
| 8. 
|
9. 
| 10. 
|
Тема 15. Решение дифференциальных уравнений
15.1. Найти общее и частное решения дифференциального уравнения.
1. 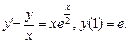
2. 
3. 
4. 
5. 
6. 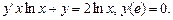
7. 
8. 
9. 
10. 
15.2. Найти общее решение дифференциального уравнения.
1. 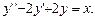
| 2. 
|
3. 
| 4. 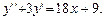
|
5. 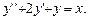
| 6. 
|
7. 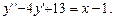
| 8. 
|
9. 
| 10. 
|
Тесты для промежуточного контроля знаний
1. Разложение по первой строке определителя  имеет вид:
имеет вид:
а) a11 + 2a12 – a13; б) 3a12; в) –a11 + 3a12; г) a11 + a12 + a13.
2. Даны матрицы 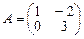 и
и  Тогда А – B равно:
Тогда А – B равно:
а)  б)
б)  в)
в)  г)
г) 
3. Матрица  не имеет обратной при λ, равном:
не имеет обратной при λ, равном:
а) –1; б) 0; в) –2; г) 1.
4. Система линейных уравнений с основной матрицей  и вектором правых частей
и вектором правых частей  имеет вид:
имеет вид:
а)  б)
б) 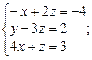
в)  г)
г) 
5. Длина отрезка, отсекаемого прямой 2x + 4y – 8 = 0 на оси Ox, равна:
а) 3; б) 5; в) 4; г) 8.
6. Найдите уравнение прямой, перпендикулярной прямой
y = –4x + 1:
а)  б)
б)  в)
в)  г)
г) 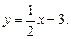
7. Координата x0 точки A(x0, 5, 10) принадлежащей плоскости 2x – y + z – 10 = 0, равна:
а) –2; б) 0; в) 2,5; г) 1.
8. Значение предела  равно:
равно:
а) 0; б) 5/3; в) 1; г) 3/5.
9. Закон движения материальной точки имеет вид x(t) = t3 – 4t, где x(t) – координата точки в момент времени t. Тогда скорость точки при t = 2 равна …
а) 24; б) 8; в) 18; г) 20.
10. На рисунке изображен график производной функции y = f(x), заданной на отрезке [–1; 8].

Тогда точкой максимума этой функции является:
а) 8; б) 0; в) 3; г) –1.
11. Множество первообразных функции f(x) = sin3x имеет вид:
а)  б)
б) 
в)  г)
г) 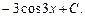
12. Вектор  перпендикулярен вектору
перпендикулярен вектору  , если λ равно:
, если λ равно:
а) 1; б) –2; в) –1; г) 2.
13. Векторы  и
и  коллинеарны, если k равно:
коллинеарны, если k равно:
а) 1; б) –2; в) –10; г) 4.
14. Если  и
и  , тогда скалярное произведение
, тогда скалярное произведение 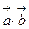 равно:
равно:
a) 5; б) 10; в) 7; г) 12.
15. Модуль комплексного числа 1 + i равен:
a)  б) 4; в) 7; г) 3.
б) 4; в) 7; г) 3.
16. Если z = 5 – 2i, то сопряженное ему комплексное число  равно:
равно:
a) 5 + 2i; б) –5 – 2i; в) 5i – 2; г) –5+2i.
17. Действительная часть комплексного числа (1 – i)2 равна:
a) 2; б) –1; в) 0; г) 1.
18. Значение функции f(z) = 3z – 1 в точке z0 = 1 + 2i равно:
a) –2 + 6i; б) 2 + 6i; в) –1 + 4i; г) –2 + 5i.
19. Периодической является функция:
a) f(x) = x + x2; б) f(x) = sin(x + π); в) f(x) = lnx; г) f(x) = 5π.
20. Для периодической функции f(x) с периодом T = 3, при всех x из области определения, выполняется равенство:
a) f(x + 3) = f(x); б) f(x – 3) = f(x);
в) f(3x) = f(x); г) f(x/3) = f(x).
21. Если 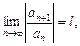 то числовой ряд сходится при l, равном:
то числовой ряд сходится при l, равном:
a) 0,5; б) 1; в) –2; г) 2.
22. Общий интеграл дифференциального уравнения  имеет вид:
имеет вид:
a)  б)
б) 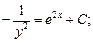
в)  г)
г) 
23. Дано дифференциальное уравнение 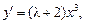 тогда функция y = x4 является его решением при λ, равном:
тогда функция y = x4 является его решением при λ, равном:
a) 2; б) 1; в) 3; г) 0.
24. Дано дифференциальное уравнение  Тогда соответствующее ему характеристическое уравнение имеет вид:
Тогда соответствующее ему характеристическое уравнение имеет вид:
a)  б)
б) 
в) 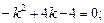 г)
г) 
25. Частная производная по y функции 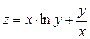 равна:
равна:
a)  б)
б) 
в)  г)
г) 






