Как обыкновенные дифференциальные уравнения, так и уравнения в частных производных можно разделить на линейные и нелинейные. Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Для таких уравнений решения образуют аффинное подпространство пространства функций. Теория линейных ДУ развита значительно глубже, чем теория нелинейных уравнений.
Линейным дифференциальным уравнением первого порядка называется уравнение вида
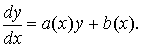
Здесь a (x) и b (x) — известные, непрерывные на [ a; b ] функции.
Доказано, что если функции a (x) и b (x) непрерывны на [ a; b ], то для любой начальной точки (x 0, y 0), x 0∈ [ a; b ], задача Коши
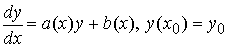
имеет единственное решение y = y (x) на [ a; b ].
Рассматривают однородные и неоднородные линейные уравнения первого порядка:
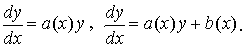
Общее решение линейного уравнения 1-го порядка можно найти с помощью замены y (x) = u (x) · v (x).
Общее решение линейного дифференциального уравнения первого порядка

с непрерывными на [a;b] коэффициентами a(x) и b(x), вычисленное методом вариации произвольной постоянной (методом Лагранжа), записывается в виде
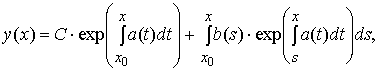
где C — произвольная постоянная, x0∈ [a; b], x∈ [a; b].
Найдём методом вариации произвольной постоянной (методом Лагранжа) общее решение линейного дифференциального уравнения 1-го порядка
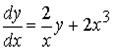
и решение задачи Коши
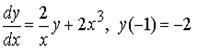
Сначала рассмотрим соответствующее однородное уравнение:

Это уравнение — уравнение с разделяющимися переменными, решение которого легко найти:
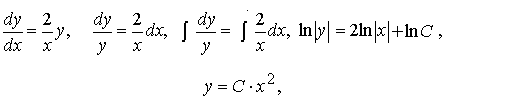
где C — произвольная постоянная.
Теперь будем искать решение неоднородного линейного уравнения в виде

где C (x) — неизвестная функция. В этом собственно и состоит метод Лагранжа — метод вариации (изменения) произвольной постоянной.
Подставляя выражение для y (x) в исходное неоднородное уравнение, получаем:
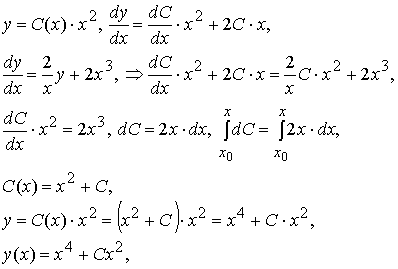
где C — произвольная постоянная. Теперь найдём решение задачи Коши:

Таким образом получено общее решение линейного дифференциального уравнения 1-го порядка
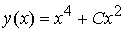
и решение задачи Коши

На рисунке изображены интегральные кривые уравнения (чёрный цвет) и график решения задачи Коши (красная линия).

Уравнения Бернулли.
Уравнением Бернулли называется уравнение первого порядка вида

Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции, n > 1.
Заменой z (x) = y 1- n (x) уравнение Бернулли сводится к линейному уравнению относительно функции z (x):

Получили линейное относительно z (x) уравнение:

Пример:
Уравнение Бернулли
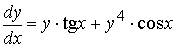
заменой z (x) = y −3(x) при y ≠ 0 сводится к линейному уравнению относительно функции z (x):
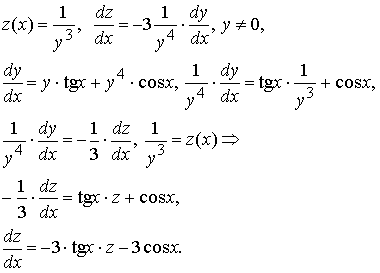
Линейное уравнение

решим методом Лагранжа (вариацией произвольной постоянной):

Выполнив обратную подстановку z (x) = y −3(x), получим при y ≠ 0 общий интеграл исходного уравнения:

Не следует забывать, что y = 0 — ещё одно решение уравнения.
Уравнение
M (x, y)d x + N (x, y)d y = 0
называется уравнением в полных дифференциалах, если выражение в левой части уравнения является дифференциалом некоторой функции двух переменных F (x, y), т.е. если
d F (x, y) = M (x, y)d x + N (x, y)d y.
Тогда F (x, y) = C — общий интеграл уравнения. Здесь C — произвольная постоянная.
Уравнение M (x, y)d x + N (x, y)d y = 0 являетсяется уравнением в полных дифференциалах, тогда и только тогда, когда 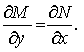
Пусть выражение M (x, y)d x + N (x, y)d y в левой части уравнения M (x, y)d x + N (x, y)d y = 0 является дифференциалом некоторой функции двух переменных F (x, y):
d F (x, y) = M (x, y)d x + N (x, y)d y.
Равенство d F (x, y) = M (x, y)d x + N (x, y)d y имеет место тогда и только тогда, когда функции M (x, y) и N (x, y) непрерывны вместе со своими частными производными первого порядка в некоторой односвязной области, 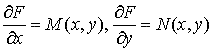 и
и 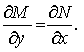
Отсюда следует, что уравнение M (x, y)d x + N (x, y)d y = 0 является уравнением в полных дифференциалах тогда и только тогда, когда 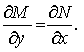
Список литературы
1. Методы, теории обыкновенных дифференциальных уравнений. Н.И. Гаврилов. Государственное издательство «Высшая школа» Москва-1962г.
2..В.В.Пак., Ю.Л. Носенко. Высшая математика: Учебник.- Д.: Сталкер,
1997г.
3. Степанов В.В. Курс дифференциальных уравнений (8-е изд.). М.: ГИФМЛ, 1959






