Общее решение неоднородного линейного ДУ является суммой общего решения 
соответствующего однородного ДУ и некоторого частного решения 
неоднородного ДУ, т.е. 
.
1) Решим сначала соответствующее однородное ДУ.
Характеристическое уравнение однородного ДУ 
имеет вид: 
.
Корни характеристического уравнения равны: 
Общее решение однородного ДУ запишется в виде
2) Частное решение неоднородного ДУ будем искать методом неопределённых коэффициентов.
Функция в правой части 
имеет специальный вид: 
Число 
не является корнем характеристического уравнения, а многочлен 
имеет нулевую степень, следовательно, частное решение неоднородного уравнения надо искать в виде: 
, где 
– неопределенный коэффициент.
Тогда 
, 
Подставим , 
и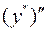 
в исходное уравнение, получим:
Общее решение неоднородного ДУ будет иметь вид:
.
Найдем частное решение. Имеем 
Для определения 
и 
используем начальные условия:
Итак: 
– частное решение неоднородного уравнения, соответствующее заданным начальным условиям.
Ответ: 
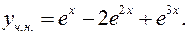
б) Операторный метод.
Найдем изображение по Лапласу для каждой функции.
Положим 
, где 
– оригинал,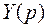 
– изображение,
(см. таблицу оригиналов и изображений).
По теореме о дифференцировании оригинала имеем:
;
.
Составим операторное уравнение:
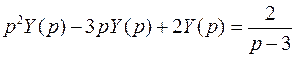, откуда выразим
.
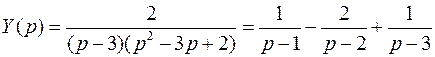Замечание. Разложение на простейшие дроби выполняется с помощью метода неопределенных коэффициентов.
Возвращаясь к оригиналу, по таблице найдем:
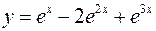– частное решение исходного ДУ.
Заметим, что решения, найденные в пунктах а) и б) совпадают.
Ответ: .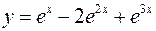
11. Найти общее решение ДУ: 
.
Решение.
Данное ДУ содержит в правой части две функции специального вида. Будем искать его решение в виде: 
, где 
– общее решение однородного уравнения, а 
и 
– некоторые частные решения неоднородного уравнения, соответствующие каждой из функций.
Характеристическое уравнение 
имеет корни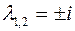 
.
Тогда общее решение соответствующего однородного уравнения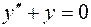 
имеет вид:
.
Будем интегрировать уравнение (11) отдельно для каждого слагаемого, стоящего в правой части уравнения.
1) 
;
Частное решение ищем в виде: 
.
Методом неопределенных коэффициентов находим: 
.
2) 
;
Частное решение ищем в виде: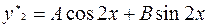 
.
Методом неопределенных коэффициентов находим: 
.
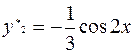Окончательно имеем: 
– общее решение неоднородного уравнения.
Ответ: 
.
12. Найти общее решение ДУ: 
.
Решение.
Данное уравнение является линейным однородным ДУ третьего порядка с постоянными коэффициентами.
Его характеристическое уравнение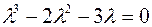 
имеет корни
Тогда общее решение имеет вид: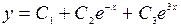 
.
Ответ: .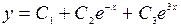
13. Найти частное решение системы: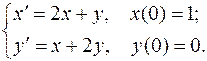 
Решение.
Решим эту систему тремя способами: а) методом сведения системы к одному ДУ; б) алгебраическим методом и в) операторным методом.
Заметим, что независимой переменной в данном примере является 
, а 
и 
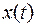– искомые функции.
