Решение примеров типового варианта
1. Найти общий интеграл дифференциального уравнения. Ответ представить в виде  (x,y)=C.
(x,y)=C.
а) 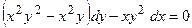 ,
,  ,
, 
Решение. Разделим переменные. Для этого преобразуем данное уравнение, вынося общий множитель слева  :
:  .
.
Разделим правую и левую части равенства на произведение множителей, стоящих не у своих дифференциалов, т.е. на  :
:
 , или
, или  , или
, или  .
.
Проинтегрируем обе части последнего равенства:  , или
, или 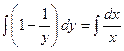 , или
, или  , откуда
, откуда  - общий интеграл данного уравнения.
- общий интеграл данного уравнения.
2. Найти решение задачи Коши
а)  , если
, если  при
при  .
.
Решение. Разделив все члены данного уравнения на  , приведем его к виду
, приведем его к виду
 Имеем линейное уравнение вида
Имеем линейное уравнение вида  . Здесь
. Здесь  ,
,  .
.
Решим уравнение методом Бернулли. Положим  , откуда
, откуда  .
.
Подставим эти значения в уравнение:  Сгруппируем члены, содержащие, например
Сгруппируем члены, содержащие, например  , и вынесем
, и вынесем  за скобку
за скобку  .
.
Выберем функцию  так, чтобы выражение в скобках обратилось в нуль. Тогда дифференциальное уравнение разобьется на два дифференциальных уравнения с разделяющимися переменными:
так, чтобы выражение в скобках обратилось в нуль. Тогда дифференциальное уравнение разобьется на два дифференциальных уравнения с разделяющимися переменными: 
Решаем уравнение (1) при  :
:  ,
,  .Интегрируя почленно, имеем:
.Интегрируя почленно, имеем:
 , или
, или  ,или
,или  . Подставим это значение в уравнение (2):
. Подставим это значение в уравнение (2): 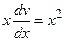 или
или  .
.
Интегрируя почленно, имеем:  или
или  .
.
Заменив в подстановке  функции
функции  и
и  их выражениями из равенств (1) и (2), получим искомое общее решение данного уравнения:
их выражениями из равенств (1) и (2), получим искомое общее решение данного уравнения:
 , или
, или  .
.
Найдем частное решение, удовлетворяющее начальным данным  при
при  . Для этого подставим в найденное общее решение начальные условия: Получим
. Для этого подставим в найденное общее решение начальные условия: Получим 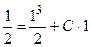 или
или  .
.
Искомое частное решение данного уравнения имеет вид  .
.
Замечание. Искомое решение уравнения  можно найти методом Лагранжа.
можно найти методом Лагранжа.
Соответствующее однородное уравнение есть  или
или  .
.
Разделяя переменные, получим  , откуда
, откуда  или
или 
Это решение однородного уравнения.
Считая С функцией от x, дифференцируя, находим

Подставляя y и  в исходное дифференциальное уравнение
в исходное дифференциальное уравнение 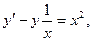 получаем
получаем  или
или 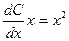 . Откуда
. Откуда  .
.
Отсюда получаем выражение С через x:

Итак, общее решение уравнения будет  или
или  .
.
b)  при
при  ,
,  .
.
Решение. Составим характеристическое уравнение  .
.
Найдем корни полученного квадратного уравнения:  , откуда
, откуда  и
и  . Так как корни действительные и
. Так как корни действительные и  , то общее решение имеет вид
, то общее решение имеет вид  . Подставляя найденные значения
. Подставляя найденные значения  и
и  в формулу общего решения, имеем:
в формулу общего решения, имеем:  .
.
Дифференцируя общее решение, получим
 .
.
Согласно заданным начальным условиям имеем
 , или
, или  ,
,
или  , или
, или  , откуда
, откуда
 и
и 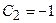 . Таким образом, искомым частным решением является функция
. Таким образом, искомым частным решением является функция  .
.
3. Найти общее решение дифференциального уравнения.
b) 
Решение. Общее решение исходного линейного неоднородного уравнения имеет вид  , где
, где  – общее решение соответствующего однородного дифференциального уравнения
– общее решение соответствующего однородного дифференциального уравнения  ,
,  – частное решение исходного неоднородного дифференциального уравнения.
– частное решение исходного неоднородного дифференциального уравнения.
Характеристическое уравнение  имеет корни
имеет корни  откуда общее решение однородного уравнения имеет вид:
откуда общее решение однородного уравнения имеет вид: 
Частное решение подбираем методом неопределенных коэффициентов. Правая часть дифференциального уравнения имеет специальный вид первого типа  , т.к.
, т.к. 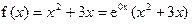 . Корень
. Корень  не является корнем характеристического уравнения, не имеет кратности. Поэтому частное решение неоднородного уравнения следует искать в виде
не является корнем характеристического уравнения, не имеет кратности. Поэтому частное решение неоднородного уравнения следует искать в виде 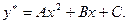 Для определения неизвестных коэффициентов А, В и С находим:
Для определения неизвестных коэффициентов А, В и С находим:
 ,
, 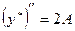 .
.
Подставляя  ,
,  и
и  в исходное дифференциальное уравнение, получаем равенство:
в исходное дифференциальное уравнение, получаем равенство:  или
или

Приравнивая коэффициенты при одинаковых степенях x, получаем систему

из которой находим 

Общее решение исходного дифференциального уравнения имеет вид:

 .
.
в). 
Решение. Общее решение исходного линейного неоднородного уравнения имеет вид  , где
, где  – общее решение соответствующего однородного дифференциального уравнения
– общее решение соответствующего однородного дифференциального уравнения  ,
,  – частное решение исходного неоднородного дифференциального уравнения.
– частное решение исходного неоднородного дифференциального уравнения.
Характеристическое уравнение  имеет корни
имеет корни  , откуда общее решение однородного уравнения имеет вид
, откуда общее решение однородного уравнения имеет вид 
Частное решение подбираем методом неопределенных коэффициентов.
Правая часть дифференциального уравнения имеет специальный вид второго типа  , так как
, так как  , где
, где  . Здесь
. Здесь  Комплексные числа
Комплексные числа  являются корнями характеристического уравнения
являются корнями характеристического уравнения  и имеют кратность. Поэтому частное решение неоднородного уравнения следует искать в виде
и имеют кратность. Поэтому частное решение неоднородного уравнения следует искать в виде
 или
или
Для определения неизвестных коэффициентов А1, В1, А2 и В2 подставляем  ,
,  и
и  в исходное дифференциальное уравнение, получаем равенство:
в исходное дифференциальное уравнение, получаем равенство:
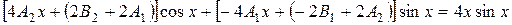
Приравнивая коэффициенты при одинаковых степенях x, получаем систему

Из системы находим  так что
так что 
Общее решение исходного уравнения есть






