Вариант 1
1. Найти интеграл, используя свойства линейности:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
2. Найти интеграл методом подстановки:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
3. Интегрирование по частям:
1)  2)
2)  3)
3) 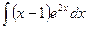
4. Найти интегралы:
1) 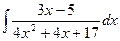 2)
2)  3)
3) 
5. Найти интегралы от рациональных дробей:
1) 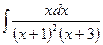 2)
2)  3)
3) 
6. Вычислить интегралы:
1)  2)
2)  3)
3) 
7. Вычислить площадь плоских фигуры, ограниченной линиями:

8. Вычислить двойные интегралы:






9. Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а) 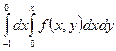 б)
б) 
10. Решить дифференциальные уравнения 2-го порядка:
1 
2 
3 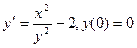
4 
5 
6 
7 
8 
9 
10 
11. Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные: б) неоднородные:
1  1
1 
2  2
2 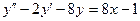
3  3
3 
Вариант 2
1. Найти интегралы, используя свойство линейности:
1).  2).
2). 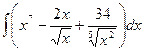
3).  4).
4). 
5).  6).
6). 
7).  8).
8). 
9).  10).
10). 
2. Найти интегралы методом подстановки:
1).  2).
2). 
3).  4).
4). 
5).  6).
6). 
7). 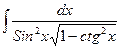 8).
8). 
9).  10).
10). 
11).  12).
12). 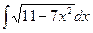
3. Интегрирование по частям:
1). 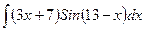 2).
2).  3).
3). 
4. Найти интегралы:
1).  2).
2).  3).
3). 
5. Найти интегралы от рациональных дробей:
1).  2).
2).  3).
3). 
6. Вычислить интегралы:
1).  2).
2).  3).
3). 
7. Вычислить площадь плоской фигуры, ограниченной линиями:
а). 
 и осью абсцисс
и осью абсцисс
б). 

8. Вычислить двойные интегралы:
а)  б)
б)  в)
в) 



9. Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а). 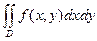 б).
б). 

10. Решить дифференциальные уравнения 1-го порядка:
1. 
2. 
3. 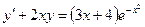
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а). однородные: б). неоднородные:
1.  1.
1. 
2.  2.
2. 
3.  3.
3. 
Вариант 4
1.Найти интегралы, используя свойство линейности:
1).  2).
2). 
3).  4)
4) 
5)  6)
6) 
7)  8)
8) 
9) 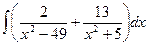
 10)
10) 
2.Найти интеграл методом подстановки:
1) 
 2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 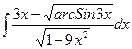
9)  10)
10) 
11)  12)
12) 

3.Интегрирование по частям:
1) 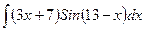 2)
2)  3)
3) 
4.Найти интегралы:
1)  2)
2)  3)
3) 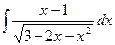
5.Найти интегралы от рациональных дробей:
1)  2)
2)  3)
3) 
6.Вычислить интегралы:
1)  2)
2) 
 3)
3) 
7.Вычислить площадь плоской фигуры, ограниченной линиями:
а) y = Inx, x = e и осью абсцисс
б) y = 2py, x 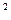 = 2py
= 2py
8.Вычислить двойные интегралы:
а)  б)
б)  в)
в) 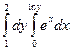


9.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)  б)
б) 

 x
x 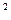 - 2x + y
- 2x + y 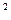 = 0 D – круг x
= 0 D – круг x 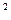 + y
+ y 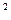
 2y
2y
x 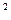 - 4x + y
- 4x + y 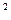 = 0
= 0
D: y = 
y = 0
10.Решить дифференциальные уравнения 1-го порядка:
1) y  = x(y
= x(y  +8) 2) y
+8) 2) y  =
=  , y(1) =
, y(1) = 
3) y  = 2xy + x
= 2xy + x  4) y
4) y  =
= 
5) sin 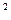 xdy = 3y
xdy = 3y 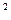 dx, y
dx, y  = 1 6) y
= 1 6) y  - y
- y 
7) xy  + y = y
+ y = y 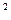 8) y
8) y  + ytgx = sin y
+ ytgx = sin y 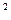 , y(0) = 1
, y(0) = 1
9) (5  )dx + xdy = 0 10) xdy = (y + x
)dx + xdy = 0 10) xdy = (y + x 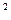 )dx
)dx
11. Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные: б) неоднородные:
1) y  + 2y
+ 2y  - 15y = 0 1) y
- 15y = 0 1) y  - y
- y  - 30y = - 6x - 1
- 30y = - 6x - 1
2) y  + 20y
+ 20y  + 100y = 0 2) y
+ 100y = 0 2) y  - 30y
- 30y  - 225y = 5e
- 225y = 5e  , y(2) = 0, y
, y(2) = 0, y  (2) = -1
(2) = -1
3) y  + 6y
+ 6y  + 25y = 0 3) y
+ 25y = 0 3) y  + 8y
+ 8y  + 52y = -sin5x + 2cos5x
+ 52y = -sin5x + 2cos5x
Вариант 5
1. Найти интегралы, используя свойство линейности:
1) 
3) 

5) 
7) 
9) 
2) 
4) 
6) 
8) 
10) 
2. Найти интегралы методом подстановки:
1) 
3) 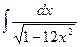
5) 

7) 
9) 
11) 
2) 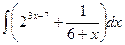
4) 
6) 
8) 
10) 
12) 
3. Интегрирование по частям:
1)  2)
2)  3)
3) 
4. Найти интегралы:
1)  2)
2)  3)
3) 
5. Найти интегралы от рациональных дробей:
1)  2)
2) 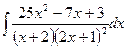 3)
3) 
6. Вычислить интегралы:
1)  2)
2)  3)
3) 
7. Вычислить площадь плоской фигуры, ограниченной линиями:
а)  ,
, 
б)  ,
, 
8. Вычислить двойные интегралы:
а
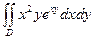

б


в


9. Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)


б)

D- круг удовлетворяющий неравенству 
10. Решить дифференциальные уравнения 1-го порядка:
1) 
2)  ,
, 
3) 
4)  ,
, 
5) 
6) 
7) 
8)  ,
, 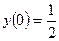
9) 
10) 
Решить линейные дифференциальные уравнения с постоянными коэффициентами
А) однородные б) неоднородные
1 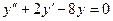
| 1 
|
2 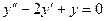
| 2 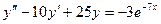 , ,  , , 
|
3 
| 3 
|
Вариант 11
1. Найти интегралы, используя свойство линейности:
1)  2)
2) 
3)  4)
4) 
5) 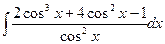 6)
6) 
7)  8)
8) 
9)  10)
10) 
2.Найти интегралы методом подстановки:
1)  2)
2) 
3) 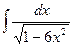 4)
4) 
5)  6)
6) 
7)  8)
8) 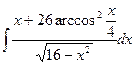
9) 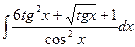 10)
10) 
11) 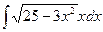 12)
12) 
3. Интегрировании е по частям:
1)  2)
2)  3)
3) 
4. Найти интегралы:
1)  2)
2)  3)
3) 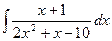
5. Найти интегралы от рациональных дробей:
1)  2)
2)  3)
3) 
6. Вычислить интегралы:
1) 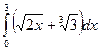 2)
2)  3)
3) 
7. Вычислить площадь плоской фигуры, ограниченной линиями:
а ) у=lnx, x=e и осью абсцисс
б) у2=2рх, х2=2ру
8. Вычислить двойные интегралы:






9. Перейти к полярным координатам и в пун6кте б) вычислить двойной интеграл:
а) 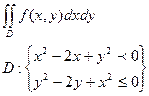 б)
б) 
10. Решить дифференциальные уравнения 1-го порядка:
1) y’=(4Sinx-x2)y
2) 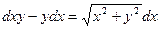
3) 
4) xy’+y3=1
5) 
6) dx=y(3x-4)dx
7) 
8) 
9) 
10) y’-2xy=3xy2
11. Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные: б) неоднородные:
1. y”+4y’-12y=0 1. y’+11y’+24y=-2x+3
2. y”+14y’+64y=0 2. y”+3y’-28y=2e3x,y(2)=0,y’(2)=-1
3. y”-6y’+18y=0 3. y”+28y’+196y=4Sin2x-3Cos2x
Вариант 14
1.Найти интегралы, используя свойство линейности:
1)  2)
2) 
3)  4)
4) 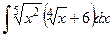
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
2.Найти интеграл методом подстановки:
1)  2)
2) 
3)  4)
4) 
5) 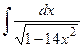 6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 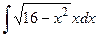
3.Интегрирование по частям:
1)  2)
2) 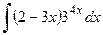 3)
3) 
4.Найти интегралы:
1)  2)
2)  3)
3) 
5.Найти интегралы от рациональных дробей:
1)  2)
2)  3)
3) 
6.Вычислить интегралы:
1)  2)
2)  3)
3) 
7.Вычислить площадь плоской фигуры, ограниченной линиями:
а)  и осью абсцисс
и осью абсцисс
б) 
8.Вычислить двойные интегралы:
а)  б)
б)  в)
в) 
D:  D:
D:  D:
D: 
9.перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а) б)


D:  D:
D: 
10.Решить дифференциальные уравнения 1-го порядка:
1 
2 
3 
4 
5 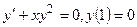
6 
7 
8 

9 
10 
11.Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные б) неоднородные
1.  1.
1. 
2.  2.
2. 
3. 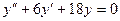 3.
3. 
Вариант15
1.Найти интегралы, используя свойство линейности:
1)  2)
2) 

3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
2. Найти интеграл методом подстановки:
1)  2)
2) 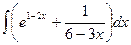
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
3. Интегрирование по частям:
1)  2)
2)  3)
3) 
4. Найти интегралы:
1)  2)
2)  3)
3) 
5.Найти интегралы от рациональных дробей:
1)  2)
2)  3)
3) 
6.Вычислить интегралы:
1)  2)
2)  3)
3) 
7.Вычислить площадь плоской фигуры, ограниченной линиями:
a)  и осью абсцисс
и осью абсцисс
б) 
8.Вычислить двойные интегралы:
a)  b)
b)  c)
c) 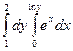


9.Перейти к полярным координатами в пункте б) вычислить двойной интеграл:
а)  б)
б) 
 D-круг
D-круг 
10.Решить дифференциальные уравнения 1-ого порядка:
1. 
2. 
3. 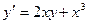
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11.Решить линейные дифференциальные уравнения с постоянным коэффициентами:
а) однородные б) неоднородные
1. 

 1.
1. 
2.  2.
2. 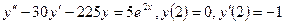
3.  3.
3. 
Вариант 17
1. Найти интегралы, используя свойство линейности:
1) 
 2)
2) 

3)  4)
4) 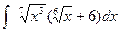
5)  6)
6) 
7)  8)
8) 
9) 
 10)
10) 
2. Найти интегралы методом подстановки:
1)  2)
2) 
3)  4)
4) 
5) 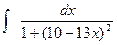 6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
3. Интегрирование по частям:
1)  2)
2) 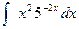 3)
3) 
4. Найти интегралы:
1) 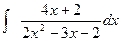 2)
2)  3)
3) 
5. Найти интегралы от рациональных дробей:
1)  2)
2)  3)
3) 
6. Вычислить интегралы:
1)  2)
2)  3)
3) 
7. Вычислить площадь плоской фигуры, ограниченной линиями:
а) y= - 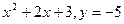
б) y= Sin x, y= Cos x, x=0
8. Вычислить двойные интегралы:
а)  б)
б) 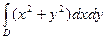 в)
в) 
D:  D:
D:  D:
D: 
9. Перейти к полярным координатам и в пункте б) вычислить интеграл:
а)  б)
б) 
D:  D:
D: 
10. Решить дифференциальные уравнения 1-го порядка:
1) 
2) 
3) 
4) 
5) 
6) 
7) xdy+ylnxdx=ylnydx, y(1)=1
8) SinyCosxdy=CosySinxdx
9) 
10) 
11. Решить линейные дифференциальные уравнения с постоянными коэффициентами:
а) однородные: б) неоднородные:
 1
1 
 2
2 
 3
3 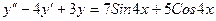
Вариант 18
1.Найти интегралы, используя свойство линейности:
1) 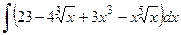 2)
2) 
3)  4)
4) 
5)  6)
6) 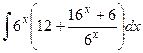
7) 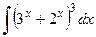 8)
8) 
9)  10)
10) 
2.Найти интегралы методом подстановки:
1)  2)
2) 
3)  4)
4) 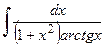
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
3.Интегрирование по частям:
1)  2)
2)  3)
3) 
4.Найти интегралы:
1)  2)
2)  3)
3) 
5.Найти интегралы от рациональных дробей:
1)  2)
2)  3)
3) 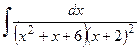
6.Вычислить интегралы:
1) 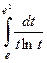 2)
2)  3)
3) 
7.Вычислить площадь плоской фигуры, ограниченной линиями:
а) 
б) 
8.Вычислить двойные интегралы:
а б в



D:  D:
D:  D:
D: 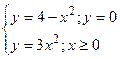
9.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а) б)


D:  D:
D: 
10.Решить дифференциальные уравнения 1-го порядка:
1 
2 <






