Нормальные алгоритмы были предложены в 1951 г. советским ученым А.А. Марковым. Как и машины Тьюринга, нормальные алгоритмы оперируют со словами в некотором алфавите. Главное же их отличие от МТ состоит в том, что нормальный алгоритм представляет собой не устройство, а некоторый упорядоченный набор элементарных операций над словами. Операндами этих операций в общем случае являются последовательности букв, что зачастую упрощает построение нормального алгоритма по сравнению с МТ.
Для изучения данной темы необходимо повторить понятия и определения символьных конструкций и операций над ними.
В литературе алгоритмы Маркова коротко описаны в работах [1,2,5].
Задание на самостоятельную работу
Контрольные вопросы:
- как функционирует нормальный алгоритм?
- чем отличается нормальный алгоритм в алфавите А от алгоритма над А?
- является ли любой нормальный алгоритм в А в то же время и алгоритмом над А? Справедливо ли обратное?
- в каких случаях нормальный алгоритм останавливается?
- приведите пример нормального алгоритма, работающего бесконечно;
- почему нельзя доказать принцип нормализации?
1. Составьте следующие нормальные алгоритмы Маркова над алфавитом А.
а) замена в слове a в алфавите 
каждого символа a на символ с;
б) нормальный алгоритм над любым алфавитом, который ничего не делает;
в) перестановка в слове a в алфавите 
букв таким образом, чтобы сначала стояли все нули, а потом все единицы;
г) сложение двух чисел X и Y в унарном коде. Исходное слово имеет вид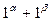 
;
д) вычисление функции 
в унарном коде. Исходное слово имеет вид: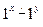 
;
е) вычисление функции 
в унарном коде.
ж) вычисление функции 
в унарном коде. Исходное слово имеет вид 
;
з) последователь 
в десятичной системе счисления;
и) алгоритм над алфавитом 
, исключающий в слове последнюю звездочку;
к) алгоритм над алфавитом 
, меняющий местами первую и последнюю буквы слова;
л) алгоритм над алфавитом 
, переставляющий буквы слова в обратном порядке;
м) алгоритм над алфавитом , меняющий местами первый 0 и последнюю единицу в слове;
н) алгоритм над алфавитом , выдающий в качестве результата 0, если исходное слово представляет собой четное двоичное число, и 1, если число нечетное;
о) алгоритм над алфавитом 
, который выдает 1, если исходное слово содержит комбинацию baccd, и 0 - в противном случае.
п) алгоритм над алфавитом ,который выдает 1, если в исходном слове содержатся только парные нули, и 0 - в противном случае;
р) алгоритм над алфавитом 
, который выдает «да», если в исходном слове четное количество y -ков, и «нет» в противном случае;
с) алгоритм над алфавитом , выдающий в результате столько единиц, сколько нулей в исходном слове;
т) алгоритм над алфавитом 
, выделяющий часть слова, расположенную между первой парой звездочек.
2. На конкретных примерах исходных слов продемонстрируйте работу составленных алгоритмов.
ЛИТЕРАТУРА
1. Алферова З.В. Теория алгоритмов. -М.:Статистика,1973.-164с.
2. Криницкий Н.А. Алгоритмы вокруг нас. -М: Наука, 1977.-126с.
3. Криницкий Н.А. Миронов Г.А., Фролов Г.Д. Программирование и алгоритмические языки. -М.Наука, 1979.-496с.
4. Кузнецов О.П. Адельсон-Вельский Г.М. Дискретная математика для инженера. -М.: Энергия, 1980.-344с.
5. Мальцев А.И. Алгоритмы и рекурсивные функции. -М.Наука, 1965.-392с.
6. Петер Р. Рекурсивные функции. -М.ИЛ, 1954.-366с.
7. Трахтенброт Б.А. Алгоритмы и вычислительные автоматы. -М.: Советское радио, 1974.-200с.
8. Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств. -М.:Наука, 1980.-400с.
9. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике.-М.:Наука, 1977.-368с.
10. Лавров И.А., Максимов Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. - М.: Наука, 1975.-240с.
