Задания
К практическим занятиям по курсу
“ДИСКРЕТНЫЕ СТРУКТУРЫ”
Донецк, 2012
Тема 1. ИНТУИТИВНОЕ ПОНЯТИЕ АЛГОРИТМА
Материал этой темы является вводным при изучении классической теории алгоритмов. Основные задачи изучения темы – повторение и закрепление понятия и свойств алгоритма, рассматриваемых в курсе «Программирование и работа на ЭВМ», дальнейшее развитие навыков алгоритмизации, демонстрация проявления основных свойств алгоритмов на конкретных примерах. Рекомендуемая литература: [1,2,3,4].
Задания на самостоятельную работу
Контрольные вопросы:
- в чем смысл интуитивного понятия алгоритма?
- назовите основные свойства алгоритмов. Как они проявляются в программах?
- в чем особенность рекурсивных алгоритмов?
Задачи.
1.Составьте следующие алгоритмы:
а) вычисление произведения двух целых чисел без использования операции умножения;
б) вычисление частного и остатка от деления двух целых чисел без использования операции деления;
в) перевод целого десятичного числа в P -ичную систему счисления;
г) подсчет количества делителей целого числа X;
д) вычисление n!, где n - любое целое число;
2. Выполните трассировку алгоритмов: Евклида, решета Эратосфена, разложения числа на простые множители по исходным данным в соответствии с вариантом задания.
| Алгоритм № п/п | Алгоритм Евклида | Решето Эратосфена | Разложение чисел на простые множители | |
| 2 3 | ||||
| 25 | 60 | 150 | 68 | |
| 70 | 42 | 160 | 36 | |
| 100 | 30 | 130 | 100 | |
| 85 | 60 | 200 | 96 | |
| 78 | 29 | 65 | 72 | |
| 36 | 48 | 112 | 106 | |
| 112 | 40 | 120 | 85 | |
| 30 | 120 | 250 | 48 | |
| 52 | 13 | 220 | 90 | |
| 72 | 38 | 80 | 200 | |
| 86 | 92 | 146 | 66 | |
| 40 | 100 | 150 | 70 | |
| 35 | 150 | 210 | 82 | |
| 128 | 192 | 160 | 30 | |
| 81 | 27 | 230 | 102 | |
| 68 | 96 | 125 | 78 | |
| 68 | 26 | 170 | 128 | |
| 64 | 160 | 240 | 86 | |
| 172 | 43 | 111 | 56 | |
| 105 | 50 | 195 | 44 | |
| 116 | 48 | 190 | 122 | |
| 256 | 64 | 99 | 108 | |
| 49 | 70 | 300 | 39 | |
| 26 | 104 | 119 | 115 | |
| 121 | 22 | 270 | 45 |
3. Отсортировать массив X с помощью методов вставок, слияния и «взбалтывания». Привести всю последовательность шагов алгоритма для заданного массива.
1. 7,1,4,9,53,39,33.
2. 87,72,41,12,50,67,52.
3. 15,23,85,19,56,13,55.
4. 15,70,81,57,36,16,85,46.
5. 11,73,14,24,28,29,43,27.
6. 35,47,33,11,18,38,94,36.
7. 80,25,95,20,62,53,56,62.
8. 24,99,23,83,12,75,12,2,14.
9. 17,68,18,16,19,71,87,11,59.
10. 12,14,51,13,71,89,39,16.
11. 11,66,12,79,22,87,21,19,20.
12. 26,27,95,30,11,62,29,45.
13. 80,72,73,81,38,46,24,30.
14. 32,14,79,27,79,58,69,74.
15. 67,37,73,83,29,81,16,53,94.
16. 25,65,19,99,26,74,32,33.
17. 106,274,301,221,241,188.
18. 13,52,11,73,25,91,26,82.
19. 46,95,43,50,76,45,57,61.
20. 10,31,34,11,7,17,18,58,24.
21. 24,28,61,19,27,15,95,26.
22. 20,86,16,19,81,71,26,82.
23. 96,86,73,42,46,27,39.
24. 14,79,37,11,34,36,38,46.
25. 18,16,26,23,24,29,31,32.
4. Составьте рекурсивные алгоритмы для вычисления:
а) суммы n элементов массива чисел;
б) произведения n элементов массива;
в) поиск максимального и минимального элементов в массиве чисел;
г) сортировка методом «взбалтывания». Указание: составить два рекурсивных алгоритма: один выполняет просмотр массива, другой – использует просмотры для сортировки всего массива;
д) поиск заданного элемента в неупорядоченном массиве;
е) поиск заданного элемента в упорядоченном массиве методом деления массива пополам.
5. Выполните трассировку рекурсивных алгоритмов:
а) игра «Ханойская башня» для n=3 и n=4;
б) функция «91»; в качестве n возьмите номер своего варианта, увеличенный на 30;
в) алгоритмы, указанные в п.4.
Тема 2. РЕКУРСИВНЫЕ ФУНКЦИИ
Рекурсивные функции представляют собой исторически первую формальную модель алгоритма. Они задают алгоритм как правило вычисления значения некоторой числовой функции. Ключевыми в данной теме являются понятия рекурсии и оператор примитивной рекурсии.
Рекурсия в самом общем виде – это есть правило определения (или построения) некоторого объекта с использованием его же самого.
Дадим некоторые важные определения.
Числовые функции, значения которых можно вычислять посредством единого для данной функции алгоритма, называются вычислимыми функциями. Вычислимая функция – интуитивное понятие, поскольку при ее определении использован термин «алгоритм».
Арифметическими называются функции, области определения и значений которых – натуральный ряд.
Арифметические функции с ограниченной областью определения называются частными, остальные – всюду определенными.
Для первоначального ознакомления с рекурсивными функциями рекомендуется литература [ 1,4,8 ]. Для более полного изучения можно воспользоваться монографией А.И. Мальцева [ 5 ] или Р. Петер [ 6 ]. Книга [ 6 ] вместе с тем написана достаточно просто и понятно даже для неподготовленного читателя.
Задания на самостоятельную работу
Контрольные вопросы:
- что такое частичные функции, вычислимые функции?
- перечислите простейшие функции, принятые в теории рекурсивных функций;
- что такое примитивно-рекурсивная функция?
- как доказать примитивную рекурсивность функции?
- являются ли примитивно-рекурсивные функции частичными или всюду определенными? Почему?
- что такое оператор минимизации? Когда он работает бесконечно?
- что такое общерекурсивная функция?
Задания
Показать, что функция f(n) - примитивно-рекурсивная. Привести тестовые примеры.
1. Сумма всех делителей n.
2. Количество взаимно простых с n чисел.
3. Количество нулей в двоичной записи n.
4. Сумма цифр в двоичной записи n.
5. Кол-во делителей числа n.
6. Максимальная цифра в 8-ричной записи n.
7. Минимальная цифра 8-ричной записи n.
8. Количество четных цифр в 8-ричной записи n.
9. Количество нечетных цифр в 8-ричной записи n.
10. Сумма простых делителей n.
11. Количество простых чисел, меньших либо равных n.
12. Количество чисел, меньших либо равных n, являющихся полными квадратами.
13. Сумма чисел, меньших либо равных n, являющихся степенью 2.
14. Максимальная цифра в 16-ричной записи n.
15. Минимальная цифра в 16-ричной записи n.
16. Ближайшее к n простое число.
17. Произведение простых делителей n.
18. Произведение взаимно простых с n чисел, меньших либо равных n.
19. Произведение нечетных делителей числа n, меньших либо равных n.
20. Произведение четных цифр 8-ричной записи числа.
21. MAX (НОД (n,m), HOK (n,m)).
22. Целая часть квадратного корня из n, 
.
23. Целая часть корня степени y из x, 
.
24. Целая часть exp(x), 
.
25. 
(=1 при y>=x)
26. Функция, перечисляющая по порядку числа Фибоначчи:
Задачи.
1.Доказать примитивную рекурсивность следующих функций и предикатов:
а) 
б) 
в) 
г) 
д) 
е) «ступенька»:
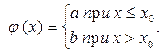
ж) функция, отличная от нуля в конечном числе точек;
з) s(х) - сумма делителей числа x, где s(0)=0
и) p(x) - произведение делителей числа х;
к) t (x) - количество делителей числа x;
л) предикат: Х - четное число
м) предикат: Х делится на n;
н) 
- число простых чисел, не превосходящих x:
о) K(x,y) - наименьшее общее кратное x и y, если K(x,0)=0 и K(0,y)=0;
п) d(x,y) - наибольший общий делитель чисел x и y, если d(0,0)=0;
р) 
- х-тое простое число 
с) 
, где 
т) 
2. Используя операторы суперпозиции и примитивной рекурсии, докажите примитивную рекурсивность следующих функций:
а) 
б) 
в) 
г) 
(сумма по модулю 2);
д) 
е) импликация x®y;
3. Пусть функции 
примитивно–рекурсивны. Доказать, что тогда примитивно–рекурсивны и следующие функции:
а) 
б) 
в) 
г) 
д) 
если верхний предел суммирования меньше нижнего, то сумма равна нулю.
е) 
если верхний предел меньше нижнего, произведение равно 1.
4. Пусть 
примитивно–рекурсивные функции. Докажите, примитивно–рекурсивна и 
, определяемая следующей схемой:
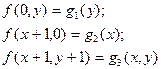
5. Приведите процесс вычисления функций по схеме примитивной рекурсии:
а) 
б)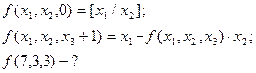 
в) 
г)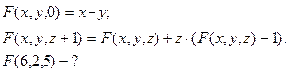 
д) 
е) 
ж) 
6. Докажите частичную рекурсивность следующих функций:
а) 
б)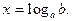 
7. Применив операцию минимизации к подходящей примитивно–рекурсивной функции, докажите, что функция 
является частично–рекурсивной:
а)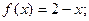 
б) 
в) 
г) 
д) 
8. Приведите процесс вычисления функций с использованием оператора минимизации:
а) 
б) 
в) 
г) 
Тема 3. МАШИНЫ ТЬЮРИНГА
Рекурсивные функции представляют алгоритм через вычислимую функцию, т.е. понятие «вычислимая функция» является первичным по отношению к понятию «алгоритм». Машины Тьюринга (МТ) являются в этом смысле более естественными, т.к. вначале уточняют понятие «алгоритм», а через него – вычислимую функцию.
Машина Тьюринга (Тьюринга-Поста, т.к. предложена ими почти одновременно и независимо в 1936-1937 гг.) построена на основе использования свойства детерминированности алгоритмов. Основной смысл этого свойства сводится к тому, что алгоритмический процесс должен выполнятся механически, т.е. может быть реализован машиной. Машина Тьюринга является абстрактной, т.к. имеет неограниченные ресурсы, что требуется для реализации любых алгоритмов.
В данной теме вводятся некоторые понятия символьных конструкций и операций над ними, описаны функционирование и способы задания МТ, способы композиции МТ, позволяющие строить сложные МТ из более простых, приводится понятие об эквивалентности МТ и рекурсивных функций.
Наиболее полно (в рамках программы курса) машины Тьюринга описаны в [ 1,4,8 ], приводится большое количество примеров. В [2] изложение более популярное и менее формализованное. Дополнительный материал о МТ можно найти в [7].
