ЗАНЯТИЕ 3. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.

Ауд.

Л-3

гл.10: № 67, 68, 74, 78, 83, 86, 92, 95,179, 193.

☺ ☻ ☺

Пример 1 – 67: Решить дифференциальное уравнение: y′ +2 xy = x . (1)

Решение:

1). Приводим уравнение к «стандартной форме»: y′ + P (x)∙ y = Q (x).

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде: функции y = u ∙ v.

a ¹. Вычислим интеграл: – и запишем: u = .

a ². Вычислим функцию v: v = +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = ∙ .

3). В нашем случае: уравнение линейное, имеет «стандартную форму»: y′ + P (x)∙ y = Q (x)!

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =–2 =– x ² → u = .

a ². Вычислим функцию v: v = +С= +С = = +С;

a ³. Запишем общее решение уравнения: y = u ∙ v = ∙ .

Ответ: y = u ∙ v = ∙ – общее решение.

Пример 2 – 68: Решить дифференциальное уравнение: y′ =3 + x.

Решение:

1). Приводим уравнение к «стандартной форме»: y′ –3 ∙ y = x.

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =3 =3ln| x | → u = = x ³.

Замечание: в последней записи выражения для u знак модуля опущен, так как от функции u (x) требуется только обеспечить выполнение равенства: u′ + P (x)∙ u =0 (см. вывод формулы для решения y = u (x)∙ v (x)!).

a ². Вычислим функцию v: v = +С= +С =– +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = x ³∙ = Сx ³– x ².

Ответ: y = u ∙ v = Сx ³– x ²– общее решение.

Пример 3 – 74: Решить дифференциальное уравнение: y′ = .

Решение:

1). Приводим уравнение к «стандартной форме»: x′ – ∙ x = y ². Переход от записи решения в виде y = y (x) к записи x = x (y) подсказан исходным выражением вполне выразительно!

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: x = u (y)∙ v (y).

a ¹. Вычислим интеграл: – = =ln| y | → u = = y.

Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68).

a ². Вычислим функцию v: v = +С= +С = y ²+С.

a ³. Запишем общее решение уравнения: x = u ∙ v = y ∙ = Сy + y ³.

Ответ: x = u ∙ v = Сy + y ³ – общее решение. Из исходного уравнения также: y =0 – решение.

Пример 4 – 78: Решить дифференциальное уравнение: xy′ + x ²+ xy = y.

Решение:

1). Приводим уравнение к «стандартной форме»: y′ + ∙ y = – x. Переход от записи решения в виде y = y (x) к записи x = x (y) подсказан исходным выражением вполне выразительно!

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u (x)∙ v (x).

a ¹. Вычислим интеграл: – = =ln| x |– x → u = = xe ^{– x} .

Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68).

a ². Вычислим функцию v: v = +С= +С =– e^x +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = xe ^{– x} ∙ = x ∙(С e ^{– x} –1).

Ответ: y = u ∙ v = x ∙(С e ^{– x} –1) – общее решение.

Пример 5 – 83: Решить дифференциальное уравнение: y′ + y∙tgx = , y (0)=0.

Решение:

1). Уравнение записано в «стандартной форме».

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =– =ln|cos x | → u = = cos x.

Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68).

a ². Вычислим функцию v: v = +С= +С = tgx +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = cos x ∙ = sin x + С cos x.

a ⁴. Найдем частное решение уравнения: 0= sin0+ С cos0 → С =0; y = sin x – частное решение уравнения для начальных условий: y (0)=0.

Ответ: y = sin x + С cos x – общее решение; y = sin x – частное решение.

Пример 6 – 86: Решить дифференциальное уравнение: y′ +4 xy =2 x ∙ ∙ . (1)

Решение:

1). Имеем уравнение (1) Бернулли в «стандартной форме».

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Примем: z = y ^–n+1;

a ¹. Запишем преобразованное уравнение Бернулли: z′ +(– n +1) P (x)∙ z =(– n +1) Q (x), или (для удобства!): z′ + P ₁(x)∙ z = Q ₁ (x);

a ². Решение уравнения ищем в виде функции: z = u (x)∙ v (x).

a ³. Вычислим интеграл: – → u = .

a ⁴. Вычислим функцию v: v = +С.

a ⁵. Запишем общее решение уравнения: z = u ∙ v = ∙ .

3). В нашем случае: уравнение Бернулли в «стандартной форме», для n = .

a ⁰. Примем: z = y ^–n+1, где (– n +1)= ; то есть: z = .

a ¹. Запишем преобразованное уравнение Бернулли: z′ + 4 x ∙ z = 2 x ∙ , или:

z′ +2 x ∙ z = x ∙ . (2)

a ². Решение уравнения ищем в виде функции: z = u (x)∙ v (x).

a ³. Вычислим интеграл: – =– =– x ² → u = = .

a ⁴. Вычислим функцию v: v = +С= x ²+С.

a ⁵. Запишем общее решение уравнения для (2): z = u ∙ v = ∙ . (3)

a ⁶. Учитывая: z = , запишем общее решение для (1): = ∙ .

Ответ: = ∙ – общее решение.

Пример 7 – 92: Решить дифференциальное уравнение: xy′ + y =2 x ²∙ ylny ∙ y′. (1)

Решение:

1). Очевидно: (1) не является уравнением Бернулли для y, y′. Это подсказывает необходимость перехода к функции x = x (y): x′ + x =2 lny ∙ x ². (2)

2). Получили уравнение (2) Бернулли в «стандартной форме», для n =2.

a ⁰. Примем: z = x ^–n+1, где (– n +1)= –1; то есть: z = x ^–1.

a ¹. Запишем преобразованное уравнение Бернулли: z′ – z = –2 lny. (3)

a ². Решение уравнения ищем в виде функции: z = u (y)∙ v (y);

a ³. Вычислим интеграл: – = =ln y → u = = y.

Замечание: в последней записи выражения для u знак модуля опущен, так как исходное выражение предполагает y >0.

a ⁴. Вычислим функцию v: v = = –2 +С= – ln ² y +С;

a ⁵. Запишем общее решение уравнения для (3): z = u ∙ v = y ∙ . (4)

a ⁶. Учитывая: z = x ^–1, запишем общее решение для (1): xy =1.

Ответ: xy =1 – общее решение уравнения.

Пример 8 – 95: Решить дифференциальное уравнение: ydx+ dy =0, y =1. (1)

Решение:

1). Очевидно: (1) не является уравнением Бернулли для y, y′. Это подсказывает необходимость перехода к функции x = x (y): x′ + x = x ³. (2)

3). Получили уравнение (2) Бернулли в «стандартной форме», для n =3.

a ⁰. Примем: z = x ^–n+1, где (– n +1)= –2; то есть: z = x ^–2.

a ¹. Запишем преобразованное уравнение Бернулли: z′ –2 z = –1. (3)

a ². Решение уравнения ищем в виде функци: z = u (y)∙ v (y);

a ³. Вычислим интеграл: – =2 =2ln| y | → u = = y ².

Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68). В то же время есть возможность записать: 2ln| y | = ln y ².

a ⁴. Вычислим функцию v: v = = – +С= +С.

a ⁵. Запишем общее решение уравнения для (3): z = u ∙ v = y ²∙ . (4)

a ⁶. Учитывая: z = x ^–2, запишем общее решение для (1): x ²(y + С y ²)=1.

a ⁷. Найдем частное решение для (1): так как (1 + С1²)=1 → С=3, то частное решение имеет вид: x ²(y +3 y ²)=1.

Ответ: x ²(y + С y ²)=1 – общее решение уравнения; частное решение: x ²(y +3 y ²)=1.

Пример 9 – 179: Найти уравнение кривой, проходящей через точку (1,0), если площадь трапеции, образованной касательной в этой точке, осями координат и ординатой точки касания, постоянна и равна .

Решение:

В Примере 1 – 19 получено выражение: отрезка А = OА =(0, y – y ′ х), – отсекаемого касательной на оси ординат.

1). Так как площадь трапеции вычисляется по формуле: S = h, где a и b – стороны оснований, h – высота трапеции, условие задачи запишем так:

▪ (ОА + ND)∙ ОD =2 S =3 → (y – y ′ х+y)∙ х = 3; (1)

▪ (ОА + ND)∙ ОD =2 S =3 → (y – y ′ х+y)∙ х =– 3. (2)

Случай-1.

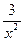2). Запишем (1), в виде: y ′– y =– – «стандартная форма» линейного уравнения.

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =2 =2ln| x | → u = x ².

a ². Вычислим функцию v: v = +С=–3 +С = x ^–3+С;

a ³. Запишем общее решение уравнения: y = u ∙ v = x ²∙(x ^–3+С)= +C x ².

a ⁴. Запишем частное решение уравнения: y = – x ², при С=–1.

Случай-2.

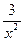3). Запишем (2), в виде: y ′– y = – «стандартная форма» линейного уравнения.

a ⁰. Решение уравнения ищем в виде: функцию y = u ∙ v.

a ¹. Вычислим интеграл: – =2 =2ln| x | → u = x ².

a ². Вычислим функцию v: v = +С= 3 +С =– x ^–3+С;

a ³. Запишем общее решение уравнения: y = u ∙ v = x ²∙(– x ^–3+С)=C x ²– . Это решение «симметрично относительно оси ОХ» решению, полученному в Случае-1.

a ⁴. Запишем частное решение уравнения: y = x ²– , при С=1.

4). Построим эскиз графика функции y = – x ², используя известные графики для гиперболы и параболы и применяя понятие «сумма функций» (см. рисунок).

Ответ: для Случая-1: y = – x ² – частное решение ДУ; для Случая-2: y = x ²– – частное решение ДУ.

Замечание: Если не заметить присутствия двух различных вариантов решения рассмотренной задачи, то «зеркальное решение» будет потеряно. В задачах физики это дополнительно подсказывает важность понимания начальных условий исследуемого процесса: возможно исследователю потребуются дополнительные эксперименты для уточнения особенностей протекания процесса.

Пример 10 – 193: Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1.5 м/с, скорость её через 4 секунды равна 1м/с. Когда скорость уменьшится до 1 см/с? Какой путь пройдет лодка до остановки?

Решение:

Для решения задачи необходимо уточнить: система координат, используемая при решении задачи, связана с берегом реки и считается инерциальной. Это значит, что второй закон Ньютона в этой системе выполняется и можно записать дифференциальное уравнение:

m∙v′ =– k∙v, (1)

где m – масса лодки с гребцом; k – коэффициент торможения лодки из-за сопротивления воды. Движение лодки происходит по инерции (гребец «сушит весла»!).

Обозначим: – =μ и запишем уравнение в виде, удобном для интегрирования:

= μ∙ dt. (2)

Интегрируя (2), получаем: v = v ₀ ∙e ^{μ t}, где v ₀=1.5 м/с. В задаче не определены ни движущаяся масса, ни коэффициент трения лодки о воду. Но мы имеем дополнительные сведения (легко устанавливается экспериментально!), которые позволят полностью определить закон движения лодки.

Из условия: для t =4c имеем v = 1 [м/с] → 1=1.5 ∙ e ^{μ 4} . Отсюда: (e ^μ) ⁴ = ≈ 0.67 и e ^μ ≈ =λ.

Итак, закон движения: v = v ₀ ∙λ^t. У нас v =1.5 ∙λ^t. После этого можем определить время, когда скорость лодки уменьшилась до 1 см/с: 0.01=1.5 ∙λ^t, откуда → t ≈ 50с.

Для ответа на второй вопрос необходимо проинтегрировать уравнение: dx =1.5 ∙λ^tdt. Примем, что начальное положение лодки: x ₀=0. Тогда x =1.5 ∙ =1.5 ∙lnλ (0– λ^t) ≈ 15м.

Замечание: при вычислении несобственного интеграла учтено, что для верхнего предела значение этого интеграла равно нулю!

Ответ: Время: t ≈ 50с. До полной остановки лодка переместится на расстояние x ≈ 15м (это будет проистекать бесконечно долго!).

* * * * * * * * * *

Домашнее задание

Дома

Л-2

гл.10: № 70, 71, 72, 75, 85, 87, 89, 94, 180, 198.

Пример 1 – 70: Решить дифференциальное уравнение: (1+ x ²) y′ = 2 xy +(1+ x ²)². (1)

Решение:

1). Так как заданное уравнение не «стандартной формы», приводим его к стандартной форме: y′ + P (x)∙ y = Q (x), то есть: y′ – 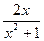y = x ²+1. (2)

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – и запишем: u = .

a ². Вычислим функцию v: v = +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = ∙ .

3). В нашем случае: уравнение линейное, имеет «стандартную форму»: y′ + P (x)∙ y = Q (x)!

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =– =–ln(x ²+1) → u = = x ²+1.

a ². Вычислим функцию v: v = +С= +С = x +С.

a ³. Запишем общее решение уравнения: y = u ∙ v =(x ²+1)∙(x +С).

Ответ: y = u ∙ v =(x ²+1)∙(x +С) – общее решение.

Пример 2 – 71: Решить дифференциальное уравнение: y′ +2 y = e ^{3 x} .

Решение:

1). Уравнение записано в «стандартной форме».

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =– =–2 x → u = = e ^{–2 x} .

a ². Вычислим функцию v: v = +С= +С = e ^{5 x} +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = e ^{–2 x} ∙ = e ^{3 x} +С e ^{–2 x} .

Ответ: y = e ^{3 x} +С e ^{–2 x} – общее решение.

Пример 3 – 72: Решить дифференциальное уравнение: y′ + =2 lnx +1.

Решение:

1). Приведём уравнение к «стандартной форме»: y′ + y =2 lnx +1.

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =– =– lnx → u = = .

a ². Вычислим функцию v: v = +С= +С =2 + +С. Если учесть «табличный» интеграл (легко получить интегрированием по частям!): = = lnx – , то: v = x ² lnx + – +С = x ² lnx +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = ∙ = xlnx + .

Ответ: y = xlnx + – общее решение.

Пример 4 – 75: Решить дифференциальное уравнение: (1+ x ²) dx =(arctgy – x) dy.

Решение:

1). Видим, что по y и y′ уравнение не приводится к линейному уравнению. Приведём уравнение к «стандартной форме» линейного по по x и x′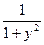: x′ + x = .

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: y = u ∙ v.

a ¹. Вычислим интеграл: – =– =– arctgy → u = = .

a ². Вычислим функцию v: v = +С= +С=[Примем: arctgy=t ]= = +С=[см. таблицу интегралов!]= te^t – e^t +С= arctgy – +С.

a ³. Запишем общее решение уравнения: y = u ∙ v = ∙ = = arctgy –1+C

Ответ: y = arctgy –1+C – общее решение.

Пример 5 – 85: Решить дифференциальное уравнение: y′ = , y (1)=1.

Решение:

1). Видим, что по y и y′ уравнение не приводится к линейному уравнению. Приведём уравнение к «стандартной форме» линейного по по x и x′: x′ + x =2 lny +1.

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде функции: x = u ∙ v.

a ¹. Вычислим интеграл: – =– =– lny → u = = .

a ². Вычислим функцию v: v = +С= +С =2 + +С. Если учесть результат Примера 3 – 72, то: v = y ² lny +С.

a ³. Запишем общее решение уравнения: x = u ∙ v = ∙(y ² lny +С) = ylny + .

a ⁴. Запишем частное решение уравнения: x = ylny + , так как С=1.

Ответ: x = ylny + – общее решение; частное решение: x = ylny + .

Пример 6 – 87: Решить дифференциальное уравнение: dy =(y²e^x – y) dx. (1)

Решение:

1). Из исходного уравнения: y =0–решение. Перепишем (1): y′ + y = e ^x∙ y ². (2)

2). Получили уравнение (2) Бернулли в «стандартной форме», для n =2.

a ⁰. Примем: z = y ^–n+1, где (– n +1)= –1; то есть: z = y ^–1.

a ¹. Запишем преобразованное уравнение Бернулли: z′ – z = – e ^x. (3)

a ². Решение уравнения ищем в виде функции: z = u (x)∙ v (x);

a ³. Вычислим интеграл: – = = x → u = = e ^x.

a ⁴. Вычислим функцию v: v = = +С= – x +С;

a ⁵. Запишем общее решение уравнения для (3): z = u ∙ v = e ^x ∙(С– x). (4)

a ⁶. Учитывая: z = y ^–1, запишем общее решение для (1): y ^–1= e ^x ∙(С– x).

Ответ: ye ^x ∙(С– x)=1 – общее решение уравнения, также y =0.

Пример 7 – 89: Решить дифференциальное уравнение: y′ = yctgx + . (1)

Решение:

1). Из исходного уравнения: y =0–решение. Перепишем (1): y′ – ctgxy = ∙ y ³. (2)

2). Получили уравнение (2) Бернулли в «стандартной форме», для n =3.

a ⁰. Примем: z = y ^–n+1, где (– n +1)= –2; то есть: z = y ^–2.

a ¹. Запишем преобразованное уравнение Бернулли: z′ + ctgx∙z = –2 . (3)

a ². Решение уравнения ищем в виде функции: z = u (x)∙ v (x);

a ³. Вычислим интеграл: – =–2 =–2 ln | sinx | → u = = .

a ⁴. Вычислим функцию v: v = = 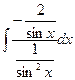+С=–2 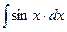+С=2 cosx +C;

a ⁵. Запишем общее решение уравнения для (3): z = u ∙ v = (2 cosx +C). (4)

a ⁶. Учитывая: z = y ^–2, запишем общее решение для (1): y ^–2= (2 cosx +C).

Ответ: sin ² x = y ²(2 cosx +C) – общее решение уравнения, также y =0.

Пример 8 – 94: Решить дифференциальное уравнение: 3 dy = –(1+3 y ³) y∙sinxdx, y =1. (1)

Решение:

1). Из исходного уравнения: y =0–решение. Перепишем (1): y′ + sinx∙y =– sinx∙y ⁴. (2)

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Примем: z = y ^–n+1, где (– n +1)= –3; то есть: z = y ^–3.

a ¹. Запишем преобразованное уравнение Бернулли: z′ – sinx∙z = 3 sinx. (3)

a ². Решение уравнения ищем в виде функции: z = u (x)∙ v (x);

a ³. Вычислим интеграл: – = =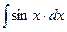– cosx → u = = e ^{– cosx}.

a ⁴. Вычислим функцию v: v = = + С = –3 + С =

=–3 e^cosx +С;

a ⁵. Запишем общее решение уравнения для (3): z = u ∙ v = e ^{– cosx} (–3 e^cosx +С). (4)

a ⁶. Учитывая: z = y ^–3, запишем общее решение для (1): y ^–3=C e ^{– cosx} –3.

a ⁴. Запишем частное решение уравнения: y ^–3=4 e ^{– cosx} –3, так как С=4.

Ответ: y ^–3=C e ^{– cosx} –3 – общее решение; частное решение: y ^–3=4 e ^{– cosx} –3.

Пример 9 – 180: Найти уравнение кривой, проходящей через точку (0,1), если площадь треугольника, образуемого осью абсцисс, касательной и радиус-вектором точки касания, постоянна и равна 1.

Решение:

В Примере 1 – 19 получено выражение: отрезка Т = OТ = , – отсекаемого касательной на оси абсцисс.

1). Так как площадь треугольника вычисляется по формуле: S = ah, где a –основание, h – высота треугольника, условие задачи запишем так:

▪ ОТ ∙ ND =2 S =2 → ∙ y =2; (1)

▪ ОT ∙ ND =2 S =–2 → ∙ y =–2 (2)

Случай-1.

2). Запишем (1), в виде: x ′– x =– – «стандартная форма» линейного уравнения.

a ⁰. Решение уравнения ищем в виде функции: x = u ∙ v.

a ¹. Вычислим интеграл: – = =ln| y | → u = y.

a ². Вычислим функцию v: v = +С=–2 +С = y ^–2+С.

a ³. Запишем общее решение уравнения: x = u ∙ v = y ∙(y ^–2+С)= +C y.

a ⁴. Запишем частное решение уравнения: x = – y, при С=–1.

Случай-2.

3). Запишем (2), в виде: x ′– x = – «стандартная форма» линейного уравнения.

a ⁰. Решение уравнения ищем в виде функции: x = u ∙ v.

a ¹. Вычислим интеграл: – = =ln| y | → u = y.

a ². Вычислим функцию v: v = +С=2 +С =– y ^–2+С;

a ³. Запишем общее решение уравнения: x = u ∙ v = y ∙(С– y ^–2)=C y – . Это решение «симметрично относительно оси ОХ» решению, полученному в Случае-1.

a ⁴. Запишем частное решение уравнения: x = y – , при С=1.

4). Построим эскиз графика функции x = – y, используя известные графики для гиперболы и прямой и применяя понятие «сумма функций» (см. рисунок: выделено красным).

Ответ: для Случая-1: x = – y – частное решение ДУ; для Случая-2: x = y – – частное решение ДУ.

Замечание: Если не заметить присутствия двух различных вариантов решения рассмотренной задачи, то «зеркальное решение» будет потеряно. В задачах физики это дополнительно подсказывает важность понимания начальных условий исследуемого процесса: возможно исследователю потребуются дополнительные эксперименты для уточнения особенностей протекания процесса.

Пример 10 – 198: Сила тока i в цепи с сопротивлением R, индуктивностью L и напряжением u удовлетворяет уравнению: L∙ + R∙i = u. Найти силу тока i в момент времени t, если u = Esinωt и i = 0 при t = 0 (L, R, E, ω – постоянные).

Решение:

1). Приведём уравнение к «стандартной форме»:

i′ + a ∙ i = b ∙ u: (1)

где a = и b = (принято для удобства записи).

2). Данное уравнение решаем, применяя общий алгоритм:

a ⁰. Решение уравнения ищем в виде: функцию i = z ∙ v.

a ¹. Вычислим интеграл: – =– a =– at → z = 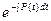= e ^{– at}.

a ². Вычислим функцию v: v = +С= b +С= bE +С. Вычислим интеграл: J= = [дважды применяется «интегрирование по частям», затем решение алгебраического равенства относительно символа J] = e^at ∙(a ∙ sinωt – ω ∙ cosωt). Тогда окончательно: v = bE ∙J+С, или v = bE ∙J+ bE ∙С= bE ∙(J+С). Последнее определяется «удобством!»: допустимо, так как bE – постоянная величина!

a ³. Запишем общее решение уравнения: i = u ∙ v = bE ∙ e ^{– at} ∙(J+С). (2)

a ⁴. Запишем частное решение уравнения из условия: i (0)=0 → легко вычисляется С= → частное решение: i = bE ∙ (a ∙ sinωt – ω ∙ cosωt + ω ∙ e ^{– at}). С учетом значений a и b получим окончательно: i = (R ∙ sinωt – Lω ∙ cosωt + Lω ∙ ).

Ответ: i = (R ∙ sinωt – Lω ∙ cosωt + Lω ∙ ) – частное решение.

☻

Вопросы для самопроверки:

1. Как определяют линейное дифференциальное уравнение 1-го порядка?

2. Что значит: «стандартная форма» линейного уравнения, зачем её вводят?

3. Какова основная «идея» способа «подстановки» решения линейного уравнения?

4. Всегда ли можно «проинтегрировать» линейное ДУ?

5. Какие уравнения относят к уравнениям Бернулли?

6. В чем особенность интегрирования уравнения Бернулли?

7. Бывают ли уравнения Бернулли, которые невозможно «проинтегрировать»?

< * * * * * >