Пусть дано диф. уравнение (4), разрешенное относительно производной
 (6)
(6)
, и пусть (5) есть общее решение данного уравнения. Это общее решение определяет семейство интегральных кривых на плоскости OXY.
Уравнение (6) для каждой точки M с координатами х и у определяет значение производной  , т.е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Диф. Ур. (6) определяет поле направлений на плоскости Оху.
, т.е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Диф. Ур. (6) определяет поле направлений на плоскости Оху.
Следовательно, с геометрической точки зрения задача интегрирования диф.ур. заключается в нахождении кривых, направление касательных которых совпадает с направлением поля в соотвествующих точках.
Для диф ур (2) геометрическое место точек, в которых выполняется соотношение  , называется изоклиной.
, называется изоклиной.
При различных значениях k получаем различные изоклины. Построив семейство изоклин можно приближенно построить семейство интегральных кривых.
Задача Коши для дифференциального уравнения первого порядка имеет вид:
 ;
;
 - начальное условие.
- начальное условие.
Теорема (Теорема существования и единственности решения задачи Коши). Если в уравнении (1.3) функция  и ее частная производная
и ее частная производная 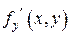 непрерывны в некоторой области
непрерывны в некоторой области  , содержащей точку
, содержащей точку 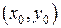 , то существует единственное решение
, то существует единственное решение  этого уравнения, удовлетворяющее начальному условию
этого уравнения, удовлетворяющее начальному условию  .
.
Уравнения 1-го порядка и методы их решений:
1.Уравнения с разделяющими переменными. Это уравнения вида (4), у которых  , или вида (3), у которых
, или вида (3), у которых  и
и  , где
, где  .
.
Решение. Уравнение (3) сводится к виду 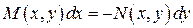 . Получим
. Получим  . Делим обе части на
. Делим обе части на  и интегрируем:
и интегрируем:  или
или  – общий интеграл данного уравнения.
– общий интеграл данного уравнения.
Деление на  может привести к потере частных решений, являющихся корнями уравнения
может привести к потере частных решений, являющихся корнями уравнения  . Наличие особых решений устанавливаем проверкой.
. Наличие особых решений устанавливаем проверкой.
Пример 1. Решить уравнение  при начальных условиях
при начальных условиях  .
.
Это уравнение является уравнением с разделяющимися переменными. Перенеся  в правую часть уравнения и учитывая, что
в правую часть уравнения и учитывая, что  , запишем:
, запишем:
 или
или  .
.
Разделив обе части последнего уравнения на  , получим уравнение
, получим уравнение  , которое уже является уравнением с разделенными переменными.
, которое уже является уравнением с разделенными переменными.
Проинтегрируем обе части уравнения  .
.
Интеграл 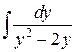 можно представить в виде
можно представить в виде
 .
.
Получим  .
.
Последнее выражение, записанное в виде  , называется общим интегралом соответствующего дифференциального уравнения.
, называется общим интегралом соответствующего дифференциального уравнения.
Для нахождения частного решения подставим в общий интеграл значения  ,
,  , то есть
, то есть  ,
,  :
:  , откуда следует, что
, откуда следует, что  .
.
Значит,  или
или  .
.
Ответ:  .
.


2. Однородные дифференциальные уравнения. Это уравнения вида  , в которых правую часть можно привести к виду
, в которых правую часть можно привести к виду  . Тогда
. Тогда
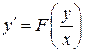 . (1.7)
. (1.7)
Для решения полагаем  , где
, где  . Имеем
. Имеем  ;
;  . Подставив это выражение в (1.7), получим
. Подставив это выражение в (1.7), получим  или
или  , т.е. уравнение с разделяющимися переменными. После решения заменим
, т.е. уравнение с разделяющимися переменными. После решения заменим  .
.
Пример 3. Решить уравнение  .
.
Это уравнение является однородным дифференциальным уравнением, т.к. в преобразованном виде  правая часть является однородной функцией нулевого порядка.
правая часть является однородной функцией нулевого порядка.
Уравнение 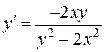 решаем заменой
решаем заменой  , где
, где  . Тогда
. Тогда  . Подставив выражения для
. Подставив выражения для  и
и  в исходное уравнение, получим
в исходное уравнение, получим 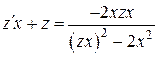 или
или  . Последнее выражение приведем к виду
. Последнее выражение приведем к виду  , т.е.
, т.е.  . Это уравнение с разделяющимися переменными.
. Это уравнение с разделяющимися переменными.
Заменяя  и упрощая правую часть последнего равенства, будем иметь
и упрощая правую часть последнего равенства, будем иметь  ,
,  ,
, 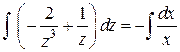 , откуда
, откуда 
 .
.
Окончательно, заменяя  , получим общий интеграл исходного уравнения:
, получим общий интеграл исходного уравнения:  или
или  .
.
2. Линейные неоднородные уравнения. (Линейные дифференциальные уравнения первого порядка). Это уравнения вида
 ,
,  , (1.5)
, (1.5)
где  ,
,  – непрерывные функции на
– непрерывные функции на  .
.
Решение. Решение ищется методом Бернулли, с помощью подстановки  , где
, где  – новая неизвестная функция;
– новая неизвестная функция;  – некоторая функция, значение которой определяется так:
– некоторая функция, значение которой определяется так:
 ; Тогда получаем
; Тогда получаем 
или 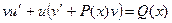 . (1.6)
. (1.6)
Выберем  так, чтобы выражение в скобках обратилось в нуль:
так, чтобы выражение в скобках обратилось в нуль:
 ,
,  . (1.7)
. (1.7)
Решение, полученного для функции  , дифференциального уравнения с разделяющимися переменными:
, дифференциального уравнения с разделяющимися переменными:
 ,
,  ,
,  В виду свободы выбора функции
В виду свободы выбора функции  , можно принять
, можно принять  . Отсюда
. Отсюда
 (1.8)
(1.8)
(1.8) подставим в (1.6).  В результате получим для неизвестной функции
В результате получим для неизвестной функции  уравнение с разделяющимися переменными.
уравнение с разделяющимися переменными.

Его решение позволяет найти исходную неизвестную функцию  .
.
Пример 4. Решить уравнение  .
.
Это уравнение является линейным неоднородным дифференциальным уравнением (ЛНДУ).
Решим его методом Бернулли. Будем считать, что  , тогда
, тогда  ; эти выражения подставим в исходное уравнение
; эти выражения подставим в исходное уравнение
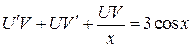 или
или  .
.
Выберем  так, чтобы
так, чтобы  или
или  , откуда
, откуда  . Проинтегрировав обе части последнего уравнения, будем иметь
. Проинтегрировав обе части последнего уравнения, будем иметь  . Возьмем
. Возьмем  , так что
, так что  , значит
, значит  .
.
Выражение  подставим в уравнение
подставим в уравнение  , получим
, получим  или
или  , откуда
, откуда  ,
,  . Интегрируя по частям, найдем
. Интегрируя по частям, найдем  :
:  .
.
В силу того, что  , получим
, получим  и окончательно будем иметь общее решение
и окончательно будем иметь общее решение  .
.

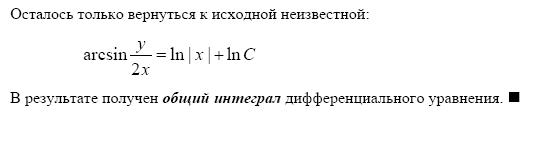
Уравнения Бернулли.
Уравнения вида  называются уравнениями Бернулли.
называются уравнениями Бернулли.

Последнее уравнение является линейным относительно z. Решение его известно. Таким образом, подстановка z=y-n+1 сводит уравнение (2.15) к линейному. На практике ДУ (2.15) удобнее искать методом И. Бернулли в виде y=u•v (не сводя его к линейному).





Дифференциальные уравнения первого порядка. Методы решения.
1. Обыкновенные диф.ур. 1-го порядка
2. Уравнение, разрешенное относительно производной.
3. Общее решение и частное решение.
4. Геометрическая интерпретация диф.ур.
5. Задача Коши для диф.ур.
6. Теорема существования и единственности решения задачи Коши.
7. Уравнения с разделяющимися переменными.
8. Пример 1. Решить уравнение  при начальных условиях
при начальных условиях  .
.
9. Пример 2. Решить уравнение  с начальным условием
с начальным условием 
 .
.
10. Однородные диф.уравнения.
11. Пример 3. Решить уравнение 
12. Линейные неоднородные уравнения.
13. Пример 4. Решить уравнение  .
.
14. Пример 4. Решить уравнение  .
.
15. Уравнения Бернулли
16. Пример 2. Решить уравнение  с начальным условием
с начальным условием 
 .
.




