Многомерная условная оптимизация функций

 

Цель: изучить работу методов многомерной условной оптимизации.

 

Задание:

Для заданной функции найти:

1 Безусловный минимум;

2 Максимальное и минимальное значение в допустимой области поиска, заданной ограничениями x_min ≤ х ≤ x_max и y_min < y < y_max;

3 Построить поверхность отклика и линии уровня функции.

Варианты заданий выбираются в соответствии с таблицей 6.

 

Таблица 6 – Исходные данные для лабораторной работы 6.

№ варианта	Вид функции	a	b	c	xmin	xmax	ymin	ymax
				-	-5
				-	-7
				-
					-4		-7
					-8
							-4
					-2		-7
					-6		-9
				-	-1		-4
				-	-6
				-			-8
					-10		-6
					-1
					-2
							-7
				-	-2
				-	-7
				-	-9
					-5
					-3		-8
					-7		-9
					-5		-2
					-8
							-4
					-2		-7

Вид функции:

1) 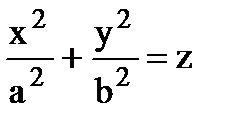– эллиптический параболоид

2) – эллиптический действительный конус

3) 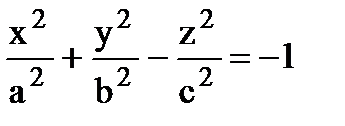– двуполостный гиперболоид

 

 

Перед вставкой функции необходимо задать начальную точку М₀(х₀,у₀),где х₀ = 0,1N; у₀ = 0,3N (N – номер варианта).

 

 

Содержание отчета:

1 Тема лабораторной работы;

2 Цель лабораторной работы;

3 Задание;

4 Текст программы;

5 Результат работы программы;

6 Выводы.

 

Список рекомендуемой литературы

 

1 Бахвалов Н.С. Численные методы. – М.: Наука, 1975. – 275 с.

2 Бажин И.И. Информационные системы менеджмента. – М.: ТУ-ВШЭ, 2000. – 688 с.

3 Березин И.С. Методы вычислений/И.С.Березин, Н.П.Жидков. - М.: Наука, 1966. – 472 с.

4 Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука. Главная редакция физико-математической литературы, 1980. – 518 с.

5 Волков Е.А. Численные методы. – М.: Наука, 1982. – 194 с.

6 Дьяченко В.Ф. Основные понятия вычислительной мате­матики. – М.: Наука, 1977. – 362 с.

7 Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. – М.: Наука, 1982. – 274 с.

8 Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 384 с.

9 Конспект лекций по курсу «Методы оптимизации» (для студентов специальности 7.04030302 очной и заочной формы обучения) / Сост.: Гитис В. Б. – Краматорск: ДГМА, 2011. – 64 с.

10 Крылов В.И. Вычислительные методы/ В.И.Крылов, В.В.Бобков, П.И.Монастырный. – М.: Наука, 1977. – 477 с.

11 Пшеничный Б.Н. Численные методы в экстремальных задачах/ Б.Н.Пшеничный, Ю.М.Данилин. – М.: Наука, 1975. – 420 с.

12 Самарский А.А. Введение в численные методы. - М.: Нау­ка, 1982. – 233 с.

13 Турчак Л.И. Основы численных методов: Учеб. пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 320 с.

14 Численные методы и вопросы организации вычислений / Под. ред. В.П. Ильина, В.Н. Кублановской. – Л.: Наука, 1984. – 184 с.

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

выполнению лабораторных работ

по курсу
«Математические методы исследования операций»

(Методы оптимизации)

 

(для студентов специальности 7.04030302
дневной и заочной формы обучения)

 

Составитель Гитис Вениамин Борисович

 

Редактор Дудченко Елена Александровна

 

 

Подписано в печать ______ Формат 60х84/16

Ризограф. печать Усл. печ. л. Уч.-изд. л.

Тираж ______ экз. ________________________________________________________

ДГМА. 84313, г. Краматорск, ул. Шкадинова, 72