Для нахождения общего решения y’’ +  (x) y’ +
(x) y’ +  (x) y = f (x) необходимо найти частное решение
(x) y = f (x) необходимо найти частное решение  .
.
Его можно найти из общего решения уравнения y’’ +  (x) y’ +
(x) y’ +  (x) y = 0 некоторых вариаций произвольных постоянных
(x) y = 0 некоторых вариаций произвольных постоянных
 =
=  +
+  (5.6)
(5.6)
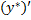 =
=  +
+  +
+  +
+ 
 =
=  +
+  +
+  +
+ 
Подставим в (5.1)
 +
+  +
+  +
+  +
+  (x)
(x)  +
+  +
+
 (x)
(x)  +
+  = f (x)
= f (x)
 +
+  +
+  +
+  +
+  (x)
(x) 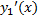 +
+ 
 (x)
(x)  +
+  = f (x)
= f (x)
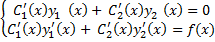
 = W (x)
= W (x)  0
0
 =
= 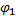 (x)
(x)
 =
=  (x)
(x)
Интегрированием найдем  и
и 
Затем по формуле (5.6) составим общее решение
Теорема (5.2): о наложение решения
Если правая часть уравнения y’’ +  (x) y’ +
(x) y’ +  (x) y = f (x) представляет собой сумму 2-ух функций:
(x) y = f (x) представляет собой сумму 2-ух функций:
f(x) =  (x) +
(x) +  (x),
(x),
а  u
u 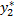 - частное решение уравнения
- частное решение уравнения
 +
+  (x) y ‘ +
(x) y ‘ +  (x) y =
(x) y =  (x)
(x)
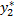 +
+  (x) y ‘ +
(x) y ‘ +  (x) y =
(x) y =  (x)
(x)
То функция 
Является решение данного уравнения
 (
( ) ‘’ +
) ‘’ + 
 ) ‘ +
) ‘ + 
 ) ‘=
) ‘=  ‘’ +
‘’ + 
 +
+ 
 + (
+ (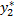 ) ‘’ +
) ‘’ + 
 ) ‘ +
) ‘ + 
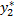 =
=  (x) +
(x) +  (x) = f(x)
(x) = f(x)
10. Уравнение Бернулли. 
11. Уравнение Риккати.:
Уравнение Риккати является одним из наиболее интересных нелинейных дифференциальных уравнений первого порядка. Оно записывается в форме:

где a (x), b (x), c (x) − непрерывные функции, зависящие от переменной x.
Уравнение Риккати встречается в различных областях математики (например, в алгебраической геометрии и в теории конформных отображений) и физики. Оно также нередко возникает в прикладных математических задачах.
Приведенное выше уравнение называется общим уравнением Риккати. Его решение основано на следующей теореме:
Теорема: Если известно частное решение y 1 уравнения Риккати, то его общее решение определяется формулой

Действительно, подставляя решение y = y 1 + u в уравнение Риккати, имеем:

Подчеркнутые члены в левой и правой части можно сократить, поскольку y 1 − частное решение, удовлетворяющее уравнению. В результате мы получаем дифференциальное уравнение для функции u (x):

Второй вариант риккати(писать только один из)

В общем случае не интегрированно в квадратурах
Однако если известно одно частное решение  , то уравнение Риккати можно свести к уравнению Бернулли
, то уравнение Риккати можно свести к уравнению Бернулли
Для этого положим сделаем замену:
y = 
 + p(x)
+ p(x)  + p (x) z + q (x) *
+ p (x) z + q (x) *  + q (x) * 2
+ q (x) * 2  z + q (x)
z + q (x)  = f (x)
= f (x)
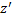 + p(x) z + 2q (x)
+ p(x) z + 2q (x)  z +q(x)
z +q(x)  = 0
= 0
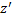 +z (p (x) + 2q (x)
+z (p (x) + 2q (x)  ) + q (x)
) + q (x)  =0
=0
n=2 Бернули
12. Уравнение Лагранжа.:

13. Уравнение Клеро.:


14. Дифференциальные уравнения порядка выше первого. Случаи понижения порядка. 



15. Линейные дифференциальные уравнения n го порядка. Вронскиан. Фундаментальная система решений.:


16. Однородные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение:
Частным случаем рассмотренных выше линейных однородных
дифференциальных уравнений являются ЛОДУ с постоянными
коэффициентами.





17. Линейные неоднородные уравнения. Отыскание частного решения в случае уравнения с квазиполиномом:


Квазиполином Эйлера: Рассмотрим ЛНДУ 2-го порядка с постоянными коэффициентами: y’’ + p y’ + q y = f(x) (5.7) Можно искать частное решение  методом Лагранжа, однако в некоторых случаях
методом Лагранжа, однако в некоторых случаях  можно найти проще Рассмотрим эти случаи:1. f(x) =
можно найти проще Рассмотрим эти случаи:1. f(x) =  ,
,  -многочлен степени n. 2.f(x) =
-многочлен степени n. 2.f(x) =  (
( cos β x +
cos β x +  (x) sin β x). В этих случаях f(x) называют квазиполиномом ЭЙЛЕРА. В этих случаях записывают ожидаемую форму решения
(x) sin β x). В этих случаях f(x) называют квазиполиномом ЭЙЛЕРА. В этих случаях записывают ожидаемую форму решения  с неопределенными коэффициентами и подставляют в ур-е (5.1). Из полученного тождества находят значение коэффициентов. Случай 1: правая часть (5.7) имеет вид:f(x) =
с неопределенными коэффициентами и подставляют в ур-е (5.1). Из полученного тождества находят значение коэффициентов. Случай 1: правая часть (5.7) имеет вид:f(x) =  α
α  R
R  -многочлен степени n. Ур-е (5,7) запишется в виде: y’’ + p y’ + q y =
-многочлен степени n. Ур-е (5,7) запишется в виде: y’’ + p y’ + q y =  (5.8) В этом случае частное реш-е
(5.8) В этом случае частное реш-е  ищем в виде:
ищем в виде:  =
=  Qn (x)
Qn (x)  (5.9) где r – число = кратности α как корня характеристического ур-я
(5.9) где r – число = кратности α как корня характеристического ур-я  + p k + q = 0,т.е. r – число,показывающее сколько раз α явл-я корнем ур-я
+ p k + q = 0,т.е. r – число,показывающее сколько раз α явл-я корнем ур-я  + p k + q = 0, При этом Qn (x) =
+ p k + q = 0, При этом Qn (x) =  +
+  + …. + An –многочлен степени n, записанный с неопределёнными коэффициентами Ai (i= 0, 1, 2,…n) А) Пусть α не является корнем характеристического ур-я:
+ …. + An –многочлен степени n, записанный с неопределёнными коэффициентами Ai (i= 0, 1, 2,…n) А) Пусть α не является корнем характеристического ур-я:  + p k + q = 0,т.е. α
+ p k + q = 0,т.е. α  , r = 0 и решение ищем в виде
, r = 0 и решение ищем в виде  = Q n (x)
= Q n (x)  Б) Пусть α является однократным(простым) корнем характеристического ур-я
Б) Пусть α является однократным(простым) корнем характеристического ур-я  + p k + q = 0, α =
+ p k + q = 0, α =  r = 1,
r = 1,  = x Q n (x)
= x Q n (x)  В) Пусть α =
В) Пусть α =  является 2-хкратным корнем характеристического ур-я
является 2-хкратным корнем характеристического ур-я  + p k + q = 0, r = 2
+ p k + q = 0, r = 2  =
=  Q n (x)
Q n (x)  Случай 2: Правая часть (5.7) имеет вид:f(x) =
Случай 2: Правая часть (5.7) имеет вид:f(x) =  (
( ) cosβx + Q m (x) sin β (x),Где
) cosβx + Q m (x) sin β (x),Где  )и Qm (x) многочлены степени n и m соответственно, α и β - действительного числа, тогда ур-е (5.7) запишется в виде y’’ + py’ + qy =
)и Qm (x) многочлены степени n и m соответственно, α и β - действительного числа, тогда ур-е (5.7) запишется в виде y’’ + py’ + qy =  (
( ) cosβx + Qm (x) sinxβ) (5.10) В это случае частное решение:
) cosβx + Qm (x) sinxβ) (5.10) В это случае частное решение:  =
= 
 * (Ml (x) cosβx + N l (x) sin βx) (5.11) r-число равное кратности (α + βi) как корня уравнения:
* (Ml (x) cosβx + N l (x) sin βx) (5.11) r-число равное кратности (α + βi) как корня уравнения:  + pk + q = 0, Me (x) и Ne (x)-многочлены степени l с неопределёнными коэффициентами. l –наивысшая степень многочленов
+ pk + q = 0, Me (x) и Ne (x)-многочлены степени l с неопределёнными коэффициентами. l –наивысшая степень многочленов  )и Qm (x), l =max(n,m). Замечание 1: После подстановки функции (5.11) в (5.10) приравнивают многочлены, стоящие перед одноименными тригоном. функциями в левой и правой частях ур-я. Замечание 2: Формула (5.11) сохраняется и при
)и Qm (x), l =max(n,m). Замечание 1: После подстановки функции (5.11) в (5.10) приравнивают многочлены, стоящие перед одноименными тригоном. функциями в левой и правой частях ур-я. Замечание 2: Формула (5.11) сохраняется и при  )
) 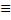 0 и Qm (x)
0 и Qm (x) 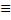 0. Замечание 3: Если правая часть ур-я (5.7) есть сумма функций вида 1 и 2, то для нахождения
0. Замечание 3: Если правая часть ур-я (5.7) есть сумма функций вида 1 и 2, то для нахождения  следует использовать теорему (5.2) о наложении решений. Теорема (5.2): о наложении решений: Если правые части ур-я (5.1) представляют собой сумму 2-х функций:f(x) =
следует использовать теорему (5.2) о наложении решений. Теорема (5.2): о наложении решений: Если правые части ур-я (5.1) представляют собой сумму 2-х функций:f(x) =  (x) +
(x) +  (x),а
(x),а  u
u 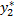 - частные решения ур-я
- частные решения ур-я  +
+  (x) y ‘ +
(x) y ‘ +  (x) y =
(x) y =  (x)
(x)  +
+  (x) y ‘ +
(x) y ‘ +  (x) y =
(x) y =  (x)То
(x)То  является решение данного ур-я. Интегрирование ЛНДУ п-го порядка (n
является решение данного ур-я. Интегрирование ЛНДУ п-го порядка (n  постоянным коэффициентом и правой частью специального вида. Рассмотрим ЛНДУ n-го порядка
постоянным коэффициентом и правой частью специального вида. Рассмотрим ЛНДУ n-го порядка  +
+  (x)
(x)  +
+  (x)
(x)  + … +
+ … +  (x)y = f(x) где
(x)y = f(x) где  (x), …,
(x), …,  (x), f(x) заданы непрерывной функцией на интервале (а, b). Соотв. однородное ур-е
(x), f(x) заданы непрерывной функцией на интервале (а, b). Соотв. однородное ур-е  +
+  (x)
(x)  + … +
+ … +  (x)y = 0. Общее решение y ЛНДУ n-го порядка = сумме частного решения
(x)y = 0. Общее решение y ЛНДУ n-го порядка = сумме частного решения  НУ и общего решения
НУ и общего решения  ОУy=
ОУy=  .
.  может быть найдено если известно общее решение
может быть найдено если известно общее решение  ОУ
ОУ 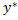 =
=  +
+ 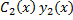 + … +
+ … +  гдеyi(x) – частное реш-е образующее фундаментальную систему решений ОУ.Для нахождения Сi(x)составляется система ур-й
гдеyi(x) – частное реш-е образующее фундаментальную систему решений ОУ.Для нахождения Сi(x)составляется система ур-й  +
+  + … +
+ … +  = 0
= 0  +
+  + … +
+ … + 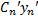 = 0
= 0  +
+  + … +
+ … + 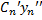 = 0
= 0  +
+ 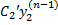 + … +
+ … +  = f (x)Однако для ЛНДУ n-го порядка с постоянными коэффициентами, правая часть f(x) которого имеет специальный вид,
= f (x)Однако для ЛНДУ n-го порядка с постоянными коэффициентами, правая часть f(x) которого имеет специальный вид,  можно найти методом неопределенных коэф-в.Метод подбора частного решения
можно найти методом неопределенных коэф-в.Метод подбора частного решения  для уравнения y’’ +
для уравнения y’’ + 
 + … +
+ … +  y = f (x)
y = f (x) 
 R,где f (x) квазиполином Эйлера тот же что и при n=2.
R,где f (x) квазиполином Эйлера тот же что и при n=2.
18. Линейные неоднородные уравнения. Отыскание частного решения методом вариации произвольных постоянных.:




19. Системы дифференциальных уравнений. Запись задачи в матричной форме:



20. Сведение систем дифференциальных уравнений к одному уравнению более высокого порядка.:









