1. Равноускоренное движение. Пусть в начальный момент времени t=0 материальная точка имеет начальное положение S(0)=0, начальную скорость V(0)=V0 и далее движется прямолинейно с постоянным ускорением a(t)=a. Если S(t) и V(t) – соответственно путь, пройденный точкой за время t, и ее скорость в момент времени t, то S′(t)=V(t) и V′(t)=a(t)=a. Т.е., ф-ция перемещения S(t) явл-ся решением диф.уравнения S′′(t)=a. Найдем решение, интегрируя уравнение дважды.
.
.
2. Уравнение движения. Пусть материальная точка массы m движется прямолинейно под действием переменной силы F(t). Тогда в силу второго закона Ньютона 
. Поскольку a(t)=S′′(t), то ф-ция перемещения S(t) явл-ся решением диф.уравнения 
. Это диф. уравнение называют уравнением движения. Например, если рассматривать свободное падение материальной точки в поле тяготения Земли, то действующая на точку сила сводится к силе тяжести F(t)=P=mg и уравнение движения имеет вид S′′(t)=g. Если полагать, что сила сопротивления воздушной среды пропорциональна скорости движения Fc(t)=kV(t), то суммарная сила, действующая на точку, равна F(t)=mg-Fc(t)=mg−kV(t). В этом случае уравнение движения имеет вид 
. Его решением (для V0=0) явл-ся ф-ция
Скорость и ускорение такого движения изменяются так
3. Геометрические задачи. Пусть требуется найти линию, проходящую ч/з точку А(1,2) и обладающую следующим св-вом: для любой ее касательной отрезок этой касательной, заключенный м/у осями системы координат, в точке касания делится пополам. Обозначим ч/з y(x) уравнение искомой линии и пусть M(x0,y0) - ее произвольная фиксированная точка. Касательная к кривой в этой точке имеет уравнение y-y(x0)=y’(x0)(x-x0). Найдем ординаты точек пересечения этой касательной с осями системы координат.
xB=0, yC=0. Тогда
Т.к М – середина отрезка BC, то
Отсюда 
Т.к. x0 - произвольная точка, то искомая ф-ция должна удовлетворять диф.уравнению первого порядка
Для произвольной постоянной С ф-ция y(x)=C/x удовлетворяет этому уравнению. Т.к. кривая должна проходить ч/з точку А(1,2), то подставив в это решение x=1 и y=2, получим С=2. Решением явл-ся гипербола y=2/x.
2.Диф. уравнения первого порядка: основные определения, задача Коши, общее и частное решения, общий и частный интеграл. Диф. уравнение первого порядка имеет вид 
. (1)
Если (1) представима в виде y’=f(x,y) то ДУ разрешено относительно производной.
Задача Коши. Теорема о существовании и единственности решения ДУ. Если в уравнении y’=f(x,y) ф-ция f(x,y) и ее частная производная 
по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (х0,у0), то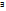 
единственное решение этого уравнения 
, удовлетворяющее условию у0=y(x0).
Геометрический смысл теоремы: через точку (х0, у0) проходит единственная интегральная кривая (решение ДУ).
Условие, что при х = х0 функция у должна равняться заданному числу у0, называется начальным условием.
Общим решением ДУ первого порядка называется ф-ция 
:
1. она удовлетворяет ДУ при любом значении С; 2. 
удовлетворяет условие (х0,у0).
Равенство Ф(х,у,С)=0 называется общим интегралом ДУ.
Частным решением называется любая ф-ция 
которая получается из общего решения 
, если в последнем произвольному постоянному С придать определенное значение С=С0. Соотношение Ф(х,у,С0)=0 называется частным интегралом ДУ.
3.ДУ первого порядка: понятие изоклины, особые точки ДУ. Геометрическая интерпретация общего решения ДУ.
Особым решением называется такое решение ДУ, во всех точках которого нарушены условия теоремы Коши, т.е. в любой окрестности каждой точки (х,у) особого решения 
, по крайней мере, две интегральные кривые, проходящие через эту точку.
Геометрическая интерпретация ДУ первого порядка. Пусть дано ДУ, разрешенное относительно производной: y’=f(x,y) (1')
и общее решение данного уравнения. Общее решение определяет семейство интегральных кривых на плоскости Оху.
Уравнение (1') для каждой точки М(х,у) определяет знание производной 
, т.е. угловой коэффициент касательной к интегральной кривой, проходящей ч/з эту точку. Т.о., ДУ (1') определяет поле направлений на плоскости Оху.
С геометрической точки зрения задача интегрирования ДУ заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля в соответствующих точках. Для геометрическое место точек, в которых выполняется соотношение 
называется изоклиной ДУ.
4.ДУ с разделяющимися переменными. Метод решения. Пример. ДУ вида р(x)dx+q(y)dy=0 называют уравнением с разделенными переменными.
Р(х)+Q(у)=С - общий интеграл ДУ разделенными переменными.
Уравнение вида
М1(х) N1(у) dx + М2(х) N2(y)dy = 0 называется уравнением с разделяющимися переменными, где М1, М2 непрерывна на [a,b], N1, N2 непрерывна на [c,d]. Если N1(у0)=0, то у=у0 - решение уравнения. Аналогично, если М2(х0)=0, то х=х0 - решение уравнения. Если N1(у)М2(х)≠0, то уравнение равносильно
являющемуся уравнением с разделенными переменными.
Интегрируем это уравнение:
– общий интеграл
Пример.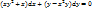 
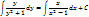
5.Однородные и приводящиеся к однородным ДУ I порядка. Метод решения. Пример. Ф-ция f(x,у) называется однородной ф-цией n -го измерения относительно переменных х и у, если при любом λ справедливо тождество
.
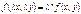Если 
, то f(x,у) однородная нулевого измерения.
Пример.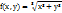 
. f(x,у) - однородная нулевого измерения.
Уравнение 1-го порядка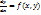 
называется однородным относительно х и у, если ф-ция f(x,у) есть однородная ф-ция нулевого измерения относительно х и у.
Перепишем ДУ в виде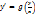 
Замена: y=Ux, где U=U(x), тогда 
, тогда уравнение примет вид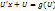 
=g(U)-U
Если 
, то 
- решение ДУ. Если U 
, то
интегрируем
.
Если Ф(U) - первообразная для 
, то общий интеграл имеет вид
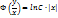
Уравнения вида
при 
приводятся к однородным подстановкой x=u+ 
, y= 
, где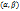 
- точка пересечения прямых 
и 
Если 
, то подстановка 
позволяет разделить переменные.
Пример. 
Замена: y=Ux,
; 
;
; 
; 
; 
.
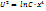
6.Линейные ДУ I порядка, уравнения Бернулли. Методы решения. Примеры. Линейным уравнением первого порядка называется уравнение вида
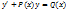
линейное относительно неизвестной функции и ее производной, при этом ф-ции Р(х) и Q(x) непрерывны на некотором интервале (а,b).
Метод Бернулли. Решение уравнения ищем в виде: y=uv, где u=u(x), v=v(x), тогда y’=u’v+uv’. Выполним подстановку: u’v+uv’+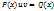 
1) 
; 
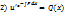
Пример. 
1) 
; 
; 
; 
; 
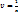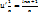Метод вариации произвольного постоянного.
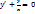- однородное у-ие соотв-щее
; 
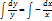
Подставим в исходное уравнение:
, тогда 
Уравнение Бернулли -уравнение вида
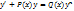
где Р(х) и Q(х) - непрерывные на некотором интервале (а,b), 
Разделим на 
(#)
Обозначим 
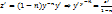
Подставим в (#)
- линейное уравнение относительно z.
Пример.
, получим
- линейное уравнение.
Решим методом Бернулли.
z=uv;z=u’v+uv’, тогда
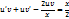
1) 
; 
; 
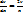
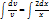
2) 
)
7.ДУ в полных дифференциалах. Методы интегрирования. Примеры. Уравнение M(x,y)dx+N(x,y)dy=0 (1) называется уравнением в полных дифференциалах, если М(х,у) и N(х,у) - непрерывно-дифференцируемые в области D ф-ции, для которых выполняется соотношение
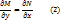
Докажем, что если левая часть уравнения (1) есть полный дифференциал, то выполняется условие (2), и обратно - при выполнении условия (2) левая часть уравнения (1) есть полный дифференциал некоторой функции u(x,у), т.е. уравнение (1) имеет вид du(x,y)=0 u(х,у) = С.
Предположим
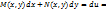
Тогда
Дифференцируя первое соотношение по у, а второе - по х, получим:
.
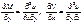Равенство (2) является необходимым условием для того, чтобы левая часть уравнения (1) была полным дифференциалом некоторой функции u(х,у). Достаточность: 
,
где х0 - абсцисса любой точки из области существования решения. Дифференцируем по у:
.
,
.
Т.о., ф-ия u(х,у) будет иметь вид:
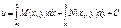Общий интеграл имеет вид:
(x0,y0) – точки, в которых M и N определены.
Пример.
1) 
Проверим условие
или
2) 
тогда
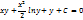
8. ДУ высших порядков, допускающие понижение порядка вида. ДУ n-го порядка имеет вид:
. (*)
Выразим из (*) y(n)
1). 
Найдем общий интеграл этого уравнения. Интегрируя по х левую и правую части, получим:
.
Интегрируем:
2) 
не содержит у.
Подстановка 
, тогда уравнение примет вид:
Рассмотрим ДУ 2-го порядка разрешенного относительно y’’ этого вида.
. Подстановка 
. Получим: 
.
Пусть найдено решение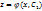 
, тогда 
3) 
не содержит x.
Подстановка 
и т.д.
Рассмотрим уравнение 2-го порядка этого вида 
. Подстановка 
. Получим:
.
Пусть найдено решение 
, тогда 
,
, где 
– первообразная 
9. Линейные ДУ высших порядков: основные определения, постановка задачи Коши.
11.Неоднородные ДУ II порядка: теорема о структуре общего решения.
Пусть имеем неоднородное линейное уравнение второго порядка
(1)
Теорема о структуре общего решения 1. Общее решение неоднородного уравнения представляется как сумма какого-нибудь частного решения этого уравнения у* и общего решения 
соответствующего однородного уравнения
(2)
Док-во. Доказать, что сумма
(3) - общее решение неоднородного уравнения.
Подставим 
в уравнение (1) вместо у:
(4)
Т.к. - решение уравнения (2), то
Т.к. у* - решение уравнения (1),
, равенство (4) является тождеством. Т.о. первая часть теоремы доказана.
Докажем, что выражение (3) - общее решение уравнения (1), т.е. докажем, что входящие в него произвольные постоянные можно подобрать так, чтобы удовлетворялись начальные условия: 
каковы бы ни были числа x0, у0 и 
(x0 должно быть взято из области, где функции a1, а2, f(x) непрерывны).
Представим 
где 
и у2 - линейно независимые решения уравнения (2), C1, С2 - произвольные постоянные. Перепишем равенство (3) в виде 
Тогда на основании начальных условий 
Из этой системы уравнений нужно определить С1 и С2.
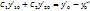
Определитель этой системы - определитель Вронского для функций y1 и у2 в точке х=х0. Т.к. эти ф-ции по условию линейно независимы, то определитель Вронского 
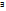такие значения C1 и С2, при которых формула (3) определяет решение уравнения (1), удовлетворяющее данным начальным условиям. Теорема доказана.
12.Линейные однородные ДУ II порядка с постоянными коэффициентами: характеристичес-кое уравнение, вид общего решения. Имеем линейное однородное уравнение 2-го порядка
(*)
где р и q - постоянные действительные числа. Найдем частные решения в виде
у = еkх, где k = const; тогда
Подставим в уравнение (*):
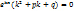
Т.к. 
, то,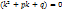 
- характеристическое уравнением по отношению к уравнению (*).
Характеристическое уравнение есть квадратное уравнение, имеющее два корня: обозначим их k1 и k2.
Возможны следующие случаи:
I. k1 и k2 – действительные,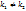 
;
частные решения: 
Эти решения линейно независимы, т.к.
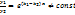
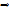общее решение имеет вид 
II. k1 и k2 - комплексные числа;
Частные решения:
Общее решение:
(#)
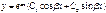Рассмотрим случай, когда корни характеристического уравнения чисто мнимые. При р=0, уравнение (*) имеет вид 
Характеристическое уравнение принимает вид 
Корни характеристического уравнения
.
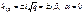Решение (#) принимает вид
III. k1 и k2 - действительные равные числа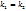 
.
Частные решения: 
, 
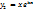
Общее решение: 
.
13.Линейные неоднородные ДУ II порядка с постоянными коэффициентами: нахождения частного решения подбором по виду правой части уравнения. Пусть имеем уравнение
(*)
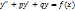где р и q - действительные числа.
Нахождение частного решения подбором по виду правой части уравнения. Если правая часть уравнения имеет следующий вид:
, где α и β - постоянные, Рn(х) и Qm(х) - многочлены от х соответственно n -й и m -й степени, тогда частное решение уравнения имеет вид:
r = показателю кратности корня 
в характеристическом уравнении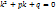 
; Rl(х) и Tl(x) - полные многочлены от х степени l с неопределенными коэффициентами, 
.
.
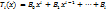Частные случаи f(x):
1) 
2) 
, A – постоянная 
3) 
4) 
5) 
6) 
, 
.
Рассмотрим первый частный случай: 
. Тогда возможны следующие случаи:
а) Число α не является корнем характеристического уравнения
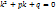. Тогда частное решение нужно искать в виде:
Дифференцируем:
Подставим в (*):
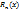- многочлен степени n
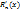- многочлен степени n-1
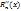- многочлен степени n-2
Т.о., слева и справа от знака равенства стоят многочлены n -й степени. Приравнивая коэффициенты при одинаковых степенях х (число неизвестных коэффициентов = n+1), получим систему n+1 уравнений для определения неизвестных коэффициентов А0, А1, А2,..., Аn.
б) Число α есть простой корень характеристического уравнения.
в) Число α - двукратный корень характеристического уравнения.
14. Системы ДУ: основные определения, система ДУ нормального типа, постановка задачи Коши. Ф-ии у1=у1(х), у2=у2(х), …, уn=уn(х) -удовлетворяют системе ДУ, содержащих аргумент х, искомые ф-ции у1, у2, …, уn и их производные.
Рассмотрим систему уравнений первого порядка:
- система нормального типа. Проинтегрировать систему - значит определить ф-ции у1, у2, …, уn, удовлетворяющие системе уравнений нормального типа и данным начальным условиям:
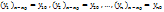
Рассмотрим нормальную систему трех уравнений с тремя неизвестными функциями: х=х(t), у=у(t), z=z(t).
Зададим начальные условия: 
.
Дифференцируем по t первое из уравнений:
Заменим производные их выражениями f1, f2, f3 из уравнений (*):
Дифференцируем и аналогично предыдущему, найдем:
Запишем систему:
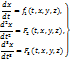
Определим ф-ии у =у(t), z=z(t), выразив их через х, t и производные 
:
(#)
Подставим эти выражения в последнее из уравнений, получим уравнение 3-го порядка для определения х=х(t):
.
Дифференцируя последнее выражение 2 раза, найдем производные как ф-ции от t, С1, С2, С3.
Подставляя эти ф-ии в уравнения (#), определим у(t), z(t):
Рассмотренный метод решения нормальных систем называется методом исключения.
Теорема Коши.
Пусть функции 
, i =1, 2, 3 непрерывны по всем переменным в некоторой области D и имеют в этой области непрерывные частные производные:
. Тогда каковы бы ни были значения 
единственное решение системы 
, удовлетворяющее начальным условиям
.
