| № ветви | |||
| 33.792 | 6.865 | 22.456 |
| D(I),A | 43.99 | 0.302 | 3.785 |
| Imax,A | 50.37 | 8.238 | 27.32 |
1.4. Вероятностные характеристики аргумента
комплексной случайной величины параметра режима
Для полной характеристики комплексного значения тока нагрузки в любой ветви электрической сети в ряде случаев недостаточно знать модуль, необходимо хотя бы приближенно оценить аргумент. Если в качестве основной характеристики комплексной случайной величины (тока нагрузки) считать модуль, то числовые характеристики аргумента полного тока следует вычислять как условное математическое ожидание и дисперсию.
Тогда математическое ожидание случайной величины j (аргумента) относительно значения I составит
.
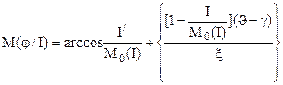Дисперсия аргумента:
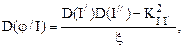
где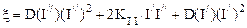 
;
;
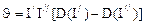Диапазон практически возможных значений аргумента при условии, что ток равен максимальному, определится из неравенства
Чем ближе значения расчетного тока и его математического ожидания, тем с большей точностью можно пользоваться приближенной формулой для определения математического ожидания аргумента
.
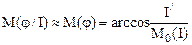2. Расчет потерь мощности
при вероятностном задании нагрузки
Полная мощность, теряемая в каждом элементе схемы сети, вычисляется по формуле
.
Вероятностные характеристики потерь мощности зависят от числовых характеристик квадрата полного тока.
Математическое ожидание квадрата тока, независимо от условий, определяется как:
.
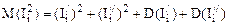Дисперсию квадрата полного тока в рамках корреляционной теории при произвольных функциях распределения можно вычислить с достаточной точностью лишь при условии относительно небольших вариаций действительной и мнимой составляющих:
С учетом выше изложенного, математическое ожидание потерь мощности
а максимальное значение
,
где D(DSi) – дисперсия потерь мощности, которая определяется по выражению
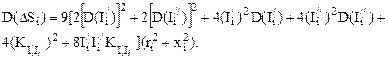Математическое ожидание суммарных потерь мощности во всех элементах сети
Ввиду второстепенного значения дисперсии потерь мощности для практических расчетов дисперсия суммарных потерь мощности приближенно определится без учета вероятностных связей:
.
Суммарные потери мощности являются функцией случайных коррелированных векторов нагрузки ветвей, которые характеризуются корреляционной матрицей.
Тогда максимально возможные потери мощности во всей сети
,
где b=2¸3 в зависимости от требуемой степени надежности получаемого результата.
3. Определение потерь электроэнергии
при вероятностном задании нагрузки
Потери электроэнергии, обусловленные нагрузочными токами, в любом элементе электрической сети можно определить из выражения
,
где ri – активное сопротивление элемента; 0-Т – интервал времени, за который рассчитываются потери энергии.
При вероятностно-статистическом характере электропотребления на интервале 0-Т нагрузки обычно задаются числовыми вероятностными характеристиками. Поэтому целесообразно потери электроэнергии выразить также в функции этих характеристик.
Потери электроэнергии в элементе сети определятся по формуле
,
а суммарные потери электроэнергии во всех элементах электрической сети
.
Пример 3.
Используя исходные данные примеров 1 и 2 и рис.1.1, необходимо определить вероятностные характеристики потерь мощности. Рассчитать максимальные потери мощности и электроэнергии за год во всей сети.
Решение:
Математическое ожидание потерь мощности в трех фазах для первой ветви
Дисперсия потерь мощности при произвольных функциях распределения действительной и мнимой составляющих для первой ветви
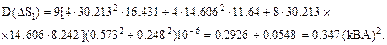Максимальное значение потерь мощности при b=2.5
Результаты расчетов для остальных ветвей приведены в табл. 1.3.
Таблица 1.3
