М.К. Сальникова
ВЕРОЯТНОСТНЫЕ И СТАТИСТИЧЕСКИЕ ЗАДАЧИ ЭЛЕКТРОСНАБЖЕНИЯ
РАСЧЕТ ПОТЕРЬ МОЩНОСТИ И ЭНЕРГИИ
В ЭЛЕКТРИЧЕСКОЙ СЕТИ ПРИ ВЕРОЯТНОСТНОМ ЗАДАНИИ НАГРУЗКИ
Методические указания по выполнению контрольной
работы для студентов специальности
10.04 «Электроснабжение промышленных предприятий»
всех форм обучения
Братск 2002
Вероятностные и статистические задачи электроснабжения. Расчет потерь мощности и энергии в электрической сети при вероятностном задании нагрузки: Методические указания /
М.К. Сальникова. – Братск: БрГТУ, 2002. - 19 с.
Методические указания предназначены для выполнения контрольной работы по дисциплине «Вероятностные и статистические задачи электроснабжения» студентами, обучающимися по специальности «Электроснабжение промышленных предприятий». Содержат варианты заданий, подробные пояснения и примеры по расчету потерь мощности и энергии в электрических сетях при вероятностном задании нагрузки.
Рецензент В.Г. Курбацкий, д-р. техн. наук, профессор кафедры СЭС
Печатается по решению издательско-библиотечного совета
665709, Братск, ул. Макаренко, 40
Братский государственный технический ун-т
Тираж 150 экз. Заказ
СОДЕРЖАНИЕ
Введение........................................................................... 4
1. Интегральные характеристики режимов сложных электрических сетей 5
1.1. Расчет интегральных характеристик режимов с использованием комплексных случайных величин.................................................................................... 6
1.2. Расчет интегральных характеристик действительных и мнимых составляющих параметров режимов............................................................................. 7
1.3. Вероятностные характеристики модуля комплексной случайной величины параметра режима........................................................................................ 10
1.4. Вероятностные характеристики аргумента комплексной случайной величины параметра режима.................................................................................... 12
2. Расчет потерь мощности при вероятностном задании нагрузки 13
3. Определение потерь электроэнергии при вероятностном задании нагрузки 14
4. Задание на контрольную работу................................ 17
Список рекомендуемой литературы.............................. 20
ВВЕДЕНИЕ
Каждое явление окружающего нас мира, в том числе и явление, происходящее в электроэнергетической системе при производстве, передаче, распределении и потреблении электроэнергии, связано с бесконечным множеством других явлений более или менее тесными взаимосвязями.
Изучение случайных явлений необходимо начинать с выявления закономерностей в них самих, при этом количественная оценка возможна на основе использования методов математической статистики и теории вероятностей. Эти методы, не определяя воздействие каждого отдельного фактора или их группы на случайное явление, дают возможность охарактеризовать результирующее воздействие всех факторов в их сочетаниях и изменчивости. Однако следует иметь в виду, что вероятностно-статистические методы не должны трактоваться как описание реального изменения изучаемого явления, хотя и имеют отношение к нему. Как и всякий статистический метод, рассматриваемые методы являются математическим описанием того, что мы можем знать о физическом явлении, и служат для представления статистических предсказаний относительно результатов измерений, которые можно произвести на изучаемом объекте.
Область применения вероятностных методов в энергетике непрерывно расширяется на этапе проектирования и эксплуатации электрических систем. Почти все вопросы, возникающие на данных этапах, в том числе и вопросы практической реализации на основе интегральных характеристик режимов и надежности, должны решаться с использованием технико-экономических показателей.
Вероятностные методы позволяют количественно оценить частоту появления тех или иных условий. Применение вероятностных методов, базирующихся на достаточно надежных статистических данных, способствует уменьшению числа экономически нецелесообразных решений.
Задачей вероятностных и других методов математики в решении прикладных технических задач является преобразование исходной информации в форму, удобную для принятия практических решений.
Интегральные характеристики режимов сложных электрических сетей
В общем случае конфигурация схемы электрических соединений и параметры ее элементов, при рассмотрении на достаточно длительных интервалах времени, являются случайными вследствие влияния большого числа случайных факторов на характеристики системы (отказы и преднамеренные отключения оборудования, влияние внешних температурных и погодных условий и т.д.). Нагрузки потребителей систем электроснабжения также отличаются значительной изменчивостью.
С вероятностно-статистической точки зрения наиболее полную информацию о параметрах режимов дают функции распределения, в общем случае многомерные (дифференциальные или интегральные). Однако в настоящее время информация о функциях распределения узлов нагрузки, как правило, отсутствует. Поэтому для решения большей части практических задач достаточно ограничиться определением числовых вероятностных характеристик в рамках корреляционной теории, т.е. математических ожиданий, дисперсий, средних квадратических отклонений и корреляционных моментов, предполагая известным вид закона распределения, который можно установить из качественного анализа сети и законов распределения нагрузок потребителей.
Для определения вероятностных характеристик параметров режимов (нагрузок ветвей I и напряжений узлов U) относительно базового целесообразно использовать обобщенные параметры схем: матрицы узловых сопротивлений Z, коэффициентов распределения C, собственных и взаимных проводимостей Y и матрицы распределения напряжений ветвей Д.
Нагрузки ветвей I и напряжения узлов U определяются из уравнений

где  и
и  - мгновенные случайные величины нагрузок узлов и ЭДС ветвей.
- мгновенные случайные величины нагрузок узлов и ЭДС ветвей.
В общем случае случайные векторы и обобщенные параметры сети являются комплексными.
1.1. Расчет интегральных характеристик режимов
с использованием комплексных случайных величин
Для определения интегральных характеристик режимов в неоднородных сетях с низкой степенью компенсации реактивной мощности целесообразно использовать модель системы комплексных случайных величин.
При расчетах режимов электрических сетей возникает необходимость определения числовых характеристик суммы (если сеть разомкнутая) или линейной комбинации случайных величин (если сеть замкнутая).
Пусть


Математическое ожидание величины zk

Тогда корреляционный момент между zk и zl запишется в виде
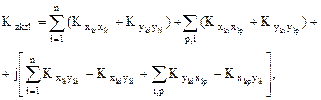
где р=1..n и р¹i.
При l=k мнимая часть  равна нулю и корреляционный момент равен дисперсии комплексной случайной величины:
равна нулю и корреляционный момент равен дисперсии комплексной случайной величины:
 .
.
Выдвигая гипотезы о видах законов распределения для указанных параметров режимов, можно определить все необходимые вероятностные характеристики. Наиболее часто исходные нагрузки узлов и ЭДС ветвей аппроксимируют нормальным законом распределения.
1.2. Расчет интегральных характеристик действительных
и мнимых составляющих параметров режимов
Целью расчета интегральных характеристик режимов является определение числовых вероятностных характеристик модуля и аргумента тока, мощности, напряжения. Эти характеристики являются функцией соответствующих активной и реактивной составляющих, поэтому возникает необходимость получения их для электрических сетей произвольной конфигурации.
Для сокращения громоздких математических преобразований будем считать, что свободные ЭДС в ветвях отсутствуют. При этом уравнение связи между токами нагрузок узлов и ветвей будет иметь вид

Модули и аргументы комплексных значений токов в ветвях, а также напряжений узлов следует определять как функции случайных величин действительных и мнимых составляющих. Следовательно, целью расчета интегральных характеристик режимов в рамках корреляционной теории является определение математических ожиданий и дисперсий действительных и мнимых составляющих токов в ветвях и напряжений в узлах, а также корреляционных моментов между ними при известных числовых характеристиках исходных нагрузок.
Тогда матрицы математических ожиданий действительных I/ и мнимых I// составляющих полного тока ветвей равны

Вычисление вероятностных характеристик в ветвях значительно упрощается, если сеть обладает высокой степенью однородности параметров. Мнимая часть матрицы коэффициентов распределения по сравнению с действительной будет очень мала. Тогда расчеты выполнятся по приближенным формулам


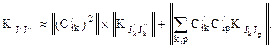
Пример 1.
Рассчитать математические ожидания, дисперсии и корреляционные моменты токов нагрузок в ветвях (рис.1.1), если известны вероятностные характеристики исходных нагрузок узлов. Сопротивления проводов приведены в табл. 1.1.

 ;
;
 ;
;
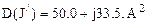 ;
;
 .
.
 ;
;
 ;
;  ;
;  .
.
Коэффициенты распределения схемы
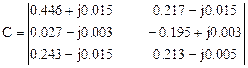 .
.
Таблица 1.1
Сопротивления проводов
| № участка | |||
| Активное сопротивление, Ом | 0.573 | 0.325 | 0.673 |
| Реактивное сопротивление, Ом | 0.248 | 0.159 | 0.296 |
Решение:
Запишем значения мгновенных случайных величин действительных и мнимых составляющих нагрузок узлов в виде следующих матриц:
 ;
; 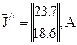 ;
;  ;
; 
Тогда, убрав диагональные элементы, корреляционные матрицы между действительными и мнимыми составляющими токов нагрузок можно представить в виде столбцовых матриц:
 ;
;  ;
; 
Математические ожидания токов нагрузок ветвей
 ,
,
где  ;
;


Дисперсии и корреляционные моменты токов нагрузок в ветвях равны

где  ;
;
 ;
;
 ;
;
 ;
;
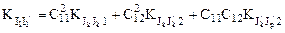 ;
;






