Алгоритм упорядкування елементів одновимірного масиву.
Розглянемо невпорядкований набір з шести чисел: 3, 5, 6, 4, 2, 1. Ці числа введемо в одновимірний масив.
Завдання. Упорядкувати елементи масиву за зростанням (1, 2, 3, 4, 5, 6) або за спаданням (6, 5, 4, 3, 2, 1) значень.
Метод обміну.
Складемо алгоритм упорядкування елементів цього масиву за зростанням методом обміну, який інакше називають методом «бульбашки». Цей метод полягає в наступному:
розглядають першу пару елементів масиву. Якщо перший елемент більший, ніж другий, то їх міняють місцями. Другий елемент порівнюють з третім і, якщо потрібно, застосовують обмін, і т. ін. — максимальний елемент (тут 6) розташується в кінці масиву, тобто там, де потрібно (порівняння: максимальний елемент переміщується в кінець масиву подібно до бульки, яка, збільшуючись, випливає на поверхню під час кипіння води в чайнику). Після цього знову розглядають масив, але вже без останнього елемента, і застосовують до нього метод обміну — другий за величиною елемент (тут 5) опиниться в масиві на передостанній позиції і т. ін. Якщо масив має n елементів, то метод треба застосувати n - 1 разів кожного разу до меншої кількості елементів. Упорядковані елементи будуть нагромаджуватися в кінці масиву.
Наведемо словесний опис алгоритму розв'язування задачі
1. Порівняти перший елемент з другим. Якщо перший елемент більший, то поміняти їх місцями.
2. Порівняти другий елемент з третім. Якщо другий більший, то поміняти їх місцями і т. ін.
Після такого процесу найбільший елемент розташується в кінці масиву, але попередні елементи ще не будуть упорядковані. Тому треба
3. Повторити пункти 1-2 для п'яти перших елементів.
4. Повторити пункти 1-2 для чотирьох перших елементів.
5. Повторити пункти 1-2 для трьох перших елементів.
6. Повторити пункт 1 для двох перших елементів.
Розгляньте блок-схему даного алгоритму та його запис на навчальній алгоритмічній мові (НАМ) та мові Паскаль.
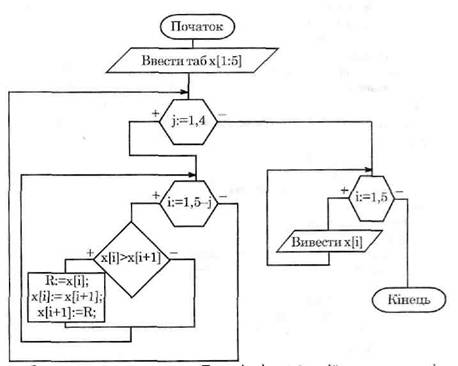
Запишемо даний алгоритм.
Тут змінні R, x[i] — дійсного типу, а змінна і — цілого типу.
програма sort_bubl;
змінні і: цілі;
R: дійсні;
x: масив[1..5] із дійсні;
Початок
для і:=1 до 5 виконати
Початок
вивести(' Введіть ',і,'-й елемент');
ввести(х[і])
кінець;
для j:=1 до 4 виконати
для i:=1 до 5-j виконати
якщо x[i]> x[i+1] то
Початок
R:=x[i];
x[i]:= x[i+1];
x[i+1]:=R
кінець;
для i:=1 до 5 виконати
вивести (x [i])
Кінець.
Перекладемо цей алгоритм мовою Паскаль.
program Sort;
const n = 7;
а: array [l..n] of integer = (75, 34, 18, 56, 45, 64, 23);
var і, j: integer;
dop: integer;
Begin
for j:= 1 to n - 1 do
for і:= 1 to n - j do
if a[i] > a[ i+1 ] then
Begin
dop:= a[i+1]; a[i+1]:= a[i]; a[i]:= dop
end;
writeln('виводимо результати');
for і:= 1 to n do write(a[i]: 4)
End.
Виконаємо програму.
Розглянемо зовнішній цикл. Спочатку j:= 1. Після виконання внутрішнього циклу (для і від 1 до 6) масив буде таким: 34, 18, 56, 45, 64, 23, 75.
Далі матимемо:
j:=2. Виконаємо внутрішній цикл. Отримаємо: 34, 18, 56, 45, 23, 64, 75.
j:=3. Виконаємо внутрішній цикл. Отримаємо: 34, 18, 45, 23, 56, 64, 75.
j:=4. Виконаємо внутрішній цикл. Отримаємо: 34, 18, 23, 45, 56, 64, 75.
j:=5. Виконаємо внутрішній цикл. Результат: 18, 23, 34, 45, 56, 64, 75.
j:=6. Виконаємо внутрішній цикл. Результат: 18, 23, 34, 45, 56, 64, 75.
Наведені числа можна впорядкувати і без алгоритму та комп'ютера.
Практичне значення створеного алгоритму полягає в тому, що він є масовим. Його можна використати для впорядковування великої кількості чисел чи складніших даних: прізвищ, імен тощо.
Наприклад, замість чисел можна розглядати імена:
Наталка, Ростик, Тарас, Юля, Роман, Галя, Андрій.
Уявіть, що імен є багато. Впорядкувати їх за алфавітом «уручну» вженепросто. А алгоритм виконає це. Потрібно лише у програмі замінити в описах тип данихinteger на string ось так:
const n = 7;
а: array [1..n] of string =('Наталка', 'Ростик', 'Tapac', 'Юля', 'Роман', Таля', 'Андрій');
var і, j: integer; c: string;
Виконаємо програму і отримаємо результат:
Андрій Галя Наталка Роман Ростик Тарас Юля.
Довідка. Щоб упорядкувати елементи масиву за спаданням, треба знак нерівності в логічному виразі поміняти на протилежний, тобто повинно бути так: a[i] <a[i+l].
Інші методи впорядкування масивів.
Окрім алгоритму впорядкування масиву методом обміну, є чимало інших методів упорядкування. Найпростіший (але найтриваліший) — це метод мінімальних елементів. Цей метод полягає в такому: розглядають увесь масив, визначають мінімальний елемент та його номер і міняють його місцями з першим елементом. Розглядають масив без першого елемента. Застосовують до нього метод і так n -1 разів. Упорядковані елементи будуть поступово переноситися на початок масиву.
Інший метод упорядкування — метод вставки. У цьому випадку розглядають увесь масив, і перший елемент порівнюють з іншими, доки не знайдуть меншого від нього. Перша позиція в масиві стає позицією вставки. Знайдений менший елемент і його індекс запам'ятовують. Усі елементи масиву, починаючи від позиції вставки до того, що передує знайденому, зміщують праворуч. Значення знайденого елемента записують у позицію вставки і порівнюють його з елементами, що залишилися. Якщо буде виявлено ще менший елемент, то повторюють процедуру вставки і так доти, доки не дійдуть до кінця масиву — лише після цього перший елемент буде на місці. Розглядають масив без першого елемента і застосовують до нього описаний метод і т.п.
Обидва описані алгоритми вважаються простішими, ніж метод обміну, але менш ефективними, оскільки потребують більшої кількості операцій.
Завдання. Застосуйте описані алгоритми до деякого заданого набору цілих чисел, наприклад, 10, 15, 5, 7, 14, 1.
Відшукання елемента із заданою властивістю методом бісекції.
Нехай в одному масиві (з іменем а) є імена учнів: Наталка, Ростик, Тарас, Роман, Галя, Андрій, Юля, а в масиві b в такому ж порядку є номери їхніх телефонів. Як найшвидше можна дізнатися, який номер телефону в Галі? Тут відповідь видно відразу — це значення 5-го елемента масиву b, тобто b[5].Однак насправді імен ми не бачимо, бо вони є в пам'яті комп'ютера. Та й імен може бути дуже багато (сотні й тисячі).
Таку задачу розв'язують методом бісекції— послідовного ділення масиву навпілза таким алгоритмом:
1. Масив а треба спочатку впорядкувати, одночасно і відповідно так само міняючи місцями елементи масиву b. Упорядкований масив а матиме вигляд(ми його не бачимо):
Андрій Галя Наталка Роман Ростик Тарас Юля
2. У масиві є сім елементів. Вибираємо середній: a[4].
3. Якщо a[4] = 'Галя' (а це не так), то відповідь b[4] і стоп.
4. Якщо a[4] < 'Галя' (а це не так), то беремо праву частину масиву:
5 6 7
Ростик Тарас Юля,
інакше (це так) - ліву:
1 2 3
Андрій Галя Наталка.
5. Визначаємо і вибираємо середній елемент a[2].
6. Якщо a[2] = 'Галя' (а це так), то відповідь b[2] і стоп, інакше — пошук продовжити.
Кажуть, що потрібний елемент відшукано за дві операції вибирання (читання) елементів масиву а.
Висновок. Якби масив був невпорядкований, то значення 'Галя' вньому ми б відшукали за п'ять операцій читання. Використовуючи алгоритм поділу впорядкованого масиву навпіл, задачу розв'язано за допомогою двох операцій читання. Економія ресурсів виконавця (часу розв'язування задачі) суттєва. Ось чому перед пошуком інформації дані треба впорядковувати.






