Средняя величина – это обобщающая характеристика однородной совокупности явлений по определенному признаку. Все многообразие средних величин и способы их расчета можно представить в виде схемы (рис.2).
Рис.2. Виды средних величин
Средняя арифметическая простая и взвешенная применяется, если имеется несколько различных индивидуальных значений одного и того же признака.
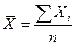(1)
или
(2)
Формула (1) применяется для несгруппированных данных, формула (2) для сгруппированных.
Средняя геометрическая применяется, если необходимо определить среднее значение коэффициентов (темпов) роста, если данные представлены в виде геометрической прогрессии.
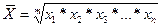, где
х I – коэффициенты (темпы) роста.
Средняя квадратическая рассчитывается в случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций.
Мода – значение признака, наиболее часто встречающегося в исследуемой совокупности. Для интервальных вариационных рядов мода определяется в 2 этапа:
1) определение модального интервала – интервала с наибольшей частотой;
2) определение моды по формуле:
3)
,
где Хмо - нижняя граница модального интервала; iмо – величина модального интервала; fмо – частота модального интервала; fмо-1 – частота интервала, предшествующего модальному; fмо+1 – частота интервала, следующего за модальным.
Медиана – значение признака, приходящееся на середину ранжированной совокупности.
Определение медианы осуществляется в 2 этапа:
1) Нахождение медианного интервала. Для определения медианного интервала необходимо подсчитать накопленные частоты ряда. Медианным является интервал, которому соответствует накопленная частота, превышающая полусумму частот ряда, а предыдущая накопленная частота должна быть меньше полусуммы частот ряда.
2) Медиана интервального ряда распределения определяется по формуле:
,
где Хме – нижняя граница значения интервала, содержащего медиану; iме – величина медианного интервала; Σf – сумма частот ряда распределения; Sме-1 – сумма накопленных частот, предшествующих медианному интервалу; ƒме - частота медианного интервала.
Вариация – это изменение значений какого-либо признака у отдельных единиц статистической совокупности в один и тот же момент времени.
Величина вариации признака в статистической совокупности характеризует ее однородность.
В статистической практике для изучения и измерения вариации используются следующие показатели:
- размах вариации (R)
R = Xmax – Xmin,
где Xmax – наибольшее значение варьирующего признака;
Xmin – наименьшее значение признака.
- среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признака от их средней.
- если данные представлены в виде отдельных значений признака (несгруппированы):
 |
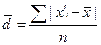- в случае наличия частот в ряду распределения:
 |
где n – число единиц наблюдения; fi – частота интервала; x`i – среднее значение в интервале вариационного ряда; 
- общая средняя ряда
- дисперсия (
) - представляет собой средний квадрат отклонений индивидуальный значений признака от их средней величины.
- в случае отсутствия частот
- в случае наличия частот
- среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от из средней:
или 
или 
- коэффициент осцилляции
,
характеризует отклонение крайних значений признака от среднего значения.
- относительное линейное отклонение
,
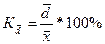характеризует отклонение среднего линейного отклонения от средней.
- коэффициент вариации
,
если V>33 %, статистическая совокупность является неоднородной, т. е. средняя нетипична и необъективна.
Ряд динамики – это данные, расположенные в хронологической последовательности. Ряд динамики состоит из двух элементов:
1. моменты или периоды времени, к которым относятся приводимые статистические данные;
2. статистический показатель, характеризующий изучаемый объект (уровень ряда).
Для характеристики особенностей и закономерностей развития изучаемого объекта рассчитывается система показателей:
- базисные и цепные показатели;
- абсолютные, относительные и средние показатели динамики.
Базисные показатели характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i - го) периода.
Цепные показатели характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
Абсолютные показатели ряда динамики:
- абсолютный прирост (
) - определяется как разность между двумя уровнями динамического ряда и показывает на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:
а) базисный абсолютный прирост:
= yi – y0;
где yi – уровень сравниваемого периода, y0 – уровень базисного периода
б) цепной абсолютный прирост:
= yi – yi-1;
где yi -1 – уровень непосредственно предшествующего периода.
Относительные показатели ряда динамики:
- темп роста – определяется как отношение двух сравниваемых уровней, выражается в процентах.
а) базисный темп роста
Тр = 
б) цепной темп роста
Тр = 
- темп прироста – показывает на сколько процентов уровень данного периода больше (меньше) базисного уровня.
Рассчитывается двояко:
1) как отношение абсолютного прироста к уровню, принятому за базу сравнения.
Тn = 
или Тn = 
2) как разность между темпом роста (в %) и 100%
Тn = Тр – 100%
- абсолютное значение 1 % прироста – рассчитывается как отношение абсолютного прироста к темпу прироста (в %) за тот же период времени
Ai =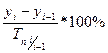 
или Ai =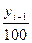 
Средние показатели:
- средний уровень ряда (
)
Метод расчета среднего уровня ряда динамики зависит от вида временного ряда.
Для интервального ряда динамики:
,
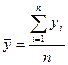где n – число уровней ряда.
Для моментного ряда динамики:
а) моментный ряд с равными промежутками времени
,
где n – число дат (моментов времени)
б) моментный ряд с неравными промежутками времени
,
где ti – количество дней (месяцев) между смежными датами.
- Средний абсолютный прирост (
) – рассчитывается как средняя арифметическая абсолютных приростов за отдельные промежутки времени
,
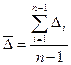где n – число уровней ряда
- абсолютные изменения по сравнению с предшествующим уровнем.
- средний темп роста (
р) – вычисляется по формуле средней геометрической из показателей темпов роста за отдельные периоды
или
,
где Тр1,… Трn-1 – темпы роста по сравнению с уровнем предшествующего периода; n – число уровней ряда.
- Средний темп прироста ( пр) – определяется как разность между средним темпом роста и 100 % и показывает на сколько процентов в среднем изменяются уровни рассматриваемого ряда динамики
-
пр = р – 100 %
Основная тенденция ряда динамики называется трендом. Выявление основной тенденции ряда динамики или выравнивание ряда динамики осуществляется следующими способами:
а) Метод скользящей средней.
Для определения скользящей средней формируют укрупненные интервалы, состоящие из одинакового числа уровней ряда. Каждый последующий интервал получают, постепенно двигаясь от начального уровня ряда динамики на один уровень. Тогда первый интервал будет включать уровни у1, у2, …, уm; второй – уровни у3, у4, …, уm+1 и т.д. По сформированным укрупненным интервалам определяют сумму значений уровней, на основе которых рассчитывают скользящие средние. Полученная средняя относится к середине укрупненного интервала. Поэтому при сглаживании скользящей средней удобнее укрупненный интервал составлять из нечетного числа уровней ряда (3, 5, 7 уровней).
б) Метод аналитического выравнивания.
Метод используется для того, чтобы представить количественную модель, выражающую общую тенденцию изменений уровней ряда динамики во времени. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной кривой, уровень изучаемого показателя оценивается как функция времени yt = ƒ(t), где yt - уровни ряда динамики, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Наиболее часто используемые трендовые модели для аналитического выравнивания:
Линейная уt = в0 + в1t
Парабола 2-го порядка уt = в0 + в1t + в 2t2
Кубическая парабола уt = в0 + в1t + в 2t2 + в 3t3
Показательная уt = в0 в1 t
Экспоненциальная уt = в0 l в1 t
Гипербола уt = в0 + в1 
Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления, а также анализ графического изображения уровней ряда динамики, либо его сглаженных уровней (метод скользящей средней), в которых случайные и волнообразные колебания в некоторой степени оказываются погашенными.
При выборе вида кривой для выражения ряда динамики возможно также использование метода конечных разностей, заключающегося в следующем:
- если общая тенденция выражается линейным уравнением, то постоянными являются первые разности ∆`i = yi – yi-1, и нулевыми вторыми разностями ∆``i = ∆`i – ∆`i-1;
- если тенденция выражается параболой 2-го порядка, то постоянными являются вторые разности и нулевыми – третьи разности.
В общем виде правило можно сформулировать следующими образом: порядок разностей, остающихся примерно равными друг другу, принимается за степень выравнивания многочлена.
Параметры уравнения рассчитываются по методу наименьших квадратов (МНК). Для прямой система нормальных уравнений имеет вид:
, откуда
во = 
; в1 = 
Для параболы второго порядка:
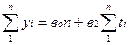
При условии, что ∑ti = 0. Для выполнения этого условия необходимо:
a) в случае нечетного числа уровней ряда. За условно начало отчета (t=0) принимается уровень, находящейся в середине ряда. Даты времени, стоящие выше этого уровня, обозначаются t = -1, -2, -3 и т. д., а ниже -t = +1, +2, +3 и т. д.
b) в случае четного числа уровней ряда. Периоды времени верхней половины ряда (до середины) нумеруются t = -1, -3, -5 и т. д., а нижней - t = +1, +3, +5 и т. д.
Используя полученное уравнение можно строить прогнозы на будущее в развитии изучаемого явления. Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции.
Индексы
Индекс – это относительная величина, которая характеризует изменение во времени или в пространстве уровня изучаемого явления.
Классификация индексов может быть представлена в виде схемы (рис.3).
Рис.3. Классификация индексов
Индивидуальные индексы выражают соотношение отдельных элементов совокупности.
Например, индекс физического объема продукции:
iq = q1 / q 0,
где q0 и q1 – количество произведенной продукции в базисном и отчетном периодах.
Общие индексы показывают соотношение совокупности явлений, состоящих из разнородных, непосредственно несоизмеримых элементов.
Общий индекс состоит из двух элементов – индексируемой (изменяемой) величины и веса - соизмерителя (от влияния которой абстрагируемся).
Наиболее распространенной формой экономических индексов является агрегатная форма индекса, т.е. когда числители и знаменатели представляют собой суммы произведений уровней изучаемого явления.
Общий индекс физического объема продукции рассчитывается по формуле Ласпейреса:
;
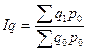Общий индекс цены рассчитывается по формуле Пааше:
.
Общий стоимостной индекс рассчитывается по формуле:
Основное правило индексного анализа:
1. Если оценивается изменение количественных показателей, необходимо использовать для расчетов формулу Ласпейреса (вес – соизмеритель фиксируется на уровне базисного периода).
2. Если оценивается изменение качественных показателей, необходимо использовать формулу Пааше (вес-соизмеритель фиксируется на уровне отчетного периода).
Агрегатные индексы цен, физического объема продукции и товарооборота могут быть вычислены при условии, если известны индексируемые величины и веса. Но в ряде случаев не располагают необходимыми данными, поэтому используют среднеарифметический и среднегармонический индексы.
Среднеарифметический индекс физического объема:
;
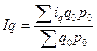Среднегармонический индекс цены:
.
В ряде случаев приходится изучать динамику общественных явлений, уровни которых выражены средними величинами (средней ценой, средней себестоимостью и т.д). Динамика средних показателей зависит от одновременного изменения вариантов, из которых формируются средние, и изменения удельных весов этих вариантов, т.е. от структуры изучаемого явления. Изучение совместного действия указанных факторов на общее изменение динамики среднего уровня явления, а также роли влияния каждого фактора в отдельности в общей динамике средней проводится в статистике с помощью индекса фиксированного состава, индекса переменного состава и индекса структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующее изменение индексируемого (осредняемого) показателя. Индекс переменного состава имеет следующий вид:
Величина этого индекса характеризует изменение средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного (фиксированного) состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя (х) у единиц совокупности. В общем виде он может быть записан следующим образом:
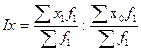
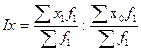
Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:
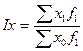
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d). Система взаимосвязанных индексов при анализе динамики среднего уровня качественного показателя имеет вид:
Ixср=Iх * Iстр
В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности (d = f/Sf), которые отражают изменения в структуре изучаемой совокупности.
Аналогично приведенным формулам строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производительности труда, оплаты труда и т.д.
