Лекция №2. 1.3. Решение системы линейных уравнений с помощью матриц

Рассмотрим систему линейных уравнений с многими переменными:

, (5)

где a_ij - коэффициенты при неизвестных х_i; bi -свободные члены;

индексы: i = 1,2,3…m - определяют номер уравнения и j = 1,2,3...n - номер неизвестного.

Определение: Решением системы уравнений (5) называется совокупность n чисел (х₁₀, х₂₀,….х_n0), при подстановке которых в систему все уравнения обращаются в верные числовые тождества.

Определение: Система уравнений называется совместной, если она имеет хотя бы одно решение. Совместная система называется определенной, если она имеет единственное решение (х₁₀, х₂₀,….х_n0), и неопределенной, если таких решений несколько.

Определение: Система называется несовместной, если она не имеет решения.

Определение: Таблицы, составленные из числовых коэффициентов (a_ij) и свободных членов (bi) системы уравнений (5), называются матрицей системы (А) и расширенной матрицей (А₁), которые обозначаются в виде:

А= 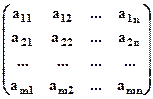и А₁ = .

Определение: Матрица системы А, имеющая неравное число строк и столбцов (n≠m), называется прямоугольной. Если число строк и столбцов совпадает (n=m), то матрица называется квадратной.

Если в системе число неизвестных равно числу уравнений (n=m), то система имеет квадратную матрицу n-го порядка.

Выделим в матрице А k -произвольных строк и k -произвольных столбцов (k£m, k£n).

Определение: Определитель k- порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k- порядка матрицы А.

Рассмотрим всевозможные миноры матрицы А. Если все миноры (k+1)-порядка равны нулю, а хотя бы один из миноров k -порядка не равен нулю, то говорят, что матрица имеет ранг равный k.

Определение: Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Ранг матрицы обозначается через r(A).

Определение: Всякий отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным.

Определение: Если для двух матриц А и В их ранги совпадают r(A)= r(В), то эти матрицы называются эквивалентными и обозначаются А ~ В.

Ранг матрицы не изменится от элементарных, эквивалентных преобразований, которые включают:

1. Замену строк столбцами, а столбцов - соответствующими строками;

2. Перестановку строк или столбцов местами;

3. Вычеркивание строк или столбцов, все элементы которых равны нулю;

4. Умножение или деление строки или столбца на число, отличное от нуля;

5. Прибавление или вычитание элементов одной строки или столбца из другой, умноженной на любое число.

При определении ранга матрицы используют эквивалентные преобразования, с помощью которых исходную матрицу приводят к ступенчатой (треугольной) матрице.

В ступенчатой матрице под главной диагональю располагаются нулевые элементы, причем первый ненулевой элемент каждой её строки, начиная со второй, расположен правее первого неравного нулю элемента предыдущей строки.

Отметим, что ранг матрицы равен числу ненулевых строк ступенчатой матрицы.

Например, матрица А= ~ - ступенчатого вида и её ранг равен числу ненулевых строк матрицы r(A)=3. Действительно, все миноры 4-го порядка с нулевыми элементами 4-ой строки равны нулю, а миноры 3-го порядка отличны от нуля. Для проверки вычислим определитель минора первых 3-х строк и3-х столбцов:

М=

Любую матрицу можно привести к ступенчатой путем обнуления элементов матрицы под главной диагональю с помощью элементарных действий.

Вернемся к исследованию и решению системы линейных уравнений (5).

Важную роль в исследовании систем линейных уравнений играет Теорема Кронекера-Капели. Сформулируем эту теорему.

Теорема Кронекера-Капели: Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы А₁, т.е. r(A)=r(A₁). В случае совместности система является определенной, если ранг матрицы системы равен числу неизвестных, т.е. r(A)=r(A₁)=n и неопределенной, если этот ранг меньше числа неизвестных, т.е. r(A)= r(A₁)<n.

Пример. Исследовать систему линейных уравнений:

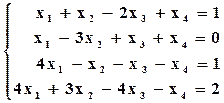
Решение:

Определим ранги матрицы системы А и расширенной матрицы А₁. Для этого составим расширенную матрицу А₁ и приведем её к ступенчатому виду.

При приведении матрицы выполним следующие действия:

1) вычтем из 2-ой строки 1-ю строку;

2) вычтем из 3 и 4 строк 1-ю строку, умноженную на 4;

3) умножим 4-ю строку на (-1) и поменяем местами со 2-ой строкой;

4) сложим 3 и 4 строки со 2-й строкой, умноженной соответственно на 5 и 4;

5) вычитаем из 4-ой строки 3-ю и вычеркиваем 4-ю строку с нулевыми элементами.

А₁= ~ ~ ~

~ ~ ~

В результате выполненных действий получили ступенчатую матрицу с тремя ненулевыми строками как в матрице системы (до черты), так и в расширенной матрице. Откуда видно, что ранг матрицы системы равен рангу расширенной матрицы и равен 3, но меньше числа неизвестных (n=4).

Ответ: т.к. r(A)=r(A₁)=3<n=4, то согласно теореме Кронекера-Капели система совместна, но не определена, имеет бесконечное множество решений.

В связи с тем, что ранг матриц удобно определять путем приведения их к ступенчатому виду, рассмотрим способ решения системы линейных уравнений методом Гаусса.

метод Гаусса

Сущность метода Гаусса заключается в последовательном исключении неизвестных путем приведения к ступенчатому виду расширенной матрицы А₁, которая включает до черты матрицу системы А. При этом одновременно определяются ранги матриц А, А₁ и проводится исследование системы по теореме Кронекера-Капели. На последнем этапе решают систему уравнений ступенчатого вида, делая подстановки снизу вверх найденных значений неизвестных.

Рассмотрим применение метода Гаусса и теоремы Кронекера-Капели на примере.

Пример. Решить систему методом Гаусса:

Решение:

Определим ранги матрицы системы А и расширенной матрицы А₁. Для этого составим расширенную матрицу А₁ и приведем её к ступенчатому виду. При приведении выполним следующие действия:

1) вычтем из 2-ой строки 1-ю строку;

2) вычтем из 3-ей строки 1-ю строку, умноженную на 2;

3) разделим 2-ю строку на (-2),а 3-ю строки умножим на (-1) и поменяем их местами.

А₁= ~ ~ ~

Получили ступенчатую матрицу, у которой число строк равно 3, причем у матрицы системы (до черты) также нет нулевых сток. Следовательно, ранги матрицы системы и расширенной матрицы равны 3 и равны числу неизвестных, т.е. r(A)=r(A₁)=n=3.. Согласно теореме Кронекера-Капели система совместна и определена, имеет единственное решение.

В результате преобразования матрицы А₁, обнуляя коэффициенты при неизвестных, последовательно исключили их из уравнений и получили ступенчатую (треугольную) систему уравнений:

↔ ↔

Двигаясь последовательно снизу вверх, подставляя решение (х₃=1) из третьего уравнения во второе, а решения (х₂=1, х₃=1) из второго и третьего уравнений в первое, получим решение системы уравнений: х₁=1,х₂=1, х₃=1.

Проверка: ↔ Ответ: (х₁=1,х₂=1, х₃=1).

метод Жордано-Гаусса

Данную систему можно решить усовершенствованным методом Жордано-Гаусса, который заключается в том, что матрицу системы А в расширенной матрице (до черты) приводят к единичной матрице: Е= с единичными диагональными и нулевыми недиагональными элементами и получают сразу решение системы без дополнительных подстановок.

Решим рассмотренную выше систему методом Жордано-Гаусса. Для этого преобразуем полученную ступенчатую матрицу в единичную, выполнив следующие действия:

1) вычтем из 1-ой строки 2-ю строку;

2) сложим с 1-ой строкой 3-ю строку, умноженную на 3;

3) вычтем из 2-ой строки 3-ю строку, умноженную на 4.

А₁₌ ~ ~

Исходная система уравнений свелась к системе: 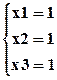, которая и определяет решение.

 

основные действия с матрицами

Пусть даны две матрицы: А= B= .

1. Матрицы равны А=В, если равны их одноименные элементы: a_ij=b_ij

2. Суммой (разностью) матриц (А ± В) называется матрица, определяемая равенством: А±В= ± = .

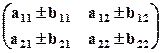При суммировании (вычитании) матриц складываются (вычитаются) их одноименные элементы.

3. Произведением числа k на матрицу A называется матрица, определяемая равенством: kA=k = .

При умножении матрицы на число умножаются на это число все элементы матрицы.

4. Произведением матриц АВ называется матрица, определяемая равенством:

АВ= * = .

При умножении матриц элементы строк первой матрицы умножаются на элементы столбцов второй матрицы и суммируются, причем элемент матрицы-произведения, стоящий в i- й строке и j- м столбце, равен сумме произведений соответственных элементов i- й строки первой матрицы и j- м столбца второй матрицы.

При умножении матриц в общем случае переместительный закон не действует, т.е. АВ≠ВА.

5. Транспонированием матрицы А называется действие, приводящее к замене строк столбцами, а столбцов - соответствующими строками.

Матрица А^Т = называется транспонированной матрицей для матрицы А= .

Если определитель матрицы А не равен нулю (Δ≠0), то такую матрицу называют невырожденной. Для всякой невырожденной матрицы А существует обратная матрица А^-1, для которой выполняется равенство: А^-1 А= А А^-1=Е, где Е= - единичная матрица.

6. Обращением матрицы А называется такие действия, при которых получается обратная матрица А^-1

При обращении матрицы А выполняются следующие действия:

1. Вычисляется определитель матрицы Δ≠0;

2. Для каждого элемента a_ij путем вычеркивания i-строки и j-столбца определяются миноры Mij и вычисляются их алгебраические дополнения Aij==(-1)^I+j Mij

3. Cоставляется матрица из алгебраических дополнений (Aij) и транспонируется (Aij)^Т.

4. Составляется обратная матрица по формуле:

А^-1= =

матричный метод решения системы линейных уравнений с использованием обратной матрицы

Рассмотрим систему линейных уравнений c n неизвестными, имеющей вид:

(6)

Составим квадратную матрицу системы: А= .

Таблица чисел, состоящая только из одного столбца называется матрицей-столбцом или вектором-столбцом.

Введем матрицы-столбцы для неизвестных и свободных членов:

Х= .

Используя основные действия над матрицами, систему линейных уравнений (6) можно представить в матричном виде: А*Х = В (7).

Так, для системы с двумя неизвестными матричный вид будет:

А*Х=В Þ * Þ

Матричное представление системы позволяет непосредственно получить её решение с использованием обратной матрицы.

Действительно, умножим обе части матричного уравнения (7) на обратную матрицу А^-1, получим: А^-1АХ= А^-1В. Учитывая, что А^-1А=Е - единичная матрица и Е*Х=Х, окончательно получим решение системы линейных уравнений в матричном виде: Х=А^-1*В – это формула решения системы линейных уравнений матричным методом с помощью обратной матрицы.

Пример: Решить систему уравнений матричным методом:

Решение: 1)Составим матрицу системы: А= ;

2)Вычислим определитель системы D:

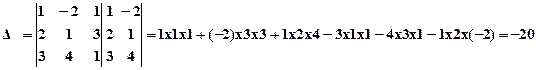
3) Вычислим алгебраические дополнения матрицы системы:

А₁₁=(-1)² =1-12= -11; А₁₂=(-1)³ =-2+9=7 А₁₃=(-1)⁴ =8-3=5

А₂₁=(-1)³ =2+4=6 А₂₂=(-1)⁴ =1-3=-2 А₂₃=(-1)⁵ 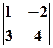=-4-6=-10

А₃₁=(-1)⁴ 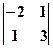=-6-1=-7 А₃₂=(-1)⁵ =-3+2=-1 А₃₃=(-1)⁶ =1+4=5

4) Составим обратную матрицу:

А^-1= = =

5) Находим матрицу-столбец решений по формуле: Х=А^-1В

= * =

6) Выписываем решение системы: х₀=0; у₀=-1;z₀=2

Проверка: (верно).

Ответ: (х₀=0; у₀=-1;z₀=2) – координаты точки пересечения плоскостей

Контрольные вопросы.

1.Минор k-го порядка матрицы. Базисный минор матрицы. Ранг матрицы и его свойства. Теорема о ранге матрицы. Вычисление ранга.

2. Матричные метод решения системы линейных уравнений.

3. Решения системы линейных уравнений методом Гаусса. Квивалентные преобразования систем. Базисные и свободные неизвестные. Критерий совместности системы линейных уравнений.