Дифференцирование функции – это означает нахождение её производной.

Лекция №6

4.4. Производная функции

Переходим к дифференциальному исчислению. Дифференциальное исчисление основывается на понятии производной функции.

Введем понятие производной функции. Пусть на некотором множестве D задана непрерывная функция у = f(х). Возьмем произвольную точку х из этого множества (хÎD) и дадим аргументу приращение х. Причем так, чтобы (х+ х)ÎD При этом функция получит приращение: .

Определение: Производной функции у = f(х) называется предел отношения приращения функции к приращению аргумента , когда приращение аргумента стремится к нулю .

Производная обозначается: .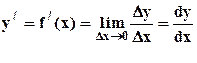

Если функция у = f(x) имеет конечную производную в каждой точке множества D, то производная является также функцией от х. Название производной можно рассматривать как функцию, произведенную от исходной функции у = f(x).

геометрический и физический смысл производной

Геометрически производная определяет угловой коэффициент касательной к графику функции у=f(x), т.е. .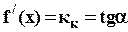

Пусть на графике функции у = f(x) задана точка М₁(х₁,у₁). Проведем касательную K и нормаль N к графику функции в заданной точке. Нормаль – это прямая перпендикулярная к касательной.

Угловой коэффициент касательной равен значению производной в заданной точке , а угловой коэффициент нормали из условия N┼K равен .

Тогда можно записать уравнения касательной и нормали к графику функции в заданной точке М₁(х₁,у₁), используя уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом:

- ур. касательной; - ур. нормали.

Физический смысл производной заключается в том, что она определяет мгновенную скорость движения.

Пусть материальная точка двигается по закону у = f(t), где у - пройденный путь за время t. Тогда скорость движения в момент времени t = t₀, будет равна:

.

Ниже будет дан пример расчета скорости и ускорения, исходя из физического смысла первой и второй производных.

4.5. дифференцирование функций

Определение: Функция у = f(x) называется дифференцируемой на множестве D, если в каждой точке этого множества существует конечная её производная, т.е. для каждого хÎD существует конечный предел .

Дифференцирование функции – это означает нахождение её производной.

Теорема. Для того, чтобы функция у = f(x) была дифференцируемой на множестве D необходимо и достаточно, чтобы в каждой точке хÎD этого множества приращение функции ∆у можно было представить в виде: ∆у=А*∆х+α(∆х)*∆х, где А – множитель, который определяется значением производной в точке х: А=f^/(x); α(∆х) – б.малая функция при ∆х®0.

Действительно, если ∆у=А*∆х+α(∆х)*∆х, то существует конечный предел:

.

дифференциал функции

Определение: Дифференциалом функции у=f(x) называется главная линейная часть приращения функции, которая обозначается в виде:

dy= А*∆х=f ^/(x)* ∆х.

Если возьмём линейную функцию у=х, то дифференциал этой функции будет равен: dх=(x)^/* ∆х=1*∆х=∆х или dх =∆х, т.е. дифференциал аргумента равен его приращению.

Тогда дифференциал любой функции будет равен: dy=f ^/(x)*dх. Откуда производную можно представить в виде отношения дифференциала функции к дифференциалу аргумента: .

Используя обозначение дифференциала, приращение функции можно представить в виде: ∆у=dy+α(∆х)*∆х. Второй нелинейный член приращения: α(∆х)*∆х является б.малой величиной более высокого порядка, чем ∆х и ввиду его малости можно отбросить из выражения. Тогда приращение функции приблизительно равно её дифференциалу: ∆у» dy = f^/(x)* ∆х.

Если представить приращение функции в виде: ∆у=f(x+∆х)-f(x)» f^/(x)* ∆х, тогда можно записать f(x+∆х)»f(x) + f^/(x)* ∆х. Данная формула используется для приближенного расчета значения функции в точке x+∆х по известному значению в точке х.

Теорема о связи между дифференцируемостью и непрерывностью функции. Если функция y=f(x) является дифференцируемой в точке х, то в этой точке она непрерывна.

Отметим, что всякая дифференцируемая на множестве D функция является непрерывной на этом множестве. Однако обратное утверждение не верно – не всякая непрерывная функция является дифференцируемой.

Таблица производных элементарных функций

1. С /= 0,гдеС =const 2. , где показатель -число 3. 4. ,где е = 2,71... 5. 6. 7.

8. 9. 10. 11. 12. 13. 14.

Основные правила дифференцирования

Пусть даны две дифференцируемые функции: f(x) и j(x).

1. Правило дифференцирования суммы, разности функций:

;

2. Правило дифференцирования произведения:

;

3. Правило дифференцирования частного (дроби):

.

4. Правило дифференцирования сложной функции.

Пусть дана функция у = f(u), где u = u(x) - промежуточный аргумент или промежуточная функция. Тогда у=f(u(x)) называется сложной функцией. Производная от сложной функции вычисляется по формуле: .

Пример: , т. к. (sin u)^/=(sinu)^/* u^/ где u = x³.

4.7. Исследование функций с помощью производных

4.7.1. основные теоремы дифференциального исчисления

Основные теоремы дифференциального исчисления лежат в основе исследования функций с помощью производных.

Теорема Ферма. Если дифференцируемая на отрезке [а,b] функция y=f(x) достигает своего наибольшего или наименьшего значения внутри отрезка в некоторой точке х=c, то производная в этой точке равна нулю: f ^/(c) = 0.

Геометрический смысл теоремы Ферма заключается в том, что если дифференцируемая на отрезке [а,b] функция y=f(x) внутри отрезка в точке х=c имеет наибольшее или наименьшее значение, то касательная к графику функции в этой точке параллельна оси Ох, т.к. угловой коэффициент касательной, который определяется значением производной в этой точке равен нулю: к_к=f ^/(c)=0.

Теорема Ролля. Если дифференцируемая на отрезке [а,b] функция y=f(x) принимает на концах отрезка равные значения f(a)=f(b), то внутри отрезка [а,b]существует точка х=с, в которой производная равна нулю: f ^/(c) = 0.

Геометрический смысл теоремы Ролля заключается в том, что у графика дифференцируемой на отрезке [а,b] функция y=f(x), принимающей на концах этого отрезка равные значения f(a)=f(b), существует такая точка х=с внутри отрезка, в которой касательная к графику функции в этой точке параллельна оси Ох.

Теорема Лагранжа. Если функция y=f(x) дифференцируема на отрезке [а,b], то внутри этого отрезка существует такая точка х=с, в которой производная равна

f ^/(c) = .

Геометрический смысл теоремы Лагранжа заключается в том, что у графика дифференцируемой на отрезке [а,b] функция y=f(x), существует такая точка х=с внутри отрезка [а,b], в которой касательная к графику функции в этой точке параллельна секущей, соединяющей график на концах отрезка.

Правило Лопиталя. Предел отношения двух б.малых или б.больших функций в точке х=х₀ или на бесконечности при равен пределу отношения их производных:

Правило Лопиталя используется для вычисления пределов при раскрытии неопределенностей типа: .

Примеры. Вычислить пределы:

1. ;

2. .

4.7.2.Признак монотонности функций

Определение: Функция f(x) называется монотонной на интервале, если она на нем или только возрастает, или только убывает.

Если функция монотонно возрастает на интервале, то большему значению аргумента х₂>x₁, соответствует большее значение функции: f(x₂)>f(x₁).

Если функция монотонно убывает на интервале, то большему значению аргумента х₂>x₁, соответствует меньшее значение функции: f(x₂)<f(x₁).

На рисунке на интервале функция монотонно возрастает, а на интервале монотонно убывает.

Введем обозначения Dх = х₂ - х₁ - приращение аргумента и приращение функции: у = f(x₂) - f(x₁). Для возрастающей функции приращения аргумента и функции имеют одинаковые знаки, а следовательно, отношение >0. Для убывающей функции приращения аргумента и функции имеют противоположные знаки, а следовательно, отношение < 0. Так как первая производная функции равна , то по знаку производной можно определять участки возрастания и убывания функции.

Необходимый и достаточный признак монотонности функции

Теорема. Если функция у=f(x) дифференцируема на интервале и ее производная положительна у¢>0, то функция на этом интервале монотонно возрастает, а если производная отрицательна у¢<0, то функция на интервале монотонно убывает.

Свяжем это с геометрическим смыслом первой производной, которая определяет угловой коэффициент касательной. Для возрастающей функции угол наклона касательной острый 0⁰<a<90⁰, а следовательно, у^/=tga>0. Для убывающей функции этот угол тупой 90⁰<a<180⁰, у^/=tga<0.

Отметим, что если в точках первая производная равна нулю или не существует, то в этих точках функция не возрастает и не убывает. Здесь возможны:

· точки перегиба, в которых выпуклость графика функции сменяется вогнутостью или наоборот;

· точки локального экстремума, в которых участок возрастания функции сменяется участком убывания или наоборот.

Определение: Точки, в которых первая производная либо равна нулю, либо не существует, называются критическими точками I рода.

4.7.3. Локальные экстремумы функций

Определение: Точка х₀ называется точкой локального максимума (или минимума) функции, если в некоторой окрестности точки х₀ функция принимает наибольшее (или наименьшее) значение, т.е. для всех х из некоторой окрестности точки х₀ выполняется условие f(x) f(x₀) (или f(x) f(x₀)).

Точки локального максимума или минимума объединены общим названием - точками локального экстремума функции.

Отметим, что в точках локального экстремума функция достигает своего наибольшего или наименьшего значения лишь в некоторой локальной области. Возможны случаи, когда по значению у_max у_min.

Необходимый признак существования локального экстремума функции

Теорема. Если непрерывная функция у = f(x) имеет в точке х₀ локальный экстремум, то в этой точке первая производная либо равна нулю, либо не существует, т.е. локальный экстремум имеет место в критических точках I рода.

В точках локального экстремума либо касательная параллельна оси 0х, либо имеются две касательные (см. рисунок). Отметим, что критические точки являются необходимым, но недостаточным условием локального экстремума. Локальный экстремум имеет место только в критических точках I рода, но не во всех критических точках имеет место локальный экстремум.

Например: кубическая парабола у = х³, имеет критическую точка х₀=0, в которой производная у^/(0)=0, но критическая точка х₀=0 не является точкой экстремума, а в ней имеет место точка перегиба (см. ниже).

Достаточный признак существования локального экстремума функции

Теорема. Если при переходе аргумента через критическую точку I рода слева направо первая производная у ^/ (x)

1) меняет знак с “+” на “-”, то непрерывная функция у(х) в этой критической точке имеет локальный максимум;

2) меняет знак с “-” на “+”, то непрерывная функция у(х) имеет в этой критической точке локальный минимум

3) не меняет знак, то в этой критической точке нет локального экстремума, здесь имеет место точка перегиба.

Для локального максимума область возрастания функции (у^/ 0) сменяется на область убывания функции (у^/ 0). Для локального минимума область убывания функции (у^/ 0) сменяется на область возрастания функции (у ^/ 0).

Пример: Исследовать функцию у = х³ + 9х² + 15х - 9 на монотонность, экстремум и построить график функции.

Решение:

1) Найдем критические точки I рода, определив производную (у^/) и приравняв ее нулю: у^/ = 3х² + 18х + 15 =3(х² + 6х + 5) = 0

Решим квадратный трехчлен с помощью дискриминанта: х² + 6х + 5 = 0 (а=1, в=6, с=5) D= , , х_1к = -5, х_2к = -1.

2) Разобьем числовую ось критическими точками на 3 области и определим в них знаки производной (у^/). По этим знакам найдем участки монотонности (возрастания и убывания) функций, а по изменению знаков определим точки локального экстремума (максимума и минимума).

Результаты исследования представим в виде таблицы, из которой можно сделать следующие выводы:

1. На интервале у ^/(-10)> 0 функция монотонно возрастает (знак производной у¢ оценивался по контрольной точке х = -10, взятой в данном интервале);

2. На интервале (-5; -1) у ^/(-2)< 0 функция монотонно убывает (знак производной у¢ оценивался по контрольной точке х = -2, взятой в данном интервале);

3. На интервале у ^/(0)> 0 функция монотонно возрастает (знак производной у¢ оценивался по контрольной точке х = 0, взятой в данном интервале);

1. При переходе через критическую точку х_1к= -5 производная меняет знак с "+" на "-", следовательно эта точка является точкой локального максимума

(y_max(-5) = (-5)³+9´(-5)² +15´(-5)-9=-125 + 225 - 75 - 9 =16);

2. При переходе через критическую точку х_2к= -1 производная меняет знак с "-" на "+", следовательно эта точка является точкой локального минимума

(y_min(-1) = -1 + 9 - 15 - 9 = - 16).

х -5 (-5; -1) -1

y ^/ + 0 - 0 +

Y 16 -16

max min

3) Построение графика выполним по результатам исследования с привлечением дополнительных расчетов значений функции в контрольных точках:

· строим прямоугольную систему координат Оху;

· показываем по координатам точки максимума (-5; 16) и минимума (-1;-16);

· для уточнения графика рассчитываем значение функции в контрольных точках, выбирая их слева и справа от точек максимума и минимума и внутри среднего интервала, например: у(-6)=(-6)³ +9´(-6)²+15´(-6)-9=9; у(-3)=(-3)³+9´(-3)²+15´(-3)-9=0;

у(0)= -9 Þ (-6;9); (-3;0) и (0;-9) – расчетные контрольные точки, которые наносим для построения графика;

· показываем график в виде кривой выпуклостью вверх в точке максимума и выпуклостью вниз в точке минимума и проходящей через расчетные контрольные точки.

4.7.4. Выпуклость, вогнутость графика функции и точки перегиба

Определение: График дифференцируемой на интервале (a;b) функции называется выпуклым (или вогнутым), если он расположен ниже (выше) любой своей касательной на этом интервале.

Так график кубической параболы у=х³ на интервале выпуклый и лежит ниже своих касательных, а на интервале вогнутый и лежит выше своих касательных.

Отметим, что выпуклость и вогнутость графика функции можно определять по знаку её второй производной. Для кубической параболы у=х³ график на интервале выпуклый, а вторая производная на этом интервале отрицательна у^//=(3x²)^/=6x<0(при x<0). На интервале её график вогнутый, а вторая производная на этом интервале положительна у^//=6x>0(при x>0). Это связано с тем, что вторая производная определяет поведение первой производной. Для выпуклого участка угловой коэффициент касательной, который определяется первой производной, убывает, а следовательно вторая производная отрицательна, а для вогнутого участка наоборот угловой коэффициент касательной возрастает, а следовательно вторая производная положительная.

 

 

необходимыЙ и достаточныЙ признак выпуклости и вогнутости

Теорема. Если на интервале (а;b) вторая производная непрерывной функции положительна у^//>0, то график функции вогнутый, а если вторая производная отрицательна у^//<0, то график функции выпуклый.

Определение: Точка, отделяющая выпуклую часть от вогнутой, называется точкой перегиба.

Необходимый признак существования точек перегиба

Теорема. Если непрерывная функция y=f(x) имеет точку перегиба х_п, то в этой точке вторая производная равна нулю (у^//=0) или не существует.

Определение: Точки, в которых вторая производная равна нулю (у^//=0) или не существует называются критическими точками второго рода.

Согласно теоремы точки перегиба бывают только в критических точках второго рода, но не во всех в критических точках второго рода имеют место точки перегиба.

Достаточный признак существования точек перегиба

Теорема. Если при переходе аргументом через критическую точку второго рода х_п вторая производная меняет знак, то эта критическая точка является точкой перегиба.

Так кубическая парабола у=х³ имеет точку перегиба х_п=0, в которой её вторая производная у^//=6х_п=0 и при переходе через эту точку вторая производная меняет знак с «-» на «+».

4.7.5. асимптоты графиков функций

При исследовании поведения функций на бесконечности при х®∞ или вблизи точек бесконечного разрыва второго рода, когда у®∞ часто оказывается, что график функции неограниченно близко приближается к некоторой прямой.

Определение: Прямые к которым неограниченно близко приближаются графики функций называются асимптотами.

Асимптоты бывают трех видов: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты имеют место в точках бесконечного разрыва второго рода, когда пределы в этих точках равны бесконечности.

Определение: Прямая х=а называется вертикальной асимптотой графика функции у=f(x), если стремится к бесконечности хотя бы один из пределов: правый или левый .

Вертикальные асимптоты имеют место, когда функция неопределена в точке при делении на ноль.

Пример. Функция 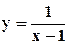неопределена при

х-1=0 или х=1. В этой точке функция терпит бесконечный разрыв второго рода, т.к. -левый предел; -правый предел. Прямая х=1 является вертикальной асимптотой.

Здесь же отметим, что на бесконечности при х®±∞ эта функция стремится к нулю: у=f(x) ® 0, т.к. =0. Горизонтальная прямая у=0, к которой стремится функция на бесконечности называется горизонтальной асимптотой.

Определение: Прямая у=b называется горизонтальной асимптотой графика функции у=f(x) при х®±∞, если равен числу b любой из пределов: .

Отметим, что эти пределы могут быть разными , а следовательно имеют место две горизонтальные асимптоты y=b₁и y=b₂.

Существуют также наклонные асимтоты.

Определение: Прямая у=kx+b называется наклонной асимптотой графика функции y=f(x) при х ®±∞, если равен нулю любой из пределов .

Для отыскания наклонной асимптоты используют следующую теорему.

Теорема. Для того, чтобы график функции y=f(x) имел наклонную асимптоту необходимо и достаточно, чтобы одновременно существовали по два конечных предела .

С помощью этих пределов определяются параметры (k и b) наклонных асимптот. Причем пределы при х® - ∞ и при х® + ∞ вычисляются раздельно, т.к. возможны две разные наклонные асимптоты у=k₁x+b₁ и y= k₂x+b₂.

Отметим, что горизонтальная асимптота у=b является частным случаем наклонной асимптоты, когда .

4.7.6. Общая схема исследования функций и построения графиков

Общая схема исследования функций и построения графиков включает следующие этапы:

1. Находится область определения функции D(y);

2. Находятся точки пересечения графика функции с осями координат: у(0) и у(х)=0 и определяются интервалы знакопостоянства функции;

3. Определяются точки разрыва функции, в которых нарушаются условия непрерывности, и вычисляются односторонние пределы в этих точках;

4. Находятся вертикальные асимптоты в точках бесконечного разрыва, а также наклонные и горизонтальные асимптоты при х® ± ∞;

5. Находятся критические точки первого рода, в которых первая производная равна нулю или не существует, и определяются по знаку этой производной интервалы монотонности, а по изменению знака определяются точки локального экстремума;

6. Находятся критические точки второго рода, в которых вторая производная равна нулю или не существует, и определяются по знаку этой производной интервалы выпуклости и вогнутости, а по изменению знака определяются точки перегиба;

7. Строится график функции, используя полученные результаты исследования. При необходимости рассчитывают несколько контрольных значений функции по её формуле.