Розрахункова робота з дисципліни
“Системи обробки сигналів та зображень”
Варіант 2
|
| ||||
Київ – 2012
Зміст:
1. Варіант завдання розрахункової роботи
2. Теоретичні відомості
3. Розрахунок
4.Висновки
Варіант завдання розрахункової роботи
Варіант 2.
2.1 Дискретизовний сигнал 
заданий своїми значеннями у наступній таблиці:
| ||||||||||
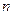
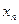
| 0,2 | 0.4 | 0.6 | 0.8 | 1.2 | 1.4 | 1.6 | 1.8 | ||
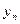
| -0.8 | -0.6 | 0.2 | 0.7 | 0.9 | 1.4 | 0.8 | 0.4 | 0.1 | -0.2 |
Провести згладжування (апроксимацию) даних за допомогою полінома
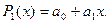Вирахувати значення різниць (відхилень) між вихідними і згладженими даними, знайти максимальне по модулю значення їх різниці та суму квадратів відхилень між вихідними та згладженими даними. Подати усі вихідні дані та результати обчислювань у відповідній табличній та графічній формі.
2.2 Розглядається задача відновлення дискретизованого часового сигнала
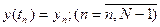по його заданому спектру (амплітудному 
та фазовому 
наступного вигляду
 гц
| …. | …. | … | … | … | |||||||||
|
| ||||||||||||||
 град
| -180 | -90 | -90 | -180 |
Дати графічну інтерпретацію заданого спектру у вигляді відповідного графіка і знайти аналітичний вираз для часового сигналу 
, визначивши його період дискретизації 
, інтервал визначення,число дискрет N і частоту дискретизації 
.
Теоретичні відомості
Лінійне поліноміальне згладжування.
Метод ковзаючого середнього має один суттєвий недолік – зростаюча втрата даних при збільшені числа проходів згладжування. Цей недолік можна усунути якщо замість полінома нулевої степені 
використати поліном першої степені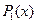 
, який має вже два шуканих коефіцієн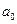та 
та 
; тобто він подається у такому вигляді 
і задає пряму лінію. Знову ж таки вибираємо для побудови цього поліному мінімально можливу кількість даних з вихідного масиву 
- три, записуючи квадратичну міру близькості і поліном у такому вигляді:
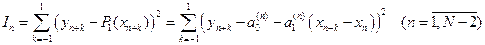(2.1.1)
Оптимальні значення шуканих коефіцієнтів 
на 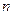-тому кроці згладжування знаходиться із умови екстремуму (мінімуму) міри близькості (2.1.1), тобто:
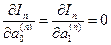
, (2.1.2)
що дає після перетворення таку систему алгебраїчних рівнянь:
(2.1.3)
Припускаючи, що дискрети 
рівновіддалені одна від одної з інтервалом 
, маємо:
,
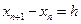а в системі рівнянь (2.1.3) отримуємо такі коефіцієнти:
В результаті система рівнянь (2.1.3) перетворюється в таку:
(2.1.4)
що дає наступний розв’язок:
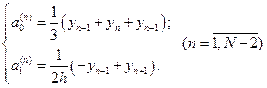(2.1.5)
Оскільки значення згладжених даних тепер розраховуються по поліному 
у точці 
, то 
і у виразі
(2.1.6)
зникає різниця 
і тому залишається тільки 
, тобто необхідно використати тільки коефіцієнт 
, 
, а значить і вирахувати тільки наступне:
(2.1.7)
Якщо поставити за мету не втрачати по два значення – одне на початку, а друге – в кінці масиву даних, то потрібно скористатися повним виразом для поліному з коефіцієнтами при 
і 
, а також 
і 
відповідно, що дає:
(2.1.8)
Підставивши (2.1.5) в (2.1.8) отримуємо таке:
(2.1.9)
