Задача аппроксимации функции. Исследуем объект, работа которого характеризуется показателем Y, на работу объекта оказывает влияние набор факторов Х=(х1, х2,…,хn). Допускается воздействие случайных неконтролируемых факторов e=(e1, e2,…,em) (неучтенные факторы, ошибки измерения).
e
Таблица исходных данных (n-переменных, m –наблюдений)
| Х1 | Х2 | … | Хm | Y |
| х11 | Х12 | X1n | Y1 | |
| Х21 | X22 | X2n | Y2 | |
| . | . | . | ||
| Xn1 | Xn2 | Xnm | Yn |
X
|
Рис. Структура исследуемого объекта
Пример 1 Обрывность=F(влажность, температура, Тексв,…)
|
… Y (обрывность)
хm
Пример 2 Прибыль= F(величина основных фондов, величина оборотных фондов)
Пусть объективно существует зависимость Y=F(X), которая неизвестна, а известны только результаты фактических наблюдений за работой объекта {Xi,Yi}I=1,…n 
, которые представлены в таблице, где Yi= F(Xi) +ei I=1,2…n. Т.к. фактическое значение показателя Yi наблюдается с ошибкой ei (из-за неучтенных факторов и ошибок измерения).
Требуется найти функцию Y = 
(Х), которая наилучшим образом аппроксимирует фактические данные, приближаясь к истинной функции: 
= F(Х)
В зависимости от вида функции F(X) модели делятся на линейные и нелинейные. В зависимости от количества включенных в модель факторов модели делятся на однофакторные и многофакторные.
Рассмотрим задачу построения регрессионной зависимости на примере однофакторной линейной модели.
Пусть объект описывается показателем Y и на него оказывает влияние один фактор X, истинная функция Y =F(X)+e задана таблицей значений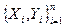 
. Требуется построить аппроксимацию 
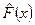, которая хорошо приближается к истинной функции F(X) в смысле минимального значения суммы квадратов отклонений истинных значений Yi от линии регрессии.
Например, нас интересует как зависит товарооборот от вложенных затрат на рекламу (y – объем товарооборота, x – затраты на рекламу)
- истинная функция y =F(x) не известна, а известны фактические значения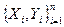 
, где Yi= F(Xi) +ei I=1,2…n (n - наблюдений), собранные за некоторый период времени.
Требуется:
- найти приближение к истинной функции F(X) в классе линейных функций, т.е. определить коэффициенты оптимальной линейной зависимости 
= aХ + b на основе фактических данных
- провести анализ полученной зависимости на предмет адекватности исходным данным.
Выдвигаем гипотезу:
переменные связаны линейной зависимостью Y=AX+B+e, т.е. наилучшую аппроксимацию ищем в классе линейных функций:
Одним из методов построения такой аппроксимации является регрессионный анализ, а построенную этим методом функцию называют уравнением регрессии (функцией регрессии).
Регрессионный анализ заключается в определении аналитического выражения связи зависимой случайной величины Y (показателя) с независимыми случайными величинами Х1, Х2,…Хn (факторами). В регрессионном анализе “наилучшим образом”, понимается в смысле минимума суммарной ошибки приближения для заданных исходных (табличных) данных.
Функция регрессии показывает, каково будет в среднем значение переменной Y, если переменные 
примут конкретные значения.
Основной метод, с помощью которого оцениваются неизвестные параметры в регрессионном анализе – метод наименьших квадратов (МНК). МНК – это вычислительная процедура, обеспечивающая минимизацию заданной квадратичной формы при фиксированном множестве исходных данных.
Сочетание МНК с указанными статистическими процедурами и привело к созданию того, что стало называться регрессионным анализом. Постепенно расширилась и область приложений регрессионного анализа
Основные этапы регрессионного анализа
1. Формирование набора исходных данных, характеризующих работу объекта;
2. Предварительный статистический анализ данных. Построение системы показателей и факторов. Выбор типа связи регрессионной зависимости (задание класса функций). Выдвижение гипотезы о типе связи между переменными;
3. Оценивание параметров функции регрессии (МНК);
4. Проверка адекватности построенной зависимости. Проверка выдвинутой гипотезы.
